0 < x < \(\frac { \pi }{ 2 } \), 0 < y < \(\frac { \pi }{ 2 } \)
(x, y) I  கால் பகுதியில் அமைவதால் இவை அனைத்து முக்கோணவியல் விகிதங்களும் மிகையாகும்
= \(\sqrt { { 17 }^{ 2 }-{ 15 }^{ 2 } } \)
= \(\sqrt { 289-225 } \)
= \(\sqrt { 64 } \) = 8
\(\sqrt { { 13 }^{ 2 }-{ 12 }^{ 2 } } \)
= \(\sqrt { 169-144 } \)
= \(\sqrt { 25 } \) = 5

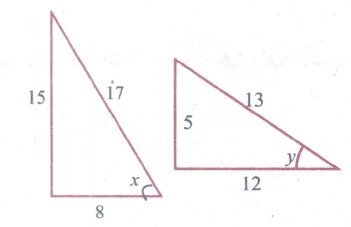
sin x = \(\frac { 15 }{ 17 } \)       sin y = \(\frac { 5 }{ 13 } \)
cos x = \(\frac { 8 }{ 17 } \)       cos y = \(\frac { 12 }{ 13 } \)
tan x =\(\frac { 15 }{ 8 } \)        tan y = \(\frac { 5 }{ 12 } \)
cosec x = \(\frac { 17 }{ 15 } \)    cosec y = \(\frac { 13 }{ 5 } \)     
sec x = \(\frac { 17 }{ 8 } \)      sec y = \(\frac { 13 }{ 12 } \)
cot x = \(\frac { 8 }{ 15 } \)        cot y = \(\frac { 12 }{ 5 } \)
sin (x + y) = sin x cos y + cos x sin y
= \(\frac { 15 }{ 17 } \times \frac { 12 }{ 13 } +\frac { 8 }{ 17 } \times \frac { 5 }{ 13 } \)
= \(\frac { 180 }{ 221 } +\frac { 40 }{ 221 } =\frac { 220 }{ 221 } \)