12th Standard கணிதவியல் Subject Question Paper Software Subscription
QB365 covers complete information about Tamilnadu 12th Standard 2024-2025 கணிதவியல் Subject. Question Bank includes 12th Standard 2024-2025 கணிதவியல்Subject Book back questions, other important questions, Creative questions, Extra questions, PTA questions, Previous Year asked questions and other key points also. All question with detailed answers are readily available for preparing கணிதவியல் question papers.
All Chapters Covered

Create Unlimited Question Papers

Access anywhere anytime

Multiple Pattern Question Papers
Share your Question Paper

Font size, line spacing, watermark etc,
Other Subjects for Tamil Nadu State Board 12th Standard
12th Standard கணிதவியல் Tamil Medium Chapters / Lessons 2024-2025
அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள்
கலப்பு எண்கள்
சமன்பாட்டியல்
நேர்மாறு முக்கோணவியல் சார்புகள்
இரு பரிமாண பகுமுறை வடிவியல் - II
வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்
வகை நுண்கணிதத்தின் பயன்பாடுகள்
வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள்
தொகை நுண்கணிதத்தின் பயன்பாடுகள்
சாதாரண வகைக்கெழுச் சமன்பாடுகள்
நிகழ்தகவு பரவல்கள்
தனிநிலைக் கணிதம்
12th Standard கணிதவியல் Tamil Medium Chapters / Lessons 2024-2025 Syllabus
அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள்
அறிமுகம் - பூச்சியமற்ற கோவை அணியின் நேர்மாறு - ஓர் அணியின் மீதான தொடக்கநிலை உருமாற்றங்கள் - அணிகளின் பயன்பாடுகள்: நேரியச் சமன்பாடுகளின் தொகுப்பிற்கான தீர்வு காணுதல் - நேரியச் சமன்பாடுகளின் தொகுப்பிற்குரிய ஒருங்கமைவுத் தன்மையை தரம் மூலம் காணல்
கலப்பு எண்கள்
கலப்பெண்கள் அறிமுகம் - கலப்பு எண்கள் - கலப்பெண்களின் அடிப்படை இயற்கணிதப் பண்புகள் - ஒரு கலப்பெண்ணின் இணைக் கலப்பெண் - ஒரு கலப்பெண்ணின் மட்டு மதிப்பு - கலப்பெண்களின் வடிவியல் மற்றும் நியமப்பாதை - கலப்பு எண்களின் துருவ வடிவம் மற்றும் யூலரின் வடிவம் - டி மாய்வரின் தேற்றமும் அதன் பயன்பாடுகளும்
சமன்பாட்டியல்
அறிமுகம் - பல்லுறுப்புக் கோவைச் சமன்பாடுகளின் அடிப்படைக் கூறுகள் - வியட்டாவின் சூத்திரங்கள் மற்றும் பல்லுறுப்புக் கோவைச் சமன்பாடுகளை உருவாக்குதல் - பல்லுறுப்புக் கோவைச் சமன்பாடுகளின் கெழுக்களின் பண்புகள் மற்றும் மூலங்களின் பண்புகள் - வடிவியலில் பல்லுறுப்புக் கோவைச் சமன்பாடுகளின் பயன்பாடுகள் - உயர்ப்படி பல்லுறுப்புக் கோவைச் சமன்பாடுகளின் மூலங்கள் - கூடுதல் விவரங்களுடன் கூடிய பல்லுறுப்புக் கோவைகள் - கூடுதல் விவரம் இல்லாத பல்லுறுப்புக் கோவைச் சமன்பாடுகள்
நேர்மாறு முக்கோணவியல் சார்புகள்
அறிமுகம் - சில அடிப்படைக் கருத்துகள் - சைன் சார்பு மற்றும் நேர்மாறு சைன் சார்பு - கொசைன் சார்பு மற்றும் நேர்மாறு கொசைன் சார்பு - தொடுகோட்டுச் சார்பு மற்றும் நேர்மாறு தொடுகோட்டுச் சார்பு - கொசீகண்ட் சார்பு மற்றும் நேர்மாறு கொசீகண்ட் சார்பு - சீகண்ட் சார்பு மற்றும் நேர்மாறு சீகண்ட் சார்பு - கோடான்ஜெண்ட் சார்பு மற்றும் நேர்மாறு கோடான்ஜெண்ட் சார்பு - நேர்மாறு முக்கோணவியல் சார்புகளின் முதன்மை மதிப்பு - நேர்மாறு முக்கோணவியல் சார்புகளின் பண்புகள்
இரு பரிமாண பகுமுறை வடிவியல் - II
அறிமுகம் - வட்டம் - கூம்பு வளைவுகள் - கூம்பு வெட்டு முகங்கள் - கூம்பு வடிவின் துணையலகு வடிவம் - கூம்பு வளைவரையின் தொடுகோடுகள் மற்றும் செங்கோடுகள் - அன்றாட வாழ்வில் கூம்பு வளைவரைகளின் பயன்பாடுகள்
வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள்
அறிமுகம் - வெக்டர்களின் வடிவக் கணித அறிமுகம் - திசையிலிப் பெருக்கல் மற்றும் வெக்டர் பெருக்கல் - திசையிலி முப்பெருக்கல் - வெக்டர் முப்பெருக்கல் - ஜக்கோபியின் முற்றொருமை மற்றும் லாக்ராஞ்சியின் முற்றொருமை - முப்பரிமாண வடிவக் கணிதத்தில் வெக்டர்களின் பயன்பாடு - ஒரு தளத்தின் பல்வேறு வகைச் சமன்பாடுகள் - தளத்தில் ஒரு புள்ளியின் பிம்பம் - ஒரு கோடும் ஒரு தளமும் சந்திக்கும் புள்ளி
Features in Question Paper Preparation software

(or) type Question

Add or Remover

Sub Questions

Adding Notes

Multiple Pattern

All subjects available
How to Create 12th Standard கணிதவியல் Tamil Medium Question Paper
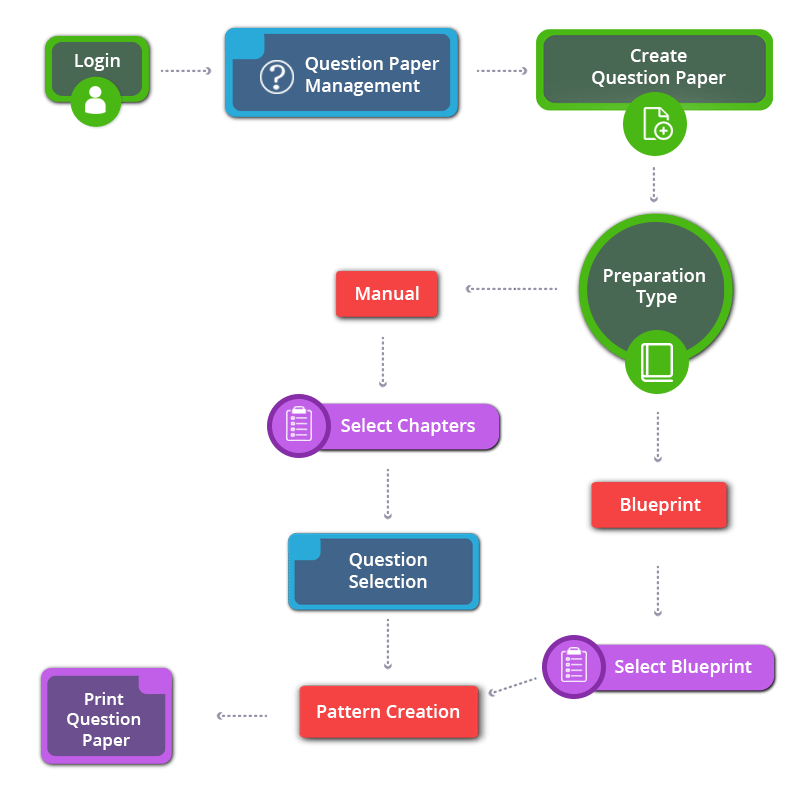

12th Standard கணிதவியல் Tamil Medium Chapters / Lessons 2024-2025
- Covers all chapters
- Unique Creative Questions
- Unlimited Question Paper
- Multiple Patterns & Answer keys
1665
1499



