Represent each of the given relations by (a) an arrow diagram, (b) a graph and (c) a set in roster form, wherever possible.
(i) {(x, y)|x = 2y, x \(\in \) {2, 3, 4, 5}, y \(\in \) {1, 2, 3, 4}
(ii) {(x, y)|y = x + 3, x, y are natural numbers < 10}

An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal squares from the corners and turning up the sides as shown Fig. Express the volume V of the box as a function of x.

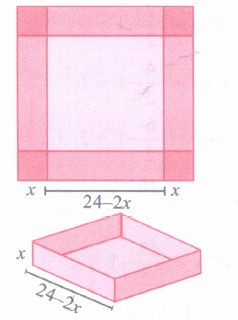
A function f: [-7,6) \(\rightarrow\) R is defined as follows.

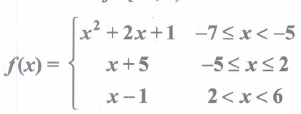
f(-7) - f(-3)

A function f: [-7,6) \(\rightarrow\) R is defined as follows.

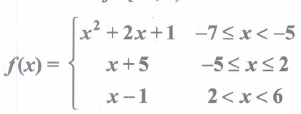
\(\cfrac { 4f(-3)+2f(4) }{ f(-6)-3f(1) } \)

Let A = {1, 2, 3, 4, 5}, B = N and f: A \(\rightarrow\)B be defined by f(x) = x². Find the range of f. Identify the type of function.

Discuss the nature of solutions of the following system of equations
2y + z = 3(-x + 1); -x + 3y - z = -4; 3x + 2y + z = \(-\frac {1}{2}\)

Seven years ago, Varun's age was five times the square of Swati's age. Three years hence Swati's age will be two fifth of Varun's age. Find their present ages.

If \(\triangle\)ABC~\(\triangle\)DEF such that area of \(\triangle\)ABC is 9cm² and the area of \(\triangle\)DEF is 16cm² and BC = 2.1 cm. Find the length of EF

In the given figure AB || CD || EF. If AB = 6cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y can. Final x and y

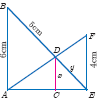
Without using Pythagoras theorem, show that the vertices (1, - 4) , (2, - 3) and (4, - 7) form a right angled triangle.

A circular garden is bounded by East Avenue and Cross Road. Cross Road intersects North Street at D and East Avenue at E. AD is tangential to the circular garden at A(3, 10). Using the figure.

Where does the Cross Road intersect the
(i) East Avenue ?
(ii) North Street ?

A statue 1.6 m tall stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point the angle of elevation of the top of the pedestal is 40°. Find the height of the pedestal.( tan 40° = 0.8391,\( \sqrt { 3 } \) = 1.732)

If tanθ+sinθ=P; tanθ-sinθ=q P.T P²-q²=4\(\sqrt{pq}\)

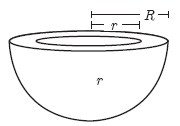
The internal and external radii of a hollow hemispherical shell are 3 m and 5 m respectively. Find the T.S.A. and C.S.A. of the shell.

The outer and the inner surface areas of a spherical copper shell are 576\(\pi\) cm² and 324\(\pi\) cm² respectively. Find the volume of the material required to make the shell.

A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter is 14 cm and the height of the vessel is 13 cm. Find the capacity of the vessel.

The measurements of the diameters (in cms) of the plates prepared in a factory are given below. Find its standard deviation.

Diameter(cm)	21-24	25-28	29-32	3-6	37-40	41-44
Number of plates	15	18	20	16	8	7

In a class of 35, students are numbered from 1 to 35. The ratio of boys to girls is 4 : 3. The roll numbers of students begin with boys and end with girls. Find the probability that a student selected is either a boy with prime roll number or a girl with composite roll number or an even roll number.

The standard deviation of some temperature data in degree celsius (⁰C) is 5. If the data were converted into degree Fahrenheit (⁰F) then what is the variance?

Find the co-efficient of variation for the following data: 16, 13, 17,21, 18.