- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Physics
-

Chemistry
-

Maths
-

Accountancy
-

Introductory Micro and Macroeconomics
-

Business Studies
-

Economics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Tamil
-

Bio Technology
-

Engineering Graphics
-

Entrepreneurship
-

Hindi Core
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Political Science
-

Psychology
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Mathematics
-

Chemistry
-

Biology
-

Physics
-

Business Studies
-

Accountancy
-

Economics
-

Computer Science
-

Bio Technology
-

English
-

Enterprenership
-

Geography
-

Hindi
-

History
-

Home Science
-

Physical Education
-

Political Science
-

Psychology
-

Sociology
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Mathematics
-

Social Science
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Science
-

Social Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students
Full Portion Two Marks Question Paper
10th Standard
-
Reg.No. :
Maths
Time :
01:00:00 Hrs
Total Marks :
50
-
If A x B = {(3,2), (3, 4), (5,2), (5, 4)} then find A and B.
-
The arrow diagram shows a relationship between the sets P and Q. Write the relation in
(i) Set builder form
(ii) Roster form
(iii) What is the domain and range of R.
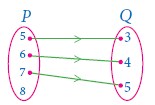
-
A plane is flying at a speed of 500 km per hour. Express the distanced travelled by the plane as function of time t in hours.
-
If f(x) = 3x - 2, g(x) = 2x + k and if f o g = f o f, then find the value of k..
-
State whether the graph represent a function. Use vertical line test.
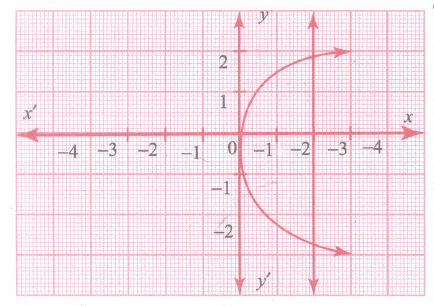
-
Let A = {0, 1, 2, 3} and B = {1, 3, 5, 7, 9} be two sets. Let f : A \(\rightarrow\)B be a function given by f(x) = 2x + 1. Represent this function as an arrow .
-
Find the square root of \(1+\frac { 1 }{ { x }^{ 6 } } +\frac { 2 }{ { x }^{ 3 } } \)
-
Determine the nature of the roots for the following quadratic equations
\(\sqrt { 2 } { t }^{ 2 }-3t+3\sqrt { 2 } \) = 0 -
In the matrix A = \(\left[ \begin{matrix} 8 \\ -1 \\ \begin{matrix} 1 \\ 6 \end{matrix} \end{matrix}\begin{matrix} 9 \\ \sqrt { 7 } \\ \begin{matrix} 4 \\ 8 \end{matrix} \end{matrix}\begin{matrix} 4 \\ \frac { \sqrt { 3 } }{ 2 } \\ \begin{matrix} 3 \\ -11 \end{matrix} \end{matrix}\begin{matrix} 3 \\ 5 \\ \begin{matrix} 0 \\ 1 \end{matrix} \end{matrix} \right] \), write The order of the matrix
-
Using quadratic formula solve the following equations.
p2x2 + (P2 -q2) X - q2 = 0 -
In the Figure, AD is the bisector of \(\angle\)BAC, if A = 10 cm, AC = 14 cm and BC = 6 cm. Find BD and DC.
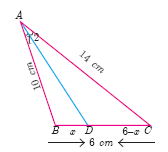
-
\(\triangle\) LMN is a right angled triangle with \(\angle\)L = 90o. A circle is inscribed in it. The lengths of the sides containing the right angle are 6 cm and 8 cm. Find the radius of the circle.
-
In fig. if PQ || BC and PR || CD prove that
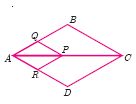
\(\frac { QB }{ AQ } =\frac { DR }{ AR } \) -
In figure if PQ || RS Prove that \(\Delta POQ\sim \Delta SOQ\)
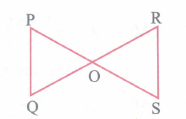
-
In figure the line segment XY is parallel to side AC of \(\Delta ABC\) and it divides the triangle into two parts of equal areas. Find the ratio \(\cfrac { AX }{ AB } \)
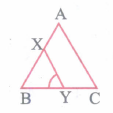
-
If the three points (3, - 1) , (a, 3) and (1, - 3) are collinear, find the value of a.
-
Find the equation of a straight line parallel to Y axis and passing through the point of intersection of the lines 4x + 5y = 13 and x - 8y + 9 = 0
-
Find the equation of a line through the given pair of points (2, 3) and (-7, -1)
-
prove the following identity.
\(\sqrt { \frac { 1+sin\theta }{ 1-sin\theta } } =sec\theta +tan\theta\) -
calculate \(\angle \)BAC in the given triangles ( tan 69.4° = 2.6604 )
-
A metallic sphere of radius 16 cm is melted and recast into small spheres each of radius 2 cm. How many small spheres can be obtained?
-
If the radii of the circular ends of a conical bucket which is 45 cm high are 28 cm and 7 cm, find the capacity of the bucket. (Use π = \(\frac{22}{7}\))
-
Find the range and coefficient of range of the following data.
43.5, 13.6, 18.9, 38.4, 61.4, 29.8 -
The marks scored by 5 students in a test for 50 marks are 20, 25, 30, 35, 40. Find the S.D for the marks. If the marks are converted for 100 marks, find the S.D. for newly obtained marks.
25 x 2 = 50






 10th Standard Maths Syllabus
10th Standard Maths Syllabus  10th Standard Maths Study Materials
10th Standard Maths Study Materials

Reviews & Comments about 10th Maths - Full Portion Two Marks Question Paper
Write your Comment