If n(A x B) = 6 and A = {1,3} then n(B) is

The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is

If \(\triangle\)ABC is an isosceles triangle with \(\angle\)C = 90^o and AC = 5 cm, then AB is

If in \(\triangle\)ABC, DE || BC, AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm then the length of AE is

The slope of the line which is perpendicular to a line joining the points (0, 0) and (– 8, 8) is

A straight line has equation 8y = 4x + 21. Which of the following is true

(1 + tan \(\theta \) + sec\(\theta \)) (1 + cot\(\theta \) - cosec\(\theta \)) is equal to 

If sin A = \(\frac{1}{2}\), then the value of cot A is ___________

If ∆ABC is right angled at C, then the value of cos (A + B) is ___________

The value of sin² θ + \(\frac { 1 }{ 1+{ tan }^{ 2 }\theta } \) of ___________

The sum of all deviations of the data from its mean is

If a letter is chosen at random from the English alphabets {a, b,...,z}, then the probability that the letter chosen precedes x

IF the probability of the non-happening of a event is q, then the probability of happening of that event is 

The variance of 5 values is 16. If each value is doubled them the standard deviation of new values is_______ 

If A x B = {(3,2), (3, 4), (5,2), (5, 4)} then find A and B.

Find x if gff(x) = fgg(x), given f(x) = 3x + 1 and g(x) = x + 3.

Let A =  {1,2, 3, 4} and B = {-1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} Let R = {(1, 3), (2, 6), (3, 10), (4, 9)} \(\subseteq \) A x B bea relation. Show that R is a function and find its domain, co-domain and the range of R.

Solve 8x \(\equiv \) 1 (mod 11)

If A = \(\left[ \begin{matrix} 1 & 2 & 1 \\ 2 & -1 & 1 \end{matrix} \right] \) and B = \(\left[ \begin{matrix} 2 & -1 \\ -1 & 4 \\ 0 & 2 \end{matrix} \right] \) show that (AB)^T = B^TA^T

Find the equation of a straight line passing through (5, - 3) and (7, - 4).

\(1+\frac { { cot }^{ 2 }\alpha }{ 1+cosex\alpha } =cosec\alpha\)

The range of a set of data is 13.67 and the largest value is 70.08. Find the smallest value.

Find the mean and variance of the first n natural numbers.

The marks scored by 5 students in a test for 50 marks are 20, 25, 30, 35, 40. Find the S.D for the marks. If the marks are converted for 100 marks, find the S.D. for newly obtained marks.

The arrow diagram shows a relationship between the sets P and Q. Write the relation in
(i) Set builder form
(ii) Roster form
(iii) What is the domain and range of R.

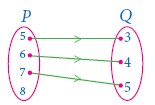
A functionf: [-7,6) \(\rightarrow\) R is defined as follows.

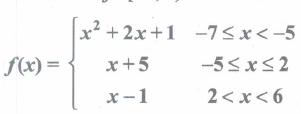
f(-7) - f(-3)

The 13^th term of an A.P is 3 and the sum of the first 13 terms is 234.Find the common difference and the sum of first 21 terms.

Which of the following list of numbers form an AP? If they form an AP, write the next two terms:
4,10,16, 22, ...

Draw the graph of y = x² - 4x + 3 and use it to solve x² - 6x + 9 = 0

Construct a triangle \(\triangle\)PQR such that QR = 5 cm, \(\angle\)P = 30^o and the altitude from P to QR is of length 4.2 cm.

The line joining the points A(0,5) and B(4,1) is a tangent to a circle whose centre C is at the point (4, 4) find The coordinates of the point of contact of tangent line AB with the circle

Find the area of a triangle vertices are(1, -1), (-4, 6) and (-3, -5).

If ATB=90^o then prove that
\(\sqrt { \frac { tanA\quad tanB+tanA\quad cotB }{ sinA\quad secB } } -\frac { { Sin }^{ 2 }A }{ { Cos }^{ 2 }A } =tanA\)

Find the co-efficient of variation for the following data: 16, 13, 17,21, 18.

A graph representing the function f (x) is given in Fig it is clear that f (9) = 2.
(i) Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
(ii) For what value of x is f (x) = 1?
(iii) Describe the following (i) Domain (ii) Range.
(iv) What is the image of 6 under f ?

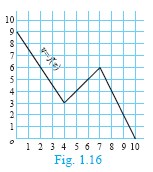
Using the functions f and g given below, find f o g and g o f. Check whether f o g = g o f.
f(x) = x - 6, g(x) = x²