If A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8} then state which of the following statement is true..

(a)

(A x C) ⊂ (B x D)

(b)

(B x D) ⊂ (A x C)

(c)

(A x B) ⊂ (A x D)

(d)

(D x A) ⊂ (B x A)

Let f(x) = \(\sqrt { 1+x^{ 2 } } \) then

(a)

f(xy) = f(x).f(y)

(b)

f(xy) ≥ f(x).f(y)

(c)

f(xy) ≤ f(x).f(y)

(d)

None of these

The sum of the exponents of the prime factors in the prime factorization of 1729 is

(a)

1

(b)

2

(c)

3

(d)

4

The next term of the sequence \(\frac { 3 }{ 16 } ,\frac { 1 }{ 8 } ,\frac { 1 }{ 12 } ,\frac { 1 }{ 18 } \), ..... is

(a)

\(\frac { 1 }{ 24 } \)

(b)

\(\frac { 1 }{ 27 } \)

(c)

\(\frac { 2 }{ 3 } \)

(d)

\(\frac { 1 }{ 81 } \)

\(\frac { x }{ { x }^{ 2 }-25 } -\frac { 8 }{ { x }^{ 2 }+6x+5 } \) gives

(a)

\(\frac { { x }^{ 2 }-7x+40 }{ \left( x-5 \right) \left( x+5 \right) } \)

(b)

\(\frac { { x }^{ 2 }+7x+40 }{ \left( x-5 \right) \left( x+5 \right) \left( x+1 \right) } \)

(c)

\(\frac { { x }^{ 2 }-7x+40 }{ \left( { x }^{ 2 }-25 \right) \left( x+1 \right) } \)

(d)

\(\frac { { x }^{ 2 }+10 }{ \left( { x }^{ 2 }-25 \right) \left( x+1 \right) } \)

If A = \(\left( \begin{matrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{matrix} \right) \), B = \(\left( \begin{matrix} 1 & 0 \\ 2 & -1 \\ 0 & 2 \end{matrix} \right) \) and C = \(\left( \begin{matrix} 0 & 1 \\ -2 & 5 \end{matrix} \right) \), Which of the following statements are correct?
(i) AB + C =  \(\left( \begin{matrix} 5 & 5 \\ 5 & 5 \end{matrix} \right) \)
(ii) BC = \(\left( \begin{matrix} 0 & 1 \\ 2 & -3 \\ -4 & 10 \end{matrix} \right) \)
(iii) BA + C = \(\left( \begin{matrix} 2 & 5 \\ 3 & 0 \end{matrix} \right) \)
(iv) (AB)C = \(\left( \begin{matrix} -8 & 20 \\ -8 & 13 \end{matrix} \right) \) 

(a)

(i) and (ii) only

(b)

(ii) and (iii) only

(c)

(iii) and (iv) only

(d)

all of these

In a given figure ST || QR, PS = 2 cm and SQ = 3 cm. Then the ratio of the area of \(\triangle\)PQR to the area \(\triangle\)PST is 

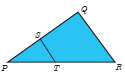(a)

25 : 4

(b)

25 : 7

(c)

25 : 11

(d)

25 : 13

The straight line given by the equation x = 11 is

(a)

parallel to X axis

(b)

parallel to Y axis

(c)

passing through the origin

(d)

passing through the point (0,11)

A straight line has equation 8y = 4x + 21. Which of the following is true

(a)

The slope is 0.5 and the y intercept is 2.6

(b)

The slope is 5 and the y intercept is 1.6

(c)

The slope is 0.5 and the y intercept is 1.6

(d)

The slope is 5 and the y intercept is 2.6

When proving that a quadrilateral is a trapezium, it is necessary to show

(a)

Two sides are parallel

(b)

Two parallel and two non-parallel sides

(c)

Opposite sides are parallel

(d)

All sides are of equal length

When proving that a quadrilateral is a parallelogram by using slopes you must find

(a)

The slopes of two sides

(b)

The slopes of two pair of opposite sides

(c)

The lengths of all sides

(d)

Both the lengths and slopes of two sides

(2, 1) is the point of intersection of two lines.

(a)

x - y - 3 = 0; 3x - y - 7 = 0

(b)

x + y = 3; 3x + y = 7

(c)

3x + y = 3; x + y = 7

(d)

x + 3y - 3 = 0; x - y - 7 = 0

If sin \(\theta \) = cos \(\theta \), then 2 tan² \(\theta \) + sin² \(\theta \) -1 is equal to 

(a)

\(\frac { -3 }{ 2 } \)

(b)

\(\frac { 3 }{ 2 } \)

(c)

\(\frac { 2 }{ 3 } \)

(d)

\(\frac { -2 }{ 3 } \)

(1 + tan \(\theta \) + sec\(\theta \)) (1 + cot\(\theta \) - cosec\(\theta \)) is equal to 

(a)

0

(b)

1

(c)

2

(d)

-1

a cot \(\theta \) + b cosec\(\theta \) = p and b cot \(\theta \) + a cosec\(\theta \) = q then p²- q² is equal to 

(a)

a² - b²

(b)

b² - a²

(c)

a² + b²

(d)

b - a

The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is

(a)

20, 10\(\sqrt { 3 } \)

(b)

30, 5\(\sqrt { 3 } \)

(c)

20, 10

(d)

30, 10\(\sqrt { 3 } \)

Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is

(a)

\(\sqrt { 2 } \) x

(b)

\(\frac { x }{ 2\sqrt { 2 } } \)

(c)

\(\frac { x }{ \sqrt { 2 } } \)

(d)

2x

The total surface area of a cylinder whose radius is \(\frac{1}{3}\)of its height is

(a)

\(\frac { 9\pi { h }^{ 2 } }{ 8 } \) sq.units

(b)

24\(\pi\)h² sq.units

(c)

\(\frac { 8\pi { h }^{ 2 } }{ 9 } \) sq.units

(d)

\(\frac { 56\pi { h }^{ 2 } }{ 9 } \) sq.units

If the radius of the base of a cone is tripled and the height is doubled then the volume is

(a)

made 6 times

(b)

made 18 times

(c)

made 12 times

(d)

unchanged

A solid sphere of radius x cm is melted and cast into a shape of a solid cone of same radius. The height of the cone is

(a)

3x cm

(b)

x cm

(c)

4x cm

(d)

2x cm

A shuttle cock used for playing badminton has the shape of the combination of

(a)

a cylinder and a sphere

(b)

a hemisphere and a cone

(c)

a sphere and a cone

(d)

frustum of a cone and a hemisphere

The volume (in cm³) of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is

(a)

\(\frac{4}{3}\pi\)

(b)

\(\frac{10}{3}\pi\)

(c)

\(5\pi\)

(d)

\(\frac{20}{3}\pi\)

The sum of all deviations of the data from its mean is

(a)

Always positive

(b)

always negative

(c)

zero

(d)

non-zero integer

Variance of first 20 natural numbers is

(a)

32.25

(b)

44.25

(c)

33.25

(d)

30

Kamalam went to play a lucky draw contest. 135 tickets of the lucky draw were sold. If the probability of Kamalam winning is \(\frac{1}{9}\), then the number of tickets bought by Kamalam is

(a)

5

(b)

10

(c)

15

(d)

20