If A = {5,6}, B = {4,5,6}, C = {5,6,7}, Show that A x A = (B x B) ∩ (C x C)

Let A = {x \(\in \) W| x < 2}, B = {x \(\in \) N| 1 < x ≤ 4} and C = (3,5). Verify that
A x (B U C) = (A x B) U (A x C)

A graph representing the function f (x) is given in Fig it is clear that f (9) = 2.
(i) Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
(ii) For what value of x is f (x) = 1?
(iii) Describe the following (i) Domain (ii) Range.
(iv) What is the image of 6 under f ?

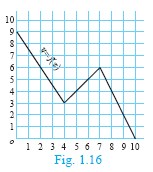
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal squares from the corners and turning up the sides as shown Fig. Express the volume V of the box as a function of x.

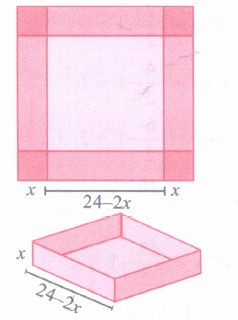
A function f: [-5,9] ⟶ R is defined as follows:
\(f(x)=\left[\begin{array}{ll} 6 x+1 & \text { if }-5 \leq x<2 \\ 5 x^{2}-1 & \text { if } 2 \leq x<6 \\ 3 x-4 & \text { if } 6 \leq x \leq 9 \end{array}\right.\)
Find
i) f(-3) + f(2)
ii) f(7) - f(1)
iii) 2f(4) + f(8)
iv)  \(\frac { 2f(-2)-f(6) }{ f(4)+f(-2) } \)

Find the HCF of 396, 504, 636.

Use Euclid’s Division Algorithm to find the Highest Common Factor (HCF) of 
340 and 412

Find the HCF of 252525 and 363636

Find the sum of 0.40 + 0.43 + 0.46 + ....+ 1

When the positive integers a, b and c are divided by 13 the respective remainders are 9, 7 and 10. Find the remainder When a + b + c is divided by 13.

A boat takes 1.6 hours longer to go 36 kms up a river than down the river. If the speed of the water current is 4 km per hr, what is the speed of the boat in still water?

At t minutes past 2 pm, the time needed to 3 pm is 3 minutes less than \(\frac {t^{2}}{4}\). Find t.

Vani, her father and her grand father have an average age of 53. One-half of her grand father’s age plus one-third of her father’s age plus one fourth of Vani’s age is 65. Four years ago if Vani’s grandfather was four times as old as Vani then how old are they all now?

Find the square root of 64x⁴ - 16x³ + 17x² - 2x + 1

A pole has to be erected at a point on the boundary of a circular ground of diameter 20 m in such a way that the difference of its distances from two diametrically opposite fixed gates P and Q on the boundary is 4 m. Is it possible to do so? If answer is yes at what distance from the two gates should the pole be erected?

If A = \(\left[ \begin{matrix} 3 & 1 \\ -1 & 2 \end{matrix} \right] \) show that A² - 5A + 7I₂ = 0

Find the square root of the following expressions
(6x² + x - 1)(3x² + 2x - 1)(2x² + 3x + 1)

A boy of height 90cm is walking away from the base of a lamp post at a speed of 1.2m/sec. If the lamppost is 3.6m above the ground, find the length of his shadow cast after 4 seconds.

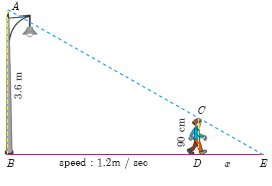
Construct a triangle \(\triangle\)PQR such that QR = 5 cm, \(\angle\)P = 30^o and the altitude from P to QR is of length 4.2 cm.

5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall

A circle is inscribed in \(\triangle\)ABC having sides 8 cm, 10 cm and 12 cm as shown in figure, find AD, BE and CF.

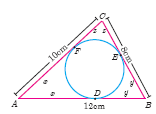
Show that the angle bisectors of a triangle are concurrent.

The graph relates temperatures y (in Fahrenheit degree) to temperatures x (in Celsius degree) Find the slope and y intercept

You are downloading a song. The percent y (in decimal form) of mega bytes remaining to get downloaded in x seconds is given by y = -0.1x + 1.
Graph the equation.

The probability that a person will get an electrification contract is \(\frac{3}{5}\) and the probability that he will not get plumbing contract is \(\frac{5}{8}\). The probability of getting atleast one contract is \(\frac{5}{7}\). What is the probability that he will get both?