- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Physics
-

Chemistry
-

Maths
-

Accountancy
-

Introductory Micro and Macroeconomics
-

Business Studies
-

Economics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Tamil
-

Bio Technology
-

Engineering Graphics
-

Entrepreneurship
-

Hindi Core
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Political Science
-

Psychology
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Mathematics
-

Chemistry
-

Biology
-

Physics
-

Business Studies
-

Accountancy
-

Economics
-

Computer Science
-

Bio Technology
-

English
-

Enterprenership
-

Geography
-

Hindi
-

History
-

Home Science
-

Physical Education
-

Political Science
-

Psychology
-

Sociology
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Mathematics
-

Social Science
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Science
-

Social Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students

10th Standard English Medium Maths Subject Book Back 5 Mark Questions with Solution Part - I Jun-12 , 2021
QB365 provides detailed and simple solution for every book back questions in class 10 Maths subject.It will helps to get more idea about question pattern in every book back questions with solution.
10th Standard English Medium Maths Subject Book Back 5 Mark Questions with Solution Part - I
10th Standard
-
Reg.No. :
Maths
Time :
01:00:00 Hrs
Total Marks :
50
-
If A = {5,6}, B = {4,5,6}, C = {5,6,7}, Show that A x A = (B x B) ∩ (C x C)
-
Let A = {x \(\in \) W| x < 2}, B = {x \(\in \) N| 1 < x ≤ 4} and C = (3,5). Verify that
A x (B U C) = (A x B) U (A x C) -
A graph representing the function f (x) is given in Fig it is clear that f (9) = 2.
(i) Find the following values of the function
(a) f(0)
(b) f(7)
(c) f(2)
(d) f(10)
(ii) For what value of x is f (x) = 1?
(iii) Describe the following (i) Domain (ii) Range.
(iv) What is the image of 6 under f ?
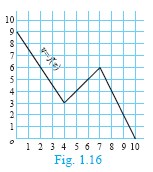
-
An open box is to be made from a square piece of material, 24 cm on a side, by cutting equal squares from the corners and turning up the sides as shown Fig. Express the volume V of the box as a function of x.
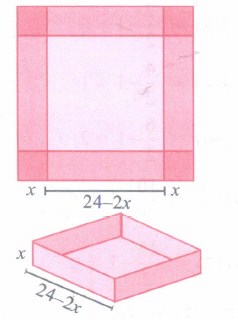
-
A function f: [-5,9] ⟶ R is defined as follows:
\(f(x)=\left[\begin{array}{ll} 6 x+1 & \text { if }-5 \leq x<2 \\ 5 x^{2}-1 & \text { if } 2 \leq x<6 \\ 3 x-4 & \text { if } 6 \leq x \leq 9 \end{array}\right.\)
Find
i) f(-3) + f(2)
ii) f(7) - f(1)
iii) 2f(4) + f(8)
iv) \(\frac { 2f(-2)-f(6) }{ f(4)+f(-2) } \) -
Find the HCF of 396, 504, 636.
-
Use Euclid’s Division Algorithm to find the Highest Common Factor (HCF) of
340 and 412 -
Find the HCF of 252525 and 363636
-
Find the sum of 0.40 + 0.43 + 0.46 + ....+ 1
-
When the positive integers a, b and c are divided by 13 the respective remainders are 9, 7 and 10. Find the remainder When a + b + c is divided by 13.
-
A boat takes 1.6 hours longer to go 36 kms up a river than down the river. If the speed of the water current is 4 km per hr, what is the speed of the boat in still water?
-
At t minutes past 2 pm, the time needed to 3 pm is 3 minutes less than \(\frac {t^{2}}{4}\). Find t.
-
Vani, her father and her grand father have an average age of 53. One-half of her grand father’s age plus one-third of her father’s age plus one fourth of Vani’s age is 65. Four years ago if Vani’s grandfather was four times as old as Vani then how old are they all now?
-
Find the square root of 64x4 - 16x3 + 17x2 - 2x + 1
-
A pole has to be erected at a point on the boundary of a circular ground of diameter 20 m in such a way that the difference of its distances from two diametrically opposite fixed gates P and Q on the boundary is 4 m. Is it possible to do so? If answer is yes at what distance from the two gates should the pole be erected?
-
If A = \(\left[ \begin{matrix} 3 & 1 \\ -1 & 2 \end{matrix} \right] \) show that A2 - 5A + 7I2 = 0
-
Find the square root of the following expressions
(6x2 + x - 1)(3x2 + 2x - 1)(2x2 + 3x + 1) -
A boy of height 90cm is walking away from the base of a lamp post at a speed of 1.2m/sec. If the lamppost is 3.6m above the ground, find the length of his shadow cast after 4 seconds.
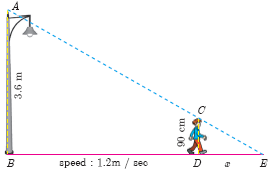
-
Construct a triangle \(\triangle\)PQR such that QR = 5 cm, \(\angle\)P = 30o and the altitude from P to QR is of length 4.2 cm.
-
5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall
-
A circle is inscribed in \(\triangle\)ABC having sides 8 cm, 10 cm and 12 cm as shown in figure, find AD, BE and CF.
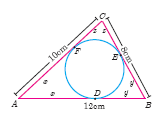
-
Show that the angle bisectors of a triangle are concurrent.
-
The graph relates temperatures y (in Fahrenheit degree) to temperatures x (in Celsius degree) Find the slope and y intercept
-
You are downloading a song. The percent y (in decimal form) of mega bytes remaining to get downloaded in x seconds is given by y = -0.1x + 1.
Graph the equation. -
The probability that a person will get an electrification contract is \(\frac{3}{5}\) and the probability that he will not get plumbing contract is \(\frac{5}{8}\). The probability of getting atleast one contract is \(\frac{5}{7}\). What is the probability that he will get both?
5 Marks
25 x 5 = 125






 10th Standard Maths Syllabus
10th Standard Maths Syllabus  10th Standard Maths Study Materials
10th Standard Maths Study Materials

Reviews & Comments about 10th Standard English Medium Maths Subject Book Back 5 Mark Questions with Solution Part - I
Write your Comment