Show that \(\triangle\) PST~\(\triangle\) PQR 

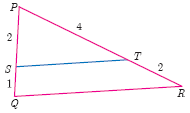
Check whether the which triangles are similar and find the value of x.
(i)

(ii)

A vertical stick of length 6 m casts a shadow 400 cm long on the ground and at the same time a tower casts a shadow 28 m long. Using similarity, find the height of the tower.

In the adjacent figure, \(\triangle\)ABC is right angled at C and DE\(\bot \) AB. Prove that \(\triangle\)ABC~\(\triangle\)ADE and hence find the lengths of AE and DE.

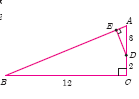
In the Figure, AD is the bisector of \(\angle\)BAC, if A = 10 cm, AC = 14 cm and BC = 6 cm. Find BD and DC.

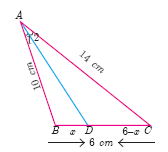
Check whether AD is bisector \(\angle\)A of \(\triangle\)ABC in each of the following AB = 5cm, AC = 10cm, BD = 1.5cm and CD = 3.5cm

In the rectangle WXYZ, XY+YZ = 17 cm, and XZ + YW = 26 cm .Calculate the length and breadth of the rectangle

If radii of two concentric circles are 4 cm and 5 cm then find the length of the chord of one circle which is a tangent to the other circle

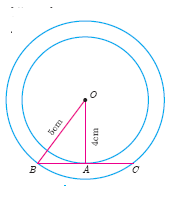
In the figure, if BD\(\bot \)AC and CE \(\bot \) AB, prove that
(i) \(\Delta AEC\sim \Delta ADB\)
(ii)  \(\frac { CA }{ AB } =\frac { CE }{ DB } \) 

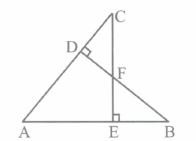
D is the mid point of side BC and AE \(\bot \) BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that
\({ b }^{ 2 }={ p }^{ 2 }+ax+\frac { { a }^{ 2 } }{ 4 } \)