- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Physics
-

Chemistry
-

Maths
-

Accountancy
-

Introductory Micro and Macroeconomics
-

Business Studies
-

Economics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Tamil
-

Bio Technology
-

Engineering Graphics
-

Entrepreneurship
-

Hindi Core
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Political Science
-

Psychology
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Mathematics
-

Chemistry
-

Biology
-

Physics
-

Business Studies
-

Accountancy
-

Economics
-

Computer Science
-

Bio Technology
-

English
-

Enterprenership
-

Geography
-

Hindi
-

History
-

Home Science
-

Physical Education
-

Political Science
-

Psychology
-

Sociology
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Mathematics
-

Social Science
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Science
-

Social Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students

10th Standard Mathematics All Chapter Creative Questions-I-2020 Feb-07 , 2020
10th Standard Mathematics All Chapter Creative Questions-I-2020
Creative Questions Part-III
10th Standard
-
Reg.No. :
Maths
Time :
01:30:00 Hrs
Total Marks :
100
-
If \(f(x)=\frac { x+1 }{ x-2 } ,g(x)=\frac { 1+2x }{ x-1 } \) then fog(x) is ___________
(a)Constant function
(b)Quadratic function
(c)Cubic function
(d)Identify function
-
Sum of infinite terms of G.P is 12 and the first term is 8. What is the fourth term of the G.P?
(a)\(\frac { 8 }{ 27 } \)
(b)\(\frac { 4 }{ 27 } \)
(c)\(\frac { 8 }{ 20 } \)
(d)\(\frac { 1 }{ 3 } \)
-
Choose the correct answer
(i) Every scalar matrix is an identity matrix
(ii) Every identity matrix is a scalar matrix
(iii) Every diagonal matrix is an identity matrix
(iv) Every null matrix is a scalar matrix(a)(i) and (iii) only
(b)(iii) only
(c)(iv) only
(d)(ii) and (iv) only
-
Two concentric circles if radii a and b where a>b are given. The length of the chord of the circle which touches the smaller circle is ____________
(a)\(\sqrt { { a }^{ 2 }-{ b }^{ 2 } } \)
(b)\(\sqrt { { a }^{ 2 }-{ b }^{ 2 } } \)
(c)\(\sqrt { { a }^{ 2 }+{ b }^{ 2 } } \)
(d)\(2\sqrt { { a }^{ 2 }+{ b }^{ 2 } } \)
-
Three circles are drawn with the vertices of a triangle as centres such that each circle touches the other two if the sides of the triangle are 2cm,3cm and 4 cm. find the diameter of the smallest circle.
(a)1 cm
(b)3 cm
(c)5 cm
(d)4 cm
-
Find the value of P, given that the line \(\frac { y }{ 2 } =x-p\) passes through the point (-4, 4) is ____________
(a)-4
(b)-6
(c)0
(d)8
-
If sec θ + tan θ = n, and sec θ - tan θ = 0, then the value of mn is ___________
(a)2
(b)1
(c)土1
(d)土2
-
The ratio of the volumes of two spheres is 8 : 27. If r and R are the radii of sphere respectively, Then (R - r) : r is ___________
(a)1:2
(b)1:3
(c)2:3
(d)4:9
-
The radius of a wire is decreased to one-third of the original. If volume the same, then the length will be increased _______of the original.
(a)3 times
(b)6 times
(c)9 times
(d)27 times
-
When three coins are tossed, the probability of getting the same face on all the three coins is ___________
(a)\(\frac { 1 }{ 8 } \)
(b)\(\frac { 1 }{ 4 } \)
(c)\(\frac { 3 }{ 8 } \)
(d)\(\frac { 1 }{ 3 } \)
-
Let A = {0, 1, 2, 3} and B = {1, 3, 5, 7, 9} be two sets. Let f: A \(\rightarrow\)B be a function given by f(x) = 2x + 1. Represent this function as a graph.
-
Use Euclid's algorithm to find the HCF of 4052 and 12756.
-
Prove that the equation x2(a2+b2)+2x(ac+bd)+(c2+ d2) = 0 has no real root if ad≠bc.
-
In figure the line segment XY is parallel to side AC of \(\Delta ABC\) and it divides the triangle into two parts of equal areas. Find the ratio \(\cfrac { AX }{ AB } \)
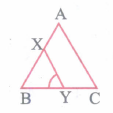
-
If A (-5, 7), B (-4, -5), C (-1, -6) and D (4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.
-
Find the depth of a cylindrical tank of radius 28 m, if its capacity is equal to that of a rectangular tank of size 28 m x 16 m x 11 m.
-
The marks scored by 5 students in a test for 50 marks are 20, 25, 30, 35, 40. Find the S.D for the marks. If the marks are converted for 100 marks, find the S.D. for newly obtained marks.
-
Let f = {(2, 7); (3, 4), (7, 9), (-1, 6), (0, 2), (5,3)} be a function from A = {-1,0, 2, 3, 5, 7} to B = {2, 3, 4, 6, 7, 9}. Is this
(i) an one-one function
(ii) an onto function,
(iii) both one and onto function? -
Which of the following list of numbers form an AP? If they form an AP, write the next two terms:
1,-1,-3, -5, ... -
A chess board contains 64 equal squares and the area of each square is 6.25 cm2, A border round the board is 2 cm wide.
-
BL and CM are medians of a triangle ABC right angled at A.
Prove that 4(BL2 + CM2) = 5BC2. -
Find the coordinates at the points of trisection (i.e. points dividing in three equal parts) of the line segment joining the points A(2, -2) and B(-7, 4).
-
Evaluate \(\frac { tan{ 65 }^{ o } }{ tan{ 25 }^{ o } } \)
-
Find the number of coins, 1.5 cm is diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
-
Find the co-efficient of variation for the following data: 16, 13, 17,21, 18.
-
The following table represents a function from A = {5, 6, 8, 10} to B = {19, 15, 9, 11}, where f(x) = 2x - 1. Find the values of a and b.
x 5 6 8 10 f(x) a 11 b 19 -
Find the sum of first 24 terms of the list of numbers whose nth term is given by an = 3 + 2n.
-
Find two consecutive natural numbers whose product is 20.
-
The perpendicular from A on side BC at a \(\triangle\)ABC intersects BC at D such that DB = 3 CD. Prove that 2AB2 = 2AC2 + BC2.
-
Find the value of k if the points A(2, 3), B(4, k) and (6, -3) are collinear.
-
From a point on a bridge across a river, the angles of depression of the banks on opposite sides at the river are 30° and 45°, respectively. If the bridge is at a height at 3 m from the banks, find the width at the river.
-
A spherical ball of iron has been melted and made into small balls. If the radius of each smaller ball is one-fourth of the radius of the original one, how many such balls can be made?
-
S.D. of a data is 2102, mean is 36.6, then find its C.V.
Part-A
10 x 1 = 10
Part-B
8 x 2 = 16
Part-C
8 x 5 = 40
Part-D
8 x 8 = 64






 10th Standard Maths Syllabus
10th Standard Maths Syllabus  10th Standard Maths Study Materials
10th Standard Maths Study Materials

Reviews & Comments about 10th Standard Mathematics All Chapter Creative Questions-I-2020
Write your Comment