If function f : N⟶N, f(x) = 2x then the function is, then the function is ___________

The difference between the remainders when 6002 and 601 are divided by 6 is ____________

The parabola y = -3x² is ___________

If triangle PQR is similar to triangle LMN such that 4PQ = LM and QR = 6 cm then MN is equal to ____________

If ABC is a triangle and AD bisects A, AB = 4cm, BD = 6cm, DC = 8cm then the value of AC is ____________

Find the slope and the y-intercept of the line \(3y-\sqrt { 3x } +1=0\) is ____________

If tan θ = cot θ the value of sec θ is ___________

It S₁ denotes the total surface area of a sphere of radius r and S₂ denotes the total surface area of a cylinder of base radius r and height 2r, then ___________

A cone of height 9 cm with diameter of its base 18 cm is carved out from a wooden solid sphere of radius 9 cm. The percentage of wood wasted is

A number x is chosen at random from -4, -3, -2, -1, 0, 1, 2, 3, 4. The probability that \(\left| x \right| \le 3\) is ___________

Let A = {0, 1, 2, 3} and B = {1, 3, 5, 7, 9} be two sets. Let f: A \(\rightarrow\)B be a function given by  f(x) = 2x + 1. Represent this function as  a table.

Find the LCM and HCF of 6 and 20 by the prime factorisation method.

Find the values of k for which the following equation has equal roots.
(k - 12)r + 2(k - 12)x + 2 = 0

In figure if PQ || RS Prove that \(\Delta POQ\sim \Delta SOQ\)

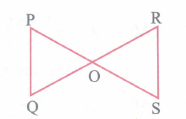
If A (-5, 7), B (-4, -5), C (-1, -6) and D (4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.

In a right triangle ABC, right-angled at B, if tan A = 1, then verify that 2 sin A cos A = 1.

If the radii of the circular ends of a conical bucket which is 45 cm high are 28 cm and 7 cm, find the capacity of the bucket. (Use π = \(\frac{22}{7}\))

Find the standard deviation of 30, 80, 60, 70, 20, 40, 50 using the direct method.

A function f: [-7,6) \(\rightarrow\) R is defined as follows.

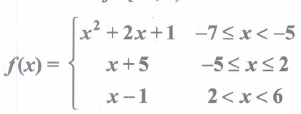
\(\cfrac { 4f(-3)+2f(4) }{ f(-6)-3f(1) } \)

In a flower bed, there are 23 rose plants in the first row, 21 in the second, 19 is the third, and so on. There are 5 rose plants in the last row. How many rows are there in the flower bed?

A chess board contains 64 equal squares and the area of each square is 6.25 cm², A border round the board is 2 cm wide.

BL and CM are medians of a triangle ABC right angled at A.
Prove that 4(BL² + CM²) = 5BC².

If the points A(6, 1), B(8, 2), C(9, 4) and D(P, 3) are the vertices of a parallelogram, taken in order. Find the value of P.

If sin (A - B) = \(\frac12\),  cos (A + B) = \(\frac12\), 0^o < A + ≤  90°, A > B, find A and B.

What is the ratio of the volume of a cylinder, a cone, and a sphere. If each has the same diameter and same height?

C.V. of a data is 69%, S.D. is 15.6, then find its mean.

The following table represents a function from A = {5, 6, 8, 10} to B = {19, 15, 9, 11}, where f(x) = 2x - 1. Find the values of a and b.

Find the sum of first 24 terms of the list of numbers whose nth term is given by a_n = 3 + 2n.

Find two consecutive natural numbers whose product is 20.

The perpendicular from A on side BC at a \(\triangle\)ABC intersects BC at D such that DB = 3 CD. Prove that 2AB² = 2AC² + BC².

Find the value of k if the points A(2, 3), B(4, k) and (6, -3) are collinear.

From a point on a bridge across a river, the angles of depression of the banks on opposite sides at the river are 30° and 45°, respectively. If the bridge is at a height at 3 m from the banks, find the width at the river.

A spherical ball of iron has been melted and made into small balls. If the radius of each smaller ball is one-fourth of the radius of the original one, how many such balls can be made?

Final the probability of choosing a spade or a heart card from a deck of cards.