- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Physics
-

Chemistry
-

Maths
-

Accountancy
-

Introductory Micro and Macroeconomics
-

Business Studies
-

Economics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Tamil
-

Bio Technology
-

Engineering Graphics
-

Entrepreneurship
-

Hindi Core
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Political Science
-

Psychology
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Mathematics
-

Chemistry
-

Biology
-

Physics
-

Business Studies
-

Accountancy
-

Economics
-

Computer Science
-

Bio Technology
-

English
-

Enterprenership
-

Geography
-

Hindi
-

History
-

Home Science
-

Physical Education
-

Political Science
-

Psychology
-

Sociology
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Mathematics
-

Social Science
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Science
-

Social Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students

10th Standard Mathematics Book Back and Important Questions-I-2019-2020 Feb-06 , 2020
10th Standard Mathematics Book Back and Important Questions-I-2019-2020
Important Questions Part-V
10th Standard
-
Reg.No. :
Maths
Part - A
Time :
01:00:00 Hrs
Total Marks :
60
-
If {(a, 8 ),(6, b)}represents an identity function, then the value of a and b are respectively
(a)(8,6)
(b)(8,8)
(c)(6,8)
(d)(6,6)
-
Let A = {1, 2, 3, 4} and B = {4, 8, 9, 10}. A function f: A ⟶ B given by f = {(1, 4), (2, 8), (3, 9), (4,10)} is a
(a)Many-one function
(b)Identity function
(c)One-to-one function
(d)Into function
-
If the order pairs (a, -1) and (5, b) belongs to {(x, y) | y = 2x + 3}, then a and b are __________
(a)-13, 2
(b)2, 13
(c)2, -13
(d)-2,13
-
If f(x) = ax - 2, g(x) = 2x - 1 and fog = gof, the value of a is ___________
(a)3
(b)-3
(c)\(\frac { 1 }{ 3 } \)
(d)13
-
If \(f(x)=\frac { 1 }{ x } \), and \(g(x)=\frac { 1 }{ { x }^{ 3 } } \) then f o g o(y), is ________
(a)\(\frac { 1 }{ { y }^{ 8 } } \)
(b)\(\frac { 1 }{ { y }^{ 6 } } \)
(c)\(\frac { 1 }{ { y }^{ 4 } } \)
(d)\(\frac { 1 }{ { y }^{ 3 } } \)
-
If f(x) + f(1 - x) = 2 then \(f\left( \frac { 1 }{ 2 } \right) \) is ___________
(a)5
(b)-1
(c)-9
(d)1
-
If 6 times of 6th term of an A.P. is equal to 7 times the 7th term, then the 13th term of the A.P. is
(a)0
(b)6
(c)7
(d)13
-
In an A.P., the first term is 1 and the common difference is 4. How many terms of the A.P. must be taken for their sum to be equal to 120?
(a)6
(b)7
(c)8
(d)9
-
If a and b are the two positive integers when a > b and b is a factor of a then HCF (a, b) is ____________
(a)b
(b)a
(c)ab
(d)\(\frac { a }{ b } \)
-
If pth, qth and rth terms of an A.P. are a, b, c respectively, then (a(q - r) + b(r - p) + c(p - q) is____________
(a)0
(b)a + b + c
(c)p + q + r
(d)pqr
-
The values of a and b if 4x4 - 24x3 + 76x2 + ax + b is a perfect square are
(a)100, 120
(b)10, 12
(c)-120, 100
(d)12, 10
-
Find the matrix X if 2X + \(\left( \begin{matrix} 1 & 3 \\ 5 & 7 \end{matrix} \right) =\left( \begin{matrix} 5 & 7 \\ 9 & 5 \end{matrix} \right) \)
(a)\(\left(\begin{array}{cc} -2 & -2 \\ 2 & -1 \end{array}\right)\)
(b)\(\left(\begin{array}{cc} 2 & 2 \\ 2 & -1 \end{array}\right)\)
(c)\(\left(\begin{array}{ll} 1 & 2 \\ 2 & 2 \end{array}\right)\)
(d)\(\left(\begin{array}{ll} 2 & 1 \\ 2 & 2 \end{array}\right)\)
-
If \(\frac { p }{ q } =a\) then \(\frac { { p }^{ 2 }+{ q }^{ 2 } }{ { p }^{ 2 }-{ q }^{ 2 } } \) ___________
(a)\(\frac { { a }^{ 2 }+1 }{ { a }^{ 2 }-1 } \)
(b)\(\frac { 1+{ a }^{ 2 } }{ 1-{ a }^{ 2 } } \)
(c)\(\frac { 1-{ a }^{ 2 } }{ 1-{ +a }^{ 2 } } \)
(d)\(\frac { { a }^{ 2 }-1 }{ { a }^{ 2 }+1 } \)
-
A Quadratic polynomial whose one zero is 5 and sum of the zeroes is 0 is given by ___________
(a)x2-25
(b)x2-5
(c)x2-5x
(d)x2-5x+5
-
If \(2A+3B=\left[ \begin{matrix} 2 & -1 & 4 \\ 3 & 2 & 5 \end{matrix} \right] \) and \(A+2B=\left[ \begin{matrix} 5 & 0 & 3 \\ 1 & 6 & 2 \end{matrix} \right] \) then B = [hint: B = (A+2B)-(2+3B)]
(a)\(\left[ \begin{matrix} 8 & -1 & -2 \\ -1 & 10 & -1 \end{matrix} \right] \)
(b)\(\left[ \begin{matrix} 8 & -1 & 2 \\ -1 & 10 & -1 \end{matrix} \right] \)
(c)\(\left[ \begin{matrix} 8 & 1 & 2 \\ -1 & 10 & -1 \end{matrix} \right] \)
(d)\(\left[ \begin{matrix} 8 & 1 & 2 \\ 1 & 10 & 1 \end{matrix} \right] \)
-
The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is
(a)\(6\frac { 2 }{ 3 } cm\)
(b)\(\frac { 10\sqrt { 6 } }{ 3 } cm\)
(c)\(66\frac { 2 }{ 3 } cm\)
(d)15 cm
-
The two tangents from an external points P to a circle with centre at O are PA and PB. If \(\angle APB\) = 70o then the value of \(\angle AOB\) is
(a)100°
(b)110°
(c)120°
(d)130°
-
If triangle PQR is similar to triangle LMN such that 4PQ = LM and QR = 6 cm then MN is equal to ____________
(a)12 cm
(b)24 cm
(c)10 cm
(d)36 cm
-
The ratio of the areas of two similar triangles is equal to ____________
(a)The ratio of their corresponding sides
(b)The cube of the ratio of their corresponding sides
(c)The ratio of their corresponding attitudes
(d)The square of the ratio of their corresponding sides
-
If ABC is a triangle and AD bisects A, AB = 4cm, BD = 6cm, DC = 8cm then the value of AC is ____________
(a)\(\frac { 16 }{ 3 } cm\)
(b)\(\frac { 32 }{ 3 } cm\)
(c)\(\frac { 3 }{ 16 } cm\)
(d)\(\frac { 1 }{ 2 } cm\)
-
When proving that a quadrilateral is a parallelogram by using slopes you must find
(a)The slopes of two sides
(b)The slopes of two pair of opposite sides
(c)The lengths of all sides
(d)Both the lengths and slopes of two sides
-
(2, 1) is the point of intersection of two lines.
(a)x - y - 3 = 0; 3x - y - 7 = 0
(b)x + y = 3; 3x + y = 7
(c)3x + y = 3; x + y = 7
(d)x + 3y - 3 = 0; x - y - 7 = 0
-
Find the equation of the line passing the point which is parallel to the y axis (5, 3) is ____________
(a)y = 5
(b)y = 3
(c)x = 5
(d)x = 3
-
In a right angle triangle, right angled at B, if the side BC is parallel to x axis, then the slope of AB is ___________
(a)\(\sqrt { 3 } \)
(b)\(\frac { 1 }{ \sqrt { 3 } } \)
(c)1
(d)not defined
-
If the ratio of the height of a tower and the length of its shadow is \(\sqrt{3}: 1\), then the angle of elevation of the sun has measure
(a)45°
(b)30°
(c)90°
(d)60°
-
The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to
(a)\(\sqrt { 3 } \) b
(b)\(\frac { b }{ 3 } \)
(c)\(\frac { b }{ 2 } \)
(d)\(\frac { b }{ \sqrt { 3 } } \)
-
If a sin (90 - θ) of (90o - θ) = cos(90o - θ)tan equal to ___________
(a)0
(b)1
(c)-1
(d)2
-
(sec A + tan A)(1 - sin A) is equal to ___________
(a)sec A
(b)sin A
(c)cosec A
(d)cos A
-
The top of two poles of height 18.5m and 7m are connected by a wire. If the wire makes an angle of measures 360o with horizontal, then the length of the wire is ____________
(a)23m
(b)18m
(c)28m
(d)25.5m
-
In a hollow cylinder, the sum of the external and internal radii is 14 cm and the width is 4 cm. If its height is 20 cm, the volume of the material in it is
(a)5600\(\pi\) cm3
(b)1120\(\pi\) cm3
(c)56\(\pi\) cm3
(d)3600\(\pi\) cm3
-
The height and radius of the cone of which the frustum is a part are h1 units and r1 units respectively. Height of the frustum is h2 units and radius of the smaller base is r2 units. If h2 : h1 = 1:2 then r2 : r1 is
(a)1:3
(b)1:2
(c)2:1
(d)3:1
-
The radius of base of a cone 5 cm and height is 12 cm. The slant height of the cone ___________
(a)13 cm
(b)17 cm
(c)7 cm
(d)60 cm
-
The volume of a frustum if a cone of height L and ends-radio and r1 and r2 is ___________
(a)\(\frac{1}{3}\)πh1(r12+r22+r1r2)
(b)\(\frac{1}{3}\)πh(r12+r22-r1r2)
(c)πh(r12+r22+r1r2)
(d)πh(r12+r22-r1r2)
-
A cylinder having radius 1 m and height 5 m is completely filled with milk. In how many conical flasks can this milk be filled if the radius and height is 50 cm each?
(a)50
(b)500
(c)120
(d)160
-
If a letter is chosen at random from the English alphabets {a, b....,z}, then the probability that the letter chosen precedes x ____________
(a)\(\frac { 12 }{ 13 } \)
(b)\(\frac { 1 }{ 13 } \)
(c)\(\frac { 23 }{ 26 } \)
(d)\(\frac { 3 }{ 26 } \)
-
Variance of first 20 natural numbers is
(a)32.25
(b)44.25
(c)33.25
(d)30
-
A page is selected at random from a book. The probability that the digit at units place of the page number chosen is less than 7 is
(a)\(\frac{3}{10}\)
(b)\(\frac{7}{10}\)
(c)\(\frac{3}{9}\)
(d)\(\frac{7}{9}\)
-
If the co-efficient of variation and standard deviation of a data are 35% and 7.7 respectively then the mean is ___________
(a)20
(b)30
(c)25
(d)22
-
If an event occurs surely, then its probability is _________.
(a)1
(b)0
(c)\(\frac { 1 }{ 2 } \)
(d)\(\frac { 3 }{ 4 } \)
-
If the probability of non-happening of an event is, then probability of happening of the event is ___________
(a)1-q
(b)q
(c)\(\frac { q }{ 2 } \)
(d)2q
-
If f(x) = x2 - 1, g(x) = x - 2 find a, if g o f(a) = 1
-
Write the domain of the following real functions
p(x) = \(\frac { -5 }{ 4x^{ 2 }+1 }\) -
Let A = {1,2, 3, 4} and B = {-1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} Let R = {(1, 3), (2, 6), (3, 10), (4, 9)} \(\subseteq \) A x B be a relation. Show that R is a function and find its domain, co-domain and the range of R.
-
Let A = {0, 1, 2, 3} and B = {1, 3, 5, 7, 9} be two sets. Let f: A \(\rightarrow\)B be a function given by f(x) = 2x + 1. Represent this function as a table.
-
Let A = {0, 1, 2, 3} and B = {1, 3, 5, 7, 9} be two sets. Let f: A \(\rightarrow\)B be a function given by f(x) = 2x + 1. Represent this function as a graph.
-
Find the least positive value of x such that
5x \(\equiv \) 4 (mod 6) -
Find the number of terms in the following G.P. \(\frac { 1 }{ 3 } ,\frac { 1 }{ 9 } ,\frac { 1 }{ 27 } \),...\(\frac { 1 }{ 2187 } \)
-
Simplify
\(\frac { 4x }{ { x }^{ 2 }-1 } -\frac { x+1 }{ x-1 } \) -
If α and β are the roots of x2 + 7x + 10 = 0 find the values of
\(\frac { \alpha }{ \beta } +\frac { \beta }{ \alpha } \) -
In the rectangle WXYZ, XY+YZ = 17 cm, and XZ + YW = 26 cm .Calculate the length and breadth of the rectangle

-
If figure OPRQ is a square and \(\angle\)MLN=90o. Prove that
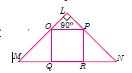
\(\triangle\)LOP~\(\triangle\)RPN -
Show that the given points are collinear: (-3, -4) , (7, 2) and (12, 5)
-
Find the equation of a straight line whose Slope is 5 and y intercept is -9
-
Find the equation of a line which passes through (5, 7) and makes intercepts on the axes equal in magnitude but opposite in sign.
-
A road is flanked on either side by continuous rows of houses of height \( 4\sqrt { 3 } \)m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road.
-
The horizontal distance between two buildings is 140 m. The angle of depression of the top of the first building when seen from the top of the second building is 30° . If the height of the first building is 60 m, find the height of the second building.(\(\sqrt { 3 } \) = 1.732)
-
4 persons live in a conical tent whose slant height is 19 cm. If each person require 22 cm2 of the floor area, then find the height of the tent.
-
A conical flask is full of water. The flask has base radius r units and height h units, the water poured into a cylindrical flask of base radius xr units. Find the height of water in the cylindrical flask.
-
Find the range and coefficient of range of the following data: 25, 67, 48, 53, 18, 39, 44.
-
Two coins are tossed together. What is the probability of getting different faces on the coins?
-
Let f = {(2, 7); (3, 4), (7, 9), (-1, 6), (0, 2), (5,3)} be a function from A = {-1,0, 2, 3, 5, 7} to B = {2, 3, 4, 6, 7, 9}. Is this
(i) an one-one function
(ii) an onto function,
(iii) both one and onto function? -
f(x) = (1+ x)
g(x) = (2x - 1)
Show that fo(g(x)) = gof(x) -
If the sum of the first 14 terms of an AP is 1050 and its first term is 10, find the 20th term.
-
Find the square root of the expression \(\frac { { x }^{ 2 } }{ { y }^{ 2 } } -\frac { 10x }{ y } +27-\frac { 10y }{ x } +\frac { { y }^{ 2 } }{ { x }^{ 2 } } \)
-
A ball rolls down a slope and travels a distance d = t2 - 0.75t feet in t seconds. Find the time when the distance travelled by the ball is 11.25 feet.
-
If A = \(\left[ \begin{matrix} 1 & -1 & 2 \end{matrix} \right] \), B = \(\left[ \begin{matrix} 1 & -1 \\ 2 & 1 \\ 1 & 3 \end{matrix} \right] \) and C = \(\left[ \begin{matrix} 1 & 2 \\ 2 & -1 \end{matrix} \right] \) show that (AB)C = A(BC)
-
The sum of two numbers is 15. If the sum of their reciprocals is \(\frac{3}{10}\), find the numbers.
-
P and Q are the mid-points of the sides CA and CB respectively of a \(\triangle\)ABC, right angled at C. Prove that 4(AQ2 + BP2) = 5AB2
-
Show that the angle bisectors of a triangle are concurrent.
-
If the points A(2, 2), B(–2, –3), C(1, –3) and D(x, y) form a parallelogram then find the value of x and y.
-
Two ships are sailing in the sea on either sides of a lighthouse as observed from the ships are \(30°\) and \(45°\) respectively. if the lighthouse is 200 m high, find the distance between the two ships. \(\left( \sqrt { 3 } =1.732 \right) \)
-
A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24°and the angle of depression of base of the statue is 34°. Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
-
Prove that \(\frac { ta{ n }^{ 2 }\theta -1 }{ ta{ n }^{ 2 }\theta +1 } \) = 1 - 2cos2\(\theta \)
-
If ATB=90o then prove that
\(\sqrt { \frac { tanA\quad tanB+tanA\quad cotB }{ sinA\quad secB } } -\frac { { Sin }^{ 2 }A }{ { Cos }^{ 2 }A } =tanA\) -
If the circumference of a conical wooden piece is 484 cm then find its volume when its height is 105 cm.
-
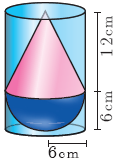
A solid consisting of a right circular cone of height 12 cm and radius 6 cm standing on a hemisphere of radius 6 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of the water displaced out of the cylinder, if the radius of the cylinder is 6 cm and height is 18 cm.
-
A shuttle cock used for playing badminton has the shape of a frustum of a cone is mounted on a hemisphere. The diameters of the frustum are 5 cm and 2 cm. The height of the entire shuttle cock is 7 cm. Find its external surface area.
-
The temperature of two cities A and B in a winter season are given below.
Temperature of city A (in degree Celsius) 18 20 22 24 26 Temperature of city B (in degree Celsius) 11 14 15 17 18 Find which city is more consistent in temperature changes?
-
Two dice are rolled together. Find the probability of getting a doublet or sum of faces as 4.
-
From a well-shuffled pack of 52 cards, a card is drawn at random. Find the probability of it being either a red king or a black queen.
-
Let A = {1, 2} and B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}, Verify whether A x C is a subset of B x D?
-
How many terms of the AP: 24, 21, 18, ... must be taken so that their sum is 78?
-
Find two consecutive natural numbers whose product is 20.
-
Construct a triangle \(\triangle\)PQR such that QR = 5 cm, \(\angle\)P = 30o and the altitude from P to QR is of length 4.2 cm.
-
Draw \(\angle\)PQR such that PQ = 6.8 cm, vertical angle is 50° and the bisector of the vertical angle meets the base at D where PD = 5.2 cm.
-
Find the equation of a line whose intercepts on the x and y axes are given below. -5, \(\frac 34\)
-
Find a relation between x and y if the points (x, y) (1, 2) and (7, 0) are collinear.
-
Express cot 85° + cos 75° in terms of trigonometric ratios of angles between 0° and 45°.
-
A wooden article was made by scooping out a hemisphere from each end of a cylinder as shown in figure. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm find the total surface area of the article.
-
Team A 50 20 10 30 30 Team B 40 60 20 20 10 Which team is more consistent?
Part - A
40 x 1 = 40
Part - B
20 x 2 = 40
Part - C
20 x 5 = 100
Part - D
10 x 8 = 80






 10th Standard Maths Syllabus
10th Standard Maths Syllabus  10th Standard Maths Study Materials
10th Standard Maths Study Materials

Reviews & Comments about 10th Standard Mathematics Book Back and Important Questions-I-2019-2020
Write your Comment