Let f be a function f : N ⟶ N be defined by f(x) = 3x + 2, x \(\in \) N
(i) Find the images of 1, 2, 3
(ii) Find the pre-images of 29, 53
(iii) Identify the type of function

A function f: [-5,9] ⟶ R is defined as follows:
\(f(x)=\left[\begin{array}{ll} 6 x+1 & \text { if }-5 \leq x<2 \\ 5 x^{2}-1 & \text { if } 2 \leq x<6 \\ 3 x-4 & \text { if } 6 \leq x \leq 9 \end{array}\right.\)
Find
i) f(-3) + f(2)
ii) f(7) - f(1)
iii) 2f(4) + f(8)
iv)  \(\frac { 2f(-2)-f(6) }{ f(4)+f(-2) } \)

A function f: (1,6) \(\rightarrow\)R is defined as follows:

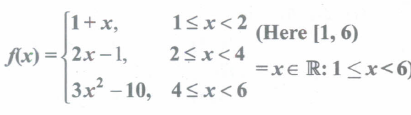
Find the value of f(5),

If R = {(a, -2), (-5, b), (8, c), (d, -1)} represents the identity function, find the values of a, b, c and 

Find the sum to n terms of the series
3 + 33 + 333 + ...to n terms

Find the sum of
5² + 10² + 15² +...+ 105²

Which of the following list of numbers form an AP? If they form an AP, write the next two terms:
-2, 2, -2, 2, -2

Determine the AP whose 3rd term is 5 and the 7^th term is 9.

Find the values of ‘k’, for which the quadratic equation kx² - (8k + 4)x + 81 = 0 has real and equal roots?

The roots of the equation x² + 6x - 4 = 0 are α, β. Find the quadratic equation whose roots are
α² and β²

The sum of two numbers is 15. If the sum of their reciprocals is \(\frac{3}{10}\), find the numbers.

A two digit number is such that the product of its digits is 12. When 36 is added to the number the digits interchange their places. Find the number.

If \(\triangle\)ABC~\(\triangle\)DEF such that area of \(\triangle\)ABC is 9cm² and the area of \(\triangle\)DEF is 16cm² and BC = 2.1 cm. Find the length of EF

A circle is inscribed in \(\triangle\)ABC having sides 8 cm, 10 cm and 12 cm as shown in figure, find AD, BE and CF.

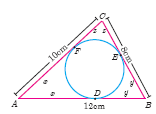
In \(AD\bot BC\) prove that AB² + CD² = BD² + AC². 

In figure 0 is any point inside a rectangle ABCD. Prove that OB² + OD² = OA² + OC²

If the points P(-1, -4), Q (b, c) and R(5, -1) are collinear and if 2b + c = 4, then find the values of b and c.

The floor of a hall is covered with identical tiles which are in the shapes of triangles. One such triangle has the vertices at (-3, 2), (-1, -1) and (1, 2). If the floor of the hall is completely covered by 110 tiles, find the area of the floor.

Find the coordinates at the points of trisection (i.e. points dividing in three equal parts) of the line segment joining the points A(2, -2) and B(-7, 4).

Find the value of k if the points A(2, 3), B(4, k) and (6, -3) are collinear.

prove that \(\frac { sinA }{ secA+tanA-1 } +\frac { cosA }{ cosecA+cotA-1 } =1\)

A kite is flying at a height of 75m above the ground, the string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is \(60°\).find the length of the string ,assuming that there is no slack in the string.

Express the ratios cos A, tan A and sec A in terms of sin A.

Evaluate \(\frac { tan{ 65 }^{ o } }{ tan{ 25 }^{ o } } \)

A right angled triangle PQR where ∠Q = 90^o is rotated about QR and PQ. If QR = 16 cm and PR = 20 cm, compare the curved surface areas of the right circular cones so formed by the triangle.

The internal and external diameter of a hollow hemispherical shell are 6 cm and 10 cm respectively. If it is melted and recast into a solid cylinder of diameter 14 cm, then find the height of the cylinder.

Find the number of coins, 1.5 cm is diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.

A wooden article was made by scooping out a hemisphere from each end of a cylinder as shown in figure. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm find the total surface area of the article.

The total marks scored by two students Sathya and Vidhya in 5 subjects are 460 and 480 with standard deviation 4.6 and 2.4 respectively. Who is more consistent in performance?

If two dice are rolled, then find the probability of getting the product of face value 6 or the difference of face values 5.

Team A	50	20	10	30	30
Team B	40	60	20	20	10

Which team is more consistent?

Final the probability of choosing a spade or a heart card from a deck of cards.