Let f(x) = \(\sqrt { 1+x^{ 2 } } \) then

(a)

f(xy) = f(x).f(y)

(b)

f(xy) ≥ f(x).f(y)

(c)

f(xy) ≤ f(x).f(y)

(d)

None of these

If g = {(1,1), (2,3), (3,5), (4,7)} is a function given by g(x) = αx + β then the values of α and β are

(a)

(-1,2)

(b)

(2,-1)

(c)

(-1,-2)

(d)

(1,2)

If f(x) = mx + n, when m and n are integers f(-2) = 7, and f(3) = 2 then m and n are equal to ___________

(a)

-1, -5

(b)

1, -9

(c)

-1, 5

(d)

1, 9

The next term of the sequence \(\frac { 3 }{ 16 } ,\frac { 1 }{ 8 } ,\frac { 1 }{ 12 } ,\frac { 1 }{ 18 } \), ..... is

(a)

\(\frac { 1 }{ 24 } \)

(b)

\(\frac { 1 }{ 27 } \)

(c)

\(\frac { 2 }{ 3 } \)

(d)

\(\frac { 1 }{ 81 } \)

If the sequence t₁, t₂, t₃... are in A.P. then the sequence t₆, t₁₂, t₁₈,.... is 

(a)

a Geometric Progression

(b)

an Arithmetic Progression

(c)

neither an Arithmetic Progression nor a Geometric Progression

(d)

a constant sequence

Given a₁ = -1, \(a=\frac { { a }_{ n } }{ n+2 } \), then a₄ is ____________

(a)

\(-\frac { 1 }{ 20 } \)

(b)

\(-\frac { 1 }{ 4 } \)

(c)

\(-\frac { 1 }{ 840 } \)

(d)

\(-\frac { 1 }{ 120 } \)

The number of points of intersection of the quadratic polynomial x² + 4x + 4 with the X axis is

(a)

0

(b)

1

(c)

0 or 1

(d)

2

For the given matrix A = \(\left( \begin{matrix} 1 \\ 2 \\ 9 \end{matrix}\begin{matrix} 3 \\ 4 \\ 11 \end{matrix}\begin{matrix} 5 \\ 6 \\ 13 \end{matrix}\begin{matrix} 7 \\ 8 \\ 15 \end{matrix} \right) \) the order of the matrix A^T is

(a)

2 x 3

(b)

3 x 2

(c)

3 x 4

(d)

4 x 3

\(\frac { { x }^{ 2 }+7x12 }{ { x }^{ 2 }+8x+15 } \times \frac { { x }^{ 2 }+5x }{ { x }^{ 2 }+6x+8 } =\_ \_ \_ \_ \_ \_ \_ \_ \_ \)

(a)

x+2

(b)

\(\frac { x }{ x+2 } \)

(c)

\(\frac { 35{ x }^{ 2 }+60x }{ { 48x }^{ 2 }+120 } \)

(d)

\(\frac { 1 }{ x+2 } \)

The two tangents from an external points P to a circle with centre at O are PA and PB. If \(\angle APB\) = 70^o then the value of \(\angle AOB\) is

(a)

100°

(b)

110°

(c)

120°

(d)

130°

In figure CP and CQ are tangents to a circle with centre at O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 7 cm, then the length of BR is

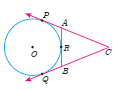(a)

6 cm

(b)

5 cm

(c)

8 cm

(d)

4 cm

In a triangle, the internal bisector of an angle bisects the opposite side. Find the nature of the triangle.

(a)

right angle

(b)

equilateral

(c)

scalene

(d)

isosceles

When proving that a quadrilateral is a trapezium, it is necessary to show

(a)

Two sides are parallel

(b)

Two parallel and two non-parallel sides

(c)

Opposite sides are parallel

(d)

All sides are of equal length

When proving that a quadrilateral is a parallelogram by using slopes you must find

(a)

The slopes of two sides

(b)

The slopes of two pair of opposite sides

(c)

The lengths of all sides

(d)

Both the lengths and slopes of two sides

Find the slope of the line 2y = x + 8 ____________

(a)

\(\frac { 1 }{ 2 } \)

(b)

1

(c)

8

(d)

2

Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is

(a)

\(\sqrt { 2 } \) x

(b)

\(\frac { x }{ 2\sqrt { 2 } } \)

(c)

\(\frac { x }{ \sqrt { 2 } } \)

(d)

2x

The angle of elevation of a cloud from a point h metres above a lake is \(\beta \). The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is

(a)

\(\frac { h\left( 1+tan\beta \right) }{ 1-tan\beta } \)

(b)

\(\frac { h\left( 1-tan\beta \right) }{ 1+tan\beta } \)

(c)

h tan(45°-\(\beta \))

(d)

none of these 

If cos9∝ = sin∝ and 9∝ < 90^o, then the value of tan t∝ is

(a)

\(\frac{1}{\sqrt{3}}\)

(b)

\({\sqrt{3}}\)

(c)

1

(d)

0

\(\frac { tan\theta }{ sec\theta } +\frac { tan\theta }{ sec\theta +1 } \) is equal to

(a)

2tanθ

(b)

2secθ

(c)

2cosecθ

(d)

2 tanθsecθ

The volume (in cm³) of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is

(a)

\(\frac{4}{3}\pi\)

(b)

\(\frac{10}{3}\pi\)

(c)

\(5\pi\)

(d)

\(\frac{20}{3}\pi\)

The height and radius of the cone of which the frustum is a part are h₁ units and r₁ units respectively. Height of the frustum is h₂ units and radius of the smaller base is r₂ units. If h₂ : h₁ = 1:2 then r₂ : r₁ is

(a)

1:3

(b)

1:2

(c)

2:1

(d)

3:1

It S₁ denotes the total surface area of a sphere of radius r and S₂ denotes the total surface area of a cylinder of base radius r and height 2r, then ___________

(a)

S₁ = S₂

(b)

S₁ > S₂

(c)

S₁ < S₂

(d)

S₁ = 2S₂

Kamalam went to play a lucky draw contest. 135 tickets of the lucky draw were sold. If the probability of Kamalam winning is \(\frac{1}{9}\), then the number of tickets bought by Kamalam is

(a)

5

(b)

10

(c)

15

(d)

20

If a letter is chosen at random from the English alphabets {a, b,...,z}, then the probability that the letter chosen precedes x

(a)

\(\frac{12}{13}\)

(b)

\(\frac{1}{13}\)

(c)

\(\frac{23}{26}\)

(d)

\(\frac{3}{26}\)

The mean of first first 10 odd natural number is ___________

(a)

5

(b)

10

(c)

20

(d)

19