Let A = {1, 2, 3, 4} and B = {4, 8, 9, 10}. A function f: A ⟶ B given by f = {(1, 4), (2, 8), (3, 9), (4,10)} is a

If f(x) = 2x² and g(x) = \(\frac{1}{3x}\), then f o g is

If f : R⟶R is defined by (x) = x² + 2, then the preimage 27 are _________

Let f(x) = x² - x, then f(x- 1) - (x + 1) is ___________

If function f : N⟶N, f(x) = 2x then the function is, then the function is ___________

If f is constant function of value \(\frac { 1 }{ 10 } \), the value of f(1) + f(2) + ... + f(100) is _________

The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is

If the sequence t₁, t₂, t₃... are in A.P. then the sequence t₆, t₁₂, t₁₈,.... is 

The difference between the remainders when 6002 and 601 are divided by 6 is ____________

A boy saves Rs. 1 on the first day Rs. 2 on the second day, Rs. 4 on the third day and so on. How much did the boy will save upto 20 days?

y² + \(\frac {1}{y^{2}}\) is not equal to

If the roots of the equation q²x² + p²x + r² = 0 are the squares of the roots of the equation qx² + px + r = 0, then q, p, r are in __________.

Which of the following is correct
(i) Every polynomial has finite number of multiples
(ii) LCM of two polynimials of degree 2 may be a constant
(iii) HCF of 2 polynomials may be constant
(iv) Degree of HCF of two polynomials is always less then degree of LCM

\(\frac { { x }^{ 2 }+7x12 }{ { x }^{ 2 }+8x+15 } \times \frac { { x }^{ 2 }+5x }{ { x }^{ 2 }+6x+8 } =\_ \_ \_ \_ \_ \_ \_ \_ \_ \)

If P and Q are matrices, then which of the following is true?

If \(\triangle\)ABC is an isosceles triangle with \(\angle\)C = 90^o and AC = 5 cm, then AB is

A tangent is perpendicular to the radius at the

If triangle PQR is similar to triangle LMN such that 4PQ = LM and QR = 6 cm then MN is equal to ____________

I the given figure DE||AC which of the following is true.

If the angle between two radio of a circle is ^o, the angle between the tangents at the end of the radii is ____________

If (5, 7), (3, p) and (6, 6) are collinear, then the value of p is

The point of intersection of 3x − y = 4 and x + y = 8 is

Find the ratio in which the line segment joining the points (-3, 10) and (6,-8) is internally divided by (-1, 6) ____________

If the mid-point of the line segment joining \(A\left( \frac { x }{ 2 } ,\frac { y+1 }{ 2 } \right) \) and B(x + 1, y-3) is C(5, -2) then find the values of x, y ____________

The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to

If (sin α + cosec α)² + (cos α + sec α)² = k + tan²α + cot²α, then the value of k is equal to

If sec θ + tan θ = n, and sec θ - tan θ = 0, then the value of mn is ___________

The value of sin² θ + \(\frac { 1 }{ 1+{ tan }^{ 2 }\theta } \) of ___________

The angle of elevation of the top of tree from a point at a distance of 250 m from its base is 60^o. The height of tree is ___________

The height of a right circular cone whose radius is 5 cm and slant height is 13 cm will be

The volume (in cm³) of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is

The material of a cone is converted into the shape of a cylinder of equal radius. If the height of the cylinder is 5 cm, then height of the cone is ___________

The curved surface area of a cylinder is 264 cm² and its volume is 924 cm². The ratio of diameter to its height is ___________

A floating boat having a length 3m and breadth 2m is floating on a lake. The boat sinks by 1 cm when a man gets into it. The mass of the man is (density of water is 10000 kg/m³)

A purse contains 10 notes of Rs. 2000, 15 notes of Rs. 500, and 25 notes of Rs. 200.One note is drawn at random. What is the probability that the note is either a Rs. 500, note or Rs. 200 note?

The range of the data 8, 8, 8, 8, 8. . . 8 is

The probability of getting a job for a person is \(\frac{x}{3}\). If the probability of not getting the job is \(\frac{2}{3}\)  then the value of x is

A number x is chosen at random from -4, -3, -2, -1, 0, 1, 2, 3, 4 find the probability that |x| ≤ 4

which of the following is true?

If the smallest value and co-efficient of range a data are 25 and 0.5 respectively. Then the largest value is ___________

Let A = {1,2,3} and B = {x| x is a prime number less than 10}. Find A x B and B x A.

Using the functions f and g given below, find f o g and g o f. Check whether f o g = g o f.
f(x) = x - 6, g(x) = x²

Let A =  {1,2, 3, 4} and B = {-1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} Let R = {(1, 3), (2, 6), (3, 10), (4, 9)} \(\subseteq \) A x B bea relation. Show that R is a function and find its domain, co-domain and the range of R.

Let A = {0, 1, 2, 3} and B = {1, 3, 5, 7, 9} be two sets. Let f: A \(\rightarrow\)B be a function given by  f(x) = 2x + 1. Represent this function as  a set of ordered pairs.

Let A = {0, 1, 2, 3} and B = {1, 3, 5, 7, 9} be two sets. Let f : A \(\rightarrow\)B be a function given by  f(x) = 2x + 1. Represent this function as an arrow .

Check whether the following sequences are in A.P. or not?
x + 2, 2x + 3, 3x + 4, ....

Find the first term and common difference of the Arithmetic Progressions whose n^th terms are given below t_n = -3 + 2n

Find the LCM of the following
8x⁴y², 48x²y⁴

Find the sum and product of the roots for each of the following quadratic equations:
2x² + 5x + 7 = 0

\(\angle A=\angle CED\) prove that \(\Delta\ CAB \sim \Delta CED\) Also find the value of x.

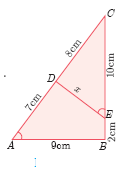
In fig. if PQ || BC and PR || CD prove that

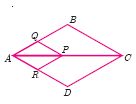
\(\frac { QB }{ AQ } =\frac { DR }{ AR } \)

Determine whether the sets of points are collinear? \((-\frac12 ,3)\), (- 5, 6) and (-8, 8)

Find the slope of the line which is Parallel to y = 0.7 x − 11

Find the slope of a line joining the points (sin θ, -cos θ) and (-sin θ, cos θ)

prove that \(\frac { sinA }{ 1+cosA } =\frac { 1-cosA }{ sinA } \) 

A tower stands vertically on the ground. from a point on the ground,which is 48m away from the foot of the tower, the angel of elevation of the top of  the tower is 30°.find the hieght of the tower.

The ratio of the volumes of two cones is 2 : 3. Find the ratio of their radii if the height of second cone is double the height of the first.

Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r units.

A die is rolled and a coin is tossed simultaneously. Find the probability that the die shows an odd number and the coin shows a head.

If A and B are two mutually exclusive events of a random experiment and P(not A) = 0.45, P(A U B) = 0.65, then find P(B).

Let f = {(2, 7); (3, 4), (7, 9), (-1, 6), (0, 2), (5,3)} be a function from A = {-1,0, 2, 3, 5, 7} to B = {2, 3, 4, 6, 7, 9}. Is this
(i) an one-one function
(ii) an onto function,
(iii) both oneone and onto function?

f(x) = (1+ x)
g(x) = (2x - 1)
Show that fo(g(x)) = gof(x)

If the sum of the first 14 terms of an AP is 1050 and its first term is 10, find the 20th term.

Iniya bought 50 kg of fruits consisting of apples and bananas. She paid twice as much per kg for the apple as she did for the banana. If Iniya bought Rs. 1800 worth of apples and Rs. 600 worth bananas, then how many kgs of each fruit did she buy?

Find X and Y if X + Y = \(\left[ \begin{matrix} 7 & 0 \\ 3 & 5 \end{matrix} \right] \) and X - Y = \(\left[ \begin{matrix} 3 & 0 \\ 0 & 4 \end{matrix} \right] \)

If A = \(\left[ \begin{matrix} 1 & 8 & 3 \\ 3 & 5 & 0 \\ 8 & 7 & 6 \end{matrix} \right] \), B = \(\left[ \begin{matrix} 8 & -6 & -4 \\ 2 & 11 & -3 \\ 0 & 1 & 5 \end{matrix} \right] \), C = \(\left[ \begin{matrix} 5 & 3 & 0 \\ -1 & -7 & 2 \\ 1 & 4 & 3 \end{matrix} \right] \) compute the following
\(\\ \frac { 1 }{ 2 } A-\frac { 3 }{ 2 } B\)

Seven years ago, Varun's age was five times the square of swati's age. Three years hence Swati's age will be two fifth of Varun's age. Find their present ages.

In \(\triangle\)ABC , with \(\angle\)B=90° , BC = 6 cm and AB = 8 cm, D is apoint on AC such that AD = 2 cm and E is the midpoint of AB. Join D to E and extend it to meet at F. Find BF.

An artist has created a triangular stained glass window and has one strip of small length left before completing the window. She needs to figure out the length of left out portion based on the lengths of the other sides as shown in the figure.

A(-3, 0) B(10, - 2) and C(12, 3) are the vertices of ΔABC. Find the equation of the altitude through A and B.

A kite is flying at a height of 75m above the ground,the string attached to the kite is temporarily tied to a point on the ground.The inclination of the string with the ground is \(60°\).find the length of the string ,assuming that there is no slack in the string.

A vertical pole fixed to the ground is divided in the ratio 1:9 by a mark on it with lower part shorter than the upper part. If the two parts subtend equal angles at a place on the ground, 25 m away from the base of the pole, what is the height of the pole?

if sin\(\theta \) (1 + sin²\(\theta \)) = cos²\(\theta \), then prove that cos⁶\(\theta \) - 4cos⁴\(\theta \) + 8cos²\(\theta \) = 4

The shadow of a tower, when the angle of elevation of the sum is 45^o is found to be 10 metres, longer than when it is 60^o. find the height of the tower

Find the volume of the iron used to make a hollow cylinder of height 9 cm and whose internal and external radii are 21 cm and 28 cm respectively

A hemispherical section is cut out from one face of a cubical block  such that the diameter l of the hemisphere is equal to side length of the cube. Determine the surface area of the remaining solid.

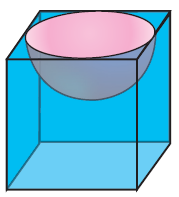
As shown in figure a cubical block of side 7 cm is surmounted by a hemisphere. Find the surface area of the solid.

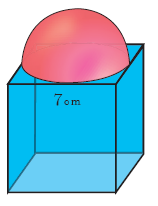
The mean and variance of seven observations are 8 and 16 respectively. If five of these are 2, 4, 10, 12 and 14, then find the remaining two observations.

If two dice are rolled, then find the probability of getting the product of face value 6 or the difference of face values 5.

The King, Queen and Jack of the suit spade are removed from a deck of 52 cards. One card is selected from the remaining cards. Find the probability of getting
(i) a diamond
(ii) a queen
(iii) a spade
(iv) a heart card bearing the number 5.

Let A = {1, 2} and B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8}, Verify whether A x C is a subset of B x D?

How many terms of the AP: 24, 21, 18, ... must be taken so that their sum is 78?

Find two consecutive natural numbers whose product is 20.

Construct a triangle \(\triangle\)PQR such that QR = 5 cm, \(\angle\)P = 30^o and the altitude from P to QR is of length 4.2 cm.

Construct a \(\triangle\)PQR such that QR = 6.5 cm,\(\angle\)P = 60^oand the altitude from P to QR is of length 4.5 cm.

Find the equation of a line whose intercepts on the x and y axes are given below. 4, -6

Find the area of the triangle formed by the points P(-1, 5, 3), Q(6, -2) and R(-3, 4).

From a point on a bridge across a river, the angles of depression of the banks on opposite sides at the river are 30° and 45°, respectively. If the bridge is at a height at 3 m from the banks, find the width at the river.

A wooden article was made by scooping out a hemisphere from each end of a cylinder as shown in figure. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm find the total surface area of the article.

S.D. of a data is 2102, mean is 36.6, then find its C.V.