A = {a,b,p}, B = {2,3}, C = {p,q,r,s} then n[(A U C) x B] is

(a)

8

(b)

20

(c)

12

(d)

16

If there are 1024 relations from a set A = {1, 2, 3, 4, 5} to a set B, then the number of elements in B is

(a)

3

(b)

2

(c)

4

(d)

8

The range of the relation R = {(x, x²) |x is a prime number less than 13} is

(a)

{2,3,5,7}

(b)

{2,3,5,7,11}

(c)

{4,9,25,49,121}

(d)

{1,4,9,25,49,121}

Let A = {1, 2, 3, 4} and B = {4, 8, 9, 10}. A function f: A ⟶ B given by f = {(1, 4), (2, 8), (3, 9), (4,10)} is a

(a)

Many-one function

(b)

Identity function

(c)

One-to-one function

(d)

Into function

If f(x) = 2x² and g(x) = \(\frac{1}{3x}\), then f o g is

(a)

\(\\ \frac { 3 }{ 2x^{ 2 } } \)

(b)

\(\\ \frac { 2 }{ 3x^{ 2 } } \)

(c)

\(\\ \frac { 2 }{ 9x^{ 2 } } \)

(d)

\(\\ \frac { 1 }{ 6x^{ 2 } } \)

Euclid’s division lemma states that for positive integers a and b, there exist unique integers q and r such that a = bq + r , where r must satisfy

(a)

1 < r < b

(b)

0 < r < b

(c)

0 \(\le\) r < b

(d)

0 < r \(\le\) b

Given F₁ = 1, F₂ = 3 and F_n = F_n-1 + F_n-2 then F₅ is

(a)

3

(b)

5

(c)

8

(d)

11

An A.P. consists of 31 terms. If its 16^th term is m, then the sum of all the terms of this A.P. is

(a)

16 m

(b)

62 m

(c)

31 m

(d)

\(\frac { 31 }{ 2 } \) m

If the sequence t₁, t₂, t₃... are in A.P. then the sequence t₆, t₁₂, t₁₈,.... is 

(a)

a Geometric Progression

(b)

an Arithmetic Progression

(c)

neither an Arithmetic Progression nor a Geometric Progression

(d)

a constant sequence

The value of (1³ + 2³ + 3³ +...+15³) - (1 + 2 + 3 +...+ 15)is 

(a)

14400

(b)

14200

(c)

14280

(d)

14520

The solution of (2x - 1)² = 9 is equal to

(a)

-1

(b)

2

(c)

-1, 2

(d)

None of these

If A is a 2 x 3 matrix and B is a 3 x 4 matrix, how many columns does AB have

(a)

3

(b)

4

(c)

2

(d)

5

If number of columns and rows are not equal in a matrix then it is said to be a

(a)

diagonal matrix

(b)

rectangular matrix

(c)

square matrix

(d)

identity matrix

Find the matrix X if 2X + \(\left( \begin{matrix} 1 & 3 \\ 5 & 7 \end{matrix} \right) =\left( \begin{matrix} 5 & 7 \\ 9 & 5 \end{matrix} \right) \)

(a)

\(\left(\begin{array}{cc} -2 & -2 \\ 2 & -1 \end{array}\right)\)

(b)

\(\left(\begin{array}{cc} 2 & 2 \\ 2 & -1 \end{array}\right)\)

(c)

\(\left(\begin{array}{ll} 1 & 2 \\ 2 & 2 \end{array}\right)\)

(d)

\(\left(\begin{array}{ll} 2 & 1 \\ 2 & 2 \end{array}\right)\)

If A = \(\left( \begin{matrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{matrix} \right) \), B = \(\left( \begin{matrix} 1 & 0 \\ 2 & -1 \\ 0 & 2 \end{matrix} \right) \) and C = \(\left( \begin{matrix} 0 & 1 \\ -2 & 5 \end{matrix} \right) \), Which of the following statements are correct?
(i) AB + C =  \(\left( \begin{matrix} 5 & 5 \\ 5 & 5 \end{matrix} \right) \)
(ii) BC = \(\left( \begin{matrix} 0 & 1 \\ 2 & -3 \\ -4 & 10 \end{matrix} \right) \)
(iii) BA + C = \(\left( \begin{matrix} 2 & 5 \\ 3 & 0 \end{matrix} \right) \)
(iv) (AB)C = \(\left( \begin{matrix} -8 & 20 \\ -8 & 13 \end{matrix} \right) \) 

(a)

(i) and (ii) only

(b)

(ii) and (iii) only

(c)

(iii) and (iv) only

(d)

all of these

If in triangles ABC and EDF,\(\cfrac { AB }{ DE } =\cfrac { BC }{ FD } \) then they will be similar, when

(a)

\(\angle B=\angle E\)

(b)

\(\angle A=\angle D\)

(c)

\(\angle B=\angle D\)

(d)

\(\angle A=\angle F\)

In a given figure ST || QR, PS = 2 cm and SQ = 3 cm. Then the ratio of the area of \(\triangle\)PQR to the area \(\triangle\)PST is 

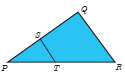(a)

25 : 4

(b)

25 : 7

(c)

25 : 11

(d)

25 : 13

If in \(\triangle\)ABC, DE || BC, AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm then the length of AE is

(a)

1.4 cm

(b)

1.8 cm

(c)

1.2 cm

(d)

1.05 cm

A tangent is perpendicular to the radius at the

(a)

centre

(b)

point of contact

(c)

infinity

(d)

chord

How many tangents can be drawn to the circle from an exterior point?

(a)

one

(b)

two

(c)

infinite

(d)

zero

A man walks near a wall, such that the distance between him and the wall is 10 units. Consider the wall to be the Y axis. The path travelled by the man is

(a)

x = 10

(b)

y = 10

(c)

x = 0

(d)

y = 0

The slope of the line joining (12, 3), (4, a) is \(\frac 18\). The value of ‘a’ is

(a)

1

(b)

4

(c)

-5

(d)

2

The slope of the line which is perpendicular to a line joining the points (0, 0) and (– 8, 8) is

(a)

–1

(b)

1

(c)

\(\frac13\)

(d)

-8

If A is a point on the Y axis whose ordinate is 8 and B is a point on the X axis whose abscissae is 5 then the equation of the line AB is

(a)

8x + 5y = 40

(b)

8x - 5y = 40

(c)

x = 8

(d)

y = 5

When proving that a quadrilateral is a parallelogram by using slopes you must find

(a)

The slopes of two sides

(b)

The slopes of two pair of opposite sides

(c)

The lengths of all sides

(d)

Both the lengths and slopes of two sides

The value of \(si{ n }^{ 2 }\theta +\frac { 1 }{ 1+ta{ n }^{ 2 }\theta } \) is equal to

(a)

 \(ta{ n }^{ 2 }\theta \)

(b)

1

(c)

\(cot^{ 2 }\theta \)

(d)

0

If sin \(\theta \) + cos\(\theta \) = a and sec \(\theta \) + cosec \(\theta \) = b, then the value of b(a² - 1) is equal to 

(a)

2a

(b)

3a

(c)

0

(d)

2ab

If the ratio of the height of a tower and the length of its shadow is \(\sqrt{3}: 1\), then the angle of elevation of the sun has measure

(a)

45°

(b)

30°

(c)

90°

(d)

60°

The electric pole subtends an angle of 30° at a point on the same level as its foot. At a second point ‘b’ metres above the first, the depression of the foot of the pole is 60°. The height of the pole (in metres) is equal to

(a)

\(\sqrt { 3 } \) b

(b)

\(\frac { b }{ 3 } \)

(c)

\(\frac { b }{ 2 } \)

(d)

\(\frac { b }{ \sqrt { 3 } } \)

The angle of elevation of a cloud from a point h metres above a lake is \(\beta \). The angle of depression of its reflection in the lake is 45°. The height of location of the cloud from the lake is

(a)

\(\frac { h\left( 1+tan\beta \right) }{ 1-tan\beta } \)

(b)

\(\frac { h\left( 1-tan\beta \right) }{ 1+tan\beta } \)

(c)

h tan(45°-\(\beta \))

(d)

none of these 

The height of a right circular cone whose radius is 5 cm and slant height is 13 cm will be

(a)

12 cm

(b)

10 cm

(c)

13 cm

(d)

5 cm

If the radius of the base of a right circular cylinder is halved keeping the same height, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is

(a)

1:2

(b)

1:4

(c)

1:6

(d)

1:8

The total surface area of a hemi-sphere is how much times the square of its radius.

(a)

\(\pi\)

(b)

4\(\pi\)

(c)

3\(\pi\)

(d)

2\(\pi\)

A frustum of a right circular cone is of height 16 cm with radii of its ends as 8 cm and 20 cm. Then, the volume of the frustum is

(a)

3328\(\pi\) cm³

(b)

3228\(\pi\) cm³

(c)

3240\(\pi\) cm³

(d)

3340\(\pi\) cm³

The volume (in cm³) of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is

(a)

\(\frac{4}{3}\pi\)

(b)

\(\frac{10}{3}\pi\)

(c)

\(5\pi\)

(d)

\(\frac{20}{3}\pi\)

Which of the following is not a measure of dispersion?

(a)

Range

(b)

Standard deviation

(c)

Arithmetic mean

(d)

Variance

The mean of 100 observations is 40 and their standard deviation is 3. The sum of squares of all observations is

(a)

40000

(b)

160900

(c)

160000

(d)

30000

Which of the following is incorrect?

(a)

P(A) > 1

(b)

0 ≤ P(A) ≤ 1

(c)

P(ф) = 0

(d)

P(A) + P(\(\bar { A } \)) = 1

Kamalam went to play a lucky draw contest. 135 tickets of the lucky draw were sold. If the probability of Kamalam winning is \(\frac{1}{9}\), then the number of tickets bought by Kamalam is

(a)

5

(b)

10

(c)

15

(d)

20

A purse contains 10 notes of Rs. 2000, 15 notes of Rs. 500, and 25 notes of Rs. 200. One note is drawn at random. What is the probability that the note is either a Rs. 500 note or Rs. 200 note?

(a)

\(\frac{1}{5}\)

(b)

\(\frac{3}{10}\)

(c)

\(\frac{2}{3}\)

(d)

\(\frac{4}{5}\)