Let A = {3,4,7,8} and B = {1,7,10}. Which of the following sets are relations from A to B?
R₁ = {(3,7), (4,7), (7,10), (8,1)}

Let f{(x, y)| x, y \(\in \) N and y = 2x}. be a relation on ℕ. Find the domain, co-domain and range. Is this relation a function?

Using horizontal line test (Fig.1.35(a), 1.35(b), 1.35(c)), determine which of the following functions are one – one.

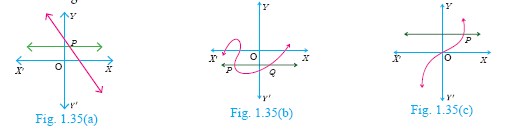
If f(x) = 3x - 2, g(x) = 2x + k and if f o g = f o f, then find the value of k..

Find the value of k, such that f o g = g o f
f(x) = 3x + 2, g(x) = 6x - k

Using the functions f and g given below, find f o g and g o f. Check wheather f o g = g o f
 f(x) = 3 + x, g(x) = x - 4

Find k, if f(k) = 2k - 1 and f o f(k) = 5.

Write the domain of the following real functions
p(x) = \(\frac { -5 }{ 4x^{ 2 }+1 }\)

Determine whether the graph given below represent functions. Give a reason for your answer concerning the graph.

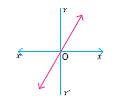
Let A = {1, 2, 3, 7} and B = {3, 0, –1, 7}, which of the following are relation from A to B ?
R₃ = {(2, –1), (7, 7), (1, 3)}

Can the number 6ⁿ, n being a natural number end with the digit 5 ? Give reason for your answer.

if m,n are natural numbers , for what values of m, does 2ⁿ x 5^m ends in 5?

Find the number of integer solutions of 3x \(\equiv \) 1 (mod 15).

First term a and common difference d are given below. Find the corresponding A.P
a = 5, d = 6

A man repays a loan of Rs. 65,000 by paying Rs. 400 in the first month and then increasing the payment by Rs. 300 every month. How long will it take for him to clear the loan?

Write the first three terms of the G.P. whose first term and the common ratio are given below
a = 6, r = 3

If a, b, c are in A.P. then show that 3^a, 3^b, 3^c are in G.P

Find the rational form of the number 0.6666....

Find the sum of
1 + 3 + 5 +..+ to 40 terms

Find the sum of
1² + 2² +...+ 19²

Find the least positive value of x such that
78 + x \(\equiv \) 3 (mod 5)

Find the general term for the following sequences.
\(\frac { 1 }{ 2 } ,\frac { 2 }{ 3 } ,\frac { 3 }{ 4 } \)

Find the first four terms of the sequences whose nth terms are given by
a_n = 2n² - 6

Which of the following sequences form a Geometric Progression?
\(\frac { 1 }{ 2 } \), 1, 2, 4,....

Find the LCM of the following
8x⁴y², 48x²y⁴

If α, β are the roots of the equation 2x² - x - 1 = 0, then form the equation whose roots are
\(\frac { 1 }{ \alpha } ,\frac { 1 }{ \beta } \)

Find the values of x, y and z from the following equations
\(\left[ \begin{matrix} 12 & 3 \\ x & \frac { 3 }{ 2 } \end{matrix} \right] =\left[ \begin{matrix} y & z \\ 3 & 5 \end{matrix} \right] \)

If A = \(\left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right] \), B = \(\left[ \begin{matrix} 1 & 7 & 0 \\ 1 & 3 & 1 \\ 2 & 4 & 0 \end{matrix} \right] \), find A + B.

Two examinations were conducted for three groups of students namely group 1, group 2, group 3 and their data on average of marks for the subjects Tamil, English, Science and Mathematics are given below in the form of matrices A and B. Find the total marks of both the examinations for all the three groups.

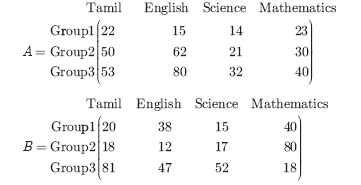
If A = \(\left[ \begin{matrix} 2 & 5 \\ 4 & 3 \end{matrix} \right] \), B = \(\left[ \begin{matrix} 1 & -3 \\ 2 & 5 \end{matrix} \right] \) find AB, BA and check if AB = BA?

Find the LCM and GCD for the following and verify that f(x) x g(x) = LCM x GCD
(x³ - 1)(x + 1), (x³ + 1)

Reduce the rational expressions to its lowest form
\(\frac { { x }^{ 2 }-16 }{ { x }^{ 2 }+8x+16 } \)

Multiply \(\frac { { x }^{ 4 }{ b }^{ 2 } }{ x-1 } \) by \(\frac { { x }^{ 2 }-1 }{ { a }^{ 4 }{ b }^{ 3 } } \)

Simplify
\(\frac { x+2 }{ x+3 } +\frac { x-1 }{ x-2 } \)

Determine the quadratic equations, whose sum and product of roots are
-(2 - a)², (a + 5)²

Find the sum and product of the roots for each of the following quadratic equations
x² + 3x = 0

Solve the following quadratic equations by formula method
\(\sqrt { 2 } { f }^{ 2 }-6f+3\sqrt { 2 } \) = 0

Determine the nature of the roots for the following quadratic equations
x² - x - 1 = 0

Determine the nature of the roots for the following quadratic equations
9a²b²x² - 24abcdx + 16c²d² = 0, a ≠ 0, b ≠ 0

\(\angle A=\angle CED\) prove that \(\Delta\ CAB \sim \Delta CED\) Also find the value of x.

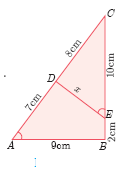
Two triangles QPR and QSR, right angled at P and S respectively are drawn on the same base QR and on the same side of QR. If PR and SQ intersect at T, prove that PT x TR = ST x TQ. \(\triangle\)

In the adjacent figure, \(\triangle\)ABCis right angled at C and DE\(\bot \) AB. Prove that \(\triangle\)ABC~\(\triangle\)ADE and hence find the lengths of AE and DE.

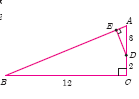
In the figure, if BD\(\bot \)AC and CE \(\bot \) AB, prove that
(i) \(\Delta AEC\sim \Delta ADB\)
(ii)  \(\frac { CA }{ AB } =\frac { CE }{ DB } \) 

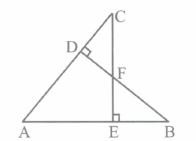
If figure OPRQ is a square and \(\angle\)MLN = 90^o. Prove that

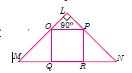
QR² = MQ x RN

In \(\triangle\)ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DE || BC AB = 5.6 cm, AD = 1.4 cm, AC = 7.2 cm and AE = 1.8 cm.

D is the mid point of side BC and AE \(\bot \) BC. If BC = a, AC = b, AB = c, ED = x, AD = p and AE = h, prove that
\({ b }^{ 2 }+{ c }^{ 2 }={ 2p }^{ 2 }+\frac { { a }^{ 2 } }{ 2 } \)

Find the area of the triangle whose vertices are (-3, 5) , (5, 6) and (5, - 2)

Vertices of given triangles are taken in order and their areas are provided aside. In each case, find the value of ‘p’?

S.No	Vertices	Area (sq.units)
(i)	(0, 0), (p, 8), (6, 2)	20
(ii)	(p, p), (5, 6), (5, -2)	32

In each of the following, Find the value of ‘a’ for which the given points are collinear. (2, 3), (4, a) and (6, –3)

What is the inclination of a line whose slope is 0

Show that the given vertices form a right angled triangle and check whether its satisfies Pythagoras theorem A(1, - 4) , B(2, - 3) and C(4, - 7)

Find the intercepts made by the line 4x − 9y + 36 = 0 on the coordinate axes.

Find the equation of a straight line passing through the point P(-5, 2) and parallel to the line joining the points Q(3, -2) and R(-5, 4).

Find the equation of a straight line whose Inclination is 45⁰ and y intercept is 11

Find the area of the triangle formed by the points :(–10, –4), (–8, –1) and (–3, –5)

Find the equation of a line through the given pair of points (2, 3) and (-7, -1)

prove that \(\frac { sec\theta }{ sin\theta } -\frac { sin\theta }{ cos\theta } =cot\theta \)

A tower stands vertically on the ground. from a point on the ground,which is 48m away from the foot of the tower, the angel of elevation of the top of  the tower is 30°.find the hieght of the tower.

Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height \(10\sqrt { 3 } m\)

From the top of a rock \(50\sqrt { 3 } \)m high, the angle of depression of a car on the ground is observed to be 30°. Find the distance of the car from the rock.

prove the following identitity tan⁴\(\theta \) + tan²\(\theta \) = sec⁴\(\theta \) - sec²\(\theta \) .

prove the following identity.
\(\frac { cos\theta }{ 1+sin\theta } \) = sec \(\theta \) - tan \(\theta \)

A garden roller whose length is 3 m long and whose diameter is 2.8 m is rolled to level a garden. How much area will it cover in 8 revolutions?

Find the diameter of a sphere whose surface area is 154 m².

The slant height of a frustum of a cone is 5 cm and the radii of its ends are 4 cm and 1 cm. Find its curved surface area.

A solid iron cylinder has total surface area of 1848 sq.m. Its curved surface area is five – sixth of its total surface area. Find the radius and height of the iron cylinder.

4 persons live in a conical tent whose slant height is 19 cm. If each person require 22 cm² of the floor area, then find the height of the tent.

A cone of height 24 cm is made up of modeling clay. A child reshapes it in the form of a cylinder of same radius as cone. Find the height of the cylinder.

Find the maximum volume of a cone that can be carved out of a solid hemisphere of radius r units.

Find the range and coefficient of range of the following data: 25, 67, 48, 53, 18, 39, 44.

Find the range and coefficient of range of the following data. 63, 89, 98, 125, 79, 108, 117, 68

Calculate the range of the following data..

Income	400-450	450-500	500-550	550-600	600-650
Number of workers	8	12	30	21	6

The following table gives the values of mean and variance of heights and weights of the 10th standard students of a school.

	Height	Weight
Mean	155 cm	46.50 kg
Variance	72.25 cm2	28.09 kg

Which is more varying than the other?

If n = 5 , \(\bar { x } \) = 6, Σx² = 765 then calculate the coefficient of variation.

What is the probability that a leap year selected at random will contain 53 saturdays. (Hint: 366 = 52 x 7 + 2)

Write the sample space for tossing three coins using tree diagram.

If P(A) = \(\frac{2}{3}\), P(B) = \(\frac{2}{5}\), P(A U B) = \(\frac{1}{3}\) then find P(A ∩ B).