If f: A ⟶ B is a bijective function and if n(B) = 7, then n(A) is equal to

Let f(x) = \(\sqrt { 1+x^{ 2 } } \) then

The value of (1³ + 2³ + 3³ +...+15³) - (1 + 2 + 3 +...+ 15)is 

Sum of first n terms of the series \(\sqrt { 2 } +\sqrt { 8 } +\sqrt { 18 } +...\) is ____________

The number of points of intersection of the quadratic polynomial x² + 4x + 4 with the X axis is

If \(\triangle\)ABC is an isosceles triangle with \(\angle\)C = 90^o and AC = 5 cm, then AB is

In a \(\triangle\)ABC, AD is the bisector \(\angle\)BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. The length of the side AC is

If A is a point on the Y axis whose ordinate is 8 and B is a point on the X axis whose abscissae is 5 then the equation of the line AB is

If sin \(\theta \) + cos\(\theta \) = a and sec \(\theta \) + cosec \(\theta \) = b, then the value of b(a² - 1) is equal to 

a cot \(\theta \) + b cosec\(\theta \) = p and b cot \(\theta \) + a cosec\(\theta \) = q then p²- q² is equal to 

The value of sin² θ + \(\frac { 1 }{ 1+{ tan }^{ 2 }\theta } \) of ___________

A shuttle cock used for playing badminton has the shape of the combination of

Variance of first 20 natural numbers is

The standard deviation is the ____ of variance 

Write the domain of the following real functions
 f(x) = \(\frac { 2x+1 }{ x-9 } \)

Find the n^th term of the following sequences,
2, 5, 10, 17,....,

Find the LCM and HCF of 6 and 20 by the prime factorisation method.

Find
\(\frac { { x }^{ 2 }-16 }{ x+1 } \div \frac { x-4 }{ x+4 } \)

Using quadratic formula solve the following equations.
p²x² + (P² -q²) X - q² = 0

In the Figure, AD is the bisector of \(\angle\)BAC, if A = 10 cm, AC = 14 cm and BC = 6 cm. Find BD and DC.

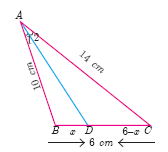
In figure if PQ || RS Prove that \(\Delta POQ\sim \Delta SOQ\)

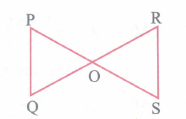
Find the equation of a line which passes through (5, 7) and makes intercepts on the axes equal in magnitude but opposite in sign.

Show that the points (1, 7), (4, 2), (-1,-1) and (-4,4) are the vertices of a square.

prove that \(\sqrt { \frac { 1+cos\theta }{ 1-cos\theta } } \) = cosec \(\theta \) + cot\(\theta \)

If the base area of a hemispherical solid is 1386 sq. metres, then find its total surface area?

Find the depth of a cylindrical tank of radius 28 m, if its capacity is equal to that of a rectangular tank of size 28 m x 16 m x 11 m.

The range of a set of data is 13.67 and the largest value is 70.08. Find the smallest value.

Find the standard deviation for the following data. 5, 10, 15, 20, 25. And also find the new S.D. if three is added to each value.

Let A, B, C ⊆ N and a function f : A ⟶ B be defined by f(x) = 2x + 1 and g : B ⟶ C be defined by g(x) = x². Find the range of f o g and g o f.

If R = {(a, -2), (-5, b), (8, c), (d, -1)} represents the identity function, find the values of a, b, c and 

Find the rational form of the number \(0.\bar { 123 } \)

In a flower bed, there are 23 rose plants in the first row, 21 in the second, 19 is the third, and so on. There are 5 rose plants in the last row. How many rows are there in the flower bed?

Simplify
\(\frac { 5{ t }^{ 2 } }{ 4t-8 } \times \frac { 6t-12 }{ 10t } \)

A ladder is placed against a wall such that its foot is at a distance of 2.5 m from the wall and its top reaches a window 6 m above the ground. Find the length of the ladder.

Find the equation of a straight line through the intersection of lines 5x − 6y = 2, 3x + 2y = 10 and perpendicular to the line 4x − 7y + 13 = 0

Find the value of k if the points A(2, 3), B(4, k) and (6, -3) are collinear.

An Aeroplane sets of from G on bearing of 24° towards H, a point 250 km away, at H it changes  course and heads towards J deviates further by 55° and a distance of 180 km away.
How far is J to the North of H?

\(\left( \begin{matrix} sin24°=0.4067\quad sin11°=0.1908 \\ cos24°=0.9135\quad cos11°=0.9816 \end{matrix} \right) \)

If sin 3A = cos (A - 26°), where 3A is an acute angle, find the value at A.

The internal and external diameter of a hollow hemispherical shell are 6 cm and 10 cm respectively. If it is melted and recast into a solid cylinder of diameter 14 cm, then find the height of the cylinder.

What is the ratio of the volume of a cylinder, a cone, and a sphere. If each has the same diameter and same height?

The King, Queen and Jack of the suit spade are removed from a deck of 52 cards. One card is selected from the remaining cards. Find the probability of getting
(i) a diamond
(ii) a queen
(iii) a spade
(iv) a heart card bearing the number 5.

C.V. of a data is 69%, S.D. is 15.6, then find its mean.