If the ordered pairs (a + 2, 4) and (5, 2a + b) are equal then (a, b) is

If f(x) = 2x² and g(x) = \(\frac{1}{3x}\), then f o g is

The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is

If p^th, q^th and r^th terms of an A.P. are a, b, c respectively, then (a(q - r) + b(r - p) + c(p - q) is____________

If (x - 6) is the HCF of x² - 2x - 24 and x² - kx - 6 then the value of k is

If \(\triangle\)ABC is an isosceles triangle with \(\angle\)C = 90^o and AC = 5 cm, then AB is

How many tangents can be drawn to the circle from an exterior point?

If slope of the line PQ is \(\frac { 1 }{ \sqrt { 3 } } \) then slope of the perpendicular bisector of PQ is

The value of \(si{ n }^{ 2 }\theta +\frac { 1 }{ 1+ta{ n }^{ 2 }\theta } \) is equal to

tan \(\theta \) cosec²\(\theta \) - tan\(\theta \) is equal to 

If x = r sin θ cos φ y = r sin θ. Then x² + y² + z²___________

A solid sphere of radius x cm is melted and cast into a shape of a solid cone of same radius. The height of the cone is

The range of the data 8, 8, 8, 8, 8. . . 8 is

The variance of 5 values is 16. If each value is doubled them the standard deviation of new values is_______ 

Using the functions f and g given below, find f o g and g o f. Check whether f o g = g o f
f(x) = 4x² - 1, g(x) = 1 + x

In an A.P. the sum of first n terms is \(\frac { { 5n }^{ 2 } }{ 2 } +\frac { 3n }{ 2 } \). Find the 17^th term

Find the LCM and HCF of 6 and 20 by the prime factorisation method.

Reduce the rational expressions to its lowest form
\(\frac { { x }^{ 2 }-16 }{ { x }^{ 2 }+8x+16 } \)

Prove that the equation x²(a²+b²)+2x(ac+bd)+(c²+ d²) = 0 has no real root if ad≠bc.

Show that \(\triangle\)PST~\(\triangle\)PQR 

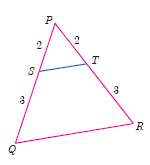
In figure the line segment XY is parallel to side AC of \(\Delta ABC\) and it divides the triangle into two parts of equal areas. Find the ratio \(\cfrac { AX }{ AB } \)

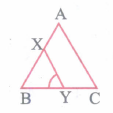
Find the intercepts made by the following lines on the coordinate axes. 4x + 3y + 12 = 0

Show that the points (1, 7), (4, 2), (-1,-1) and (-4,4) are the vertices of a square.

prove the following identity.
 \(\sqrt { \frac { 1+sin\theta }{ 1-sin\theta } } =sec\theta +tan\theta\)

The radius of a spherical balloon increases from 12 cm to 16 cm as air being pumped into it. Find the ratio of the surface area of the balloons in the two cases.

If the radii of the circular ends of a conical bucket which is 45 cm high are 28 cm and 7 cm, find the capacity of the bucket. (Use π = \(\frac{22}{7}\))

A die is rolled and a coin is tossed simultaneously. Find the probability that the die shows an odd number and the coin shows a head.

Find the standard deviation of 30, 80, 60, 70, 20, 40, 50 using the direct method.

Given that
\(f(x)=\left\{\begin{array}{cc} \sqrt{x-1} & x \geq 1 \\ 4 & x<1 \end{array}\right.\)
Find
i) f(0)
ii) f(3)
iii) f(a + 1) in terms of a (Given that a ≥ 0)

If R = {(a, -2), (-5, b), (8, c), (d, -1)} represents the identity function, find the values of a, b, c and 

If l^th, m^th and n^th terms of an A.P are x, y, z respectively, then show that  x(m - n) + y(n - l) + z(l - m) = 0

Which of the following list of numbers form an AP ? If they form an AP, write the next two terms:
1, 1, 1, 2, 2, 2, 3, 3,  3

If A = \(\left[ \begin{matrix} 1 & 1 \\ -1 & 3 \end{matrix} \right] \), B = \(\left[ \begin{matrix} 1 & 2 \\ -4 & 2 \end{matrix} \right] \), C = \(\left[ \begin{matrix} -7 & 6 \\ 3 & 2 \end{matrix} \right] \) verify that A(B + C) = AB + AC

In \(AD\bot BC\) prove that AB² + CD² = BD² + AC². 

A triangular shaped glass with vertices at A(-5, -4), B(1, 6) and C(7, -4) has to be painted. If one bucket of paint covers 6 square feet, how many buckets of paint will be required to paint the whole glass, if only one coat of paint is applied.

Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3, -2) and (2, 3).

A vertical pole fixed to the ground is divided in the ratio 1:9 by a mark on it with lower part shorter than the upper part. If the two parts subtend equal angles at a place on the ground, 25 m away from the base of the pole, what is the height of the pole?

If 15tan² θ+4 sec² θ=23 then find the value of (secθ+cosecθ)² -sin² θ

The volume of a solid hemisphere is 29106 cm³. Another hemisphere whose volume is two-third of the above is carved out. Find the radius of the new hemisphere.

Find the number of coins, 1.5 cm is diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.

A bag contains 6 green balls, some black and red balls. Number of black balls is as twice as the number of red balls. Probability of getting a green ball is thrice the probability of getting a red ball. Find (i) number of black balls (ii) total number of balls.

Final the probability of choosing a spade or a heart card from a deck of cards.