- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Physics
-

Chemistry
-

Maths
-

Accountancy
-

Introductory Micro and Macroeconomics
-

Business Studies
-

Economics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Tamil
-

Bio Technology
-

Engineering Graphics
-

Entrepreneurship
-

Hindi Core
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Political Science
-

Psychology
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Mathematics
-

Chemistry
-

Biology
-

Physics
-

Business Studies
-

Accountancy
-

Economics
-

Computer Science
-

Bio Technology
-

English
-

Enterprenership
-

Geography
-

Hindi
-

History
-

Home Science
-

Physical Education
-

Political Science
-

Psychology
-

Sociology
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Mathematics
-

Social Science
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Science
-

Social Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students

10th Standard Maths English Medium Model Question Paper Part - IV May-13 , 2020
10th Standard Maths English Medium Model Question Paper Part - IV
Model Question Paper Part - IV
10th Standard
-
Reg.No. :
Maths
Time :
02:30:00 Hrs
Total Marks :
100
-
If A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8} then state which of the following statement is true..
(a)(A x C) ⊂ (B x D)
(b)(B x D) ⊂ (A x C)
(c)(A x B) ⊂ (A x D)
(d)(D x A) ⊂ (B x A)
-
If f(x) = 2x2 and g(x) = \(\frac{1}{3x}\), then f o g is
(a)\(\\ \frac { 3 }{ 2x^{ 2 } } \)
(b)\(\\ \frac { 2 }{ 3x^{ 2 } } \)
(c)\(\\ \frac { 2 }{ 9x^{ 2 } } \)
(d)\(\\ \frac { 1 }{ 6x^{ 2 } } \)
-
If the HCF of 65 and 117 is expressible in the form of 65m - 117 , then the value of m is
(a)4
(b)2
(c)1
(d)3
-
The sum of first n terms of the series a, 3a, 5a...is ____________
(a)na
(b)(2n - 1)a
(c)n2 - a
(d)n2a2
-
Find the matrix X if 2X + \(\left( \begin{matrix} 1 & 3 \\ 5 & 7 \end{matrix} \right) =\left( \begin{matrix} 5 & 7 \\ 9 & 5 \end{matrix} \right) \)
(a)\(\left(\begin{array}{cc} -2 & -2 \\ 2 & -1 \end{array}\right)\)
(b)\(\left(\begin{array}{cc} 2 & 2 \\ 2 & -1 \end{array}\right)\)
(c)\(\left(\begin{array}{ll} 1 & 2 \\ 2 & 2 \end{array}\right)\)
(d)\(\left(\begin{array}{ll} 2 & 1 \\ 2 & 2 \end{array}\right)\)
-
In a \(\triangle\)ABC, AD is the bisector \(\angle\)BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. The length of the side AC is
(a)6 cm
(b)4 cm
(c)3 cm
(d)8 cm
-
In the adjacent figure \(\angle BAC\) = 90o and AD\(\bot \)BC then
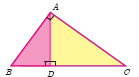 (a)
(a)BD.CD = BC2
(b)AB.AC = BC2
(c)BD.CD = AD2
(d)AB.AC = AD2
-
The point of intersection of 3x − y = 4 and x + y = 8 is
(a)(5, 3)
(b)(2, 4)
(c)(3, 5)
(d)(4, 4)
-
If sin \(\theta \) + cos\(\theta \) = a and sec \(\theta \) + cosec \(\theta \) = b, then the value of b(a2 - 1) is equal to
(a)2a
(b)3a
(c)0
(d)2ab
-
If the ratio of the height of a tower and the length of its shadow is \(\sqrt{3}: 1\), then the angle of elevation of the sun has measure
(a)45°
(b)30°
(c)90°
(d)60°
-
If x = a sec θ and = b tan θ, then b2x2 - a2y2 is equal to ___________
(a)ab
(b)a2-b2
(c)a2+b2
(d)a2b2
-
The volume (in cm3) of the greatest sphere that can be cut off from a cylindrical log of wood of base radius 1 cm and height 5 cm is
(a)\(\frac{4}{3}\pi\)
(b)\(\frac{10}{3}\pi\)
(c)\(5\pi\)
(d)\(\frac{20}{3}\pi\)
-
If the mean and coefficient of variation of a data are 4 and 87.5% then the standard deviation is
(a)3.5
(b)3
(c)4.5
(d)2.5
-
If are event occurs surely, then its probability is ___________
(a)0
(b)1
(c)\(\frac{1}{2}\)
(d)\(\frac{3}{4}\)
-
Represent the function f = {(1,2),(2,2),(3,2),(4,3),(5,4)} through
(i) an arrow diagram
(ii) a table form
(iii) a graph -
Find the 19th term of an A.P. -11, -15, -19,....
-
Prove that \(\sqrt { 3 } \) is irrational
-
Multiply \(\frac { { x }^{ 4 }{ b }^{ 2 } }{ x-1 } \) by \(\frac { { x }^{ 2 }-1 }{ { a }^{ 4 }{ b }^{ 3 } } \)
-
Solve the following system of linear equations in three variables.
x + y + z = 6; 2x + 3y + 4z = 20;
3x + 2y + 5z = 22 -
In the figure, AD is the bisector of \(\angle\)A. If BD = 4 cm, DC = 3 cm and AB = 6 cm, find AC.
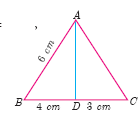
-
In figure if PQ || RS Prove that \(\Delta POQ\sim \Delta SOQ\)
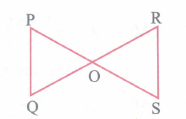
-
In each of the following, Find the value of ‘a’ for which the given points are collinear. (2, 3), (4, a) and (6, –3)
-
Show that the points (1, 7), (4, 2), (-1,-1) and (-4,4) are the vertices of a square.
-
The horizontal distance between two buildings is 70 m. The angle of depression of the top of the first building when seen from the top of the second building is 45°. If the height of the second building is 120 m, find the height of the first building.
-
A cone of height 24 cm is made up of modeling clay. A child reshapes it in the form of a cylinder of same radius as cone. Find the height of the cylinder.
-
Find the depth of a cylindrical tank of radius 28 m, if its capacity is equal to that of a rectangular tank of size 28 m x 16 m x 11 m.
-
Find the range and coefficient of range of the following data.
43.5, 13.6, 18.9, 38.4, 61.4, 29.8 -
Find the standard deviation for the following data. 5, 10, 15, 20, 25. And also find the new S.D. if three is added to each value.
-
Let A = {x \(\in \) W| x < 2}, B = {x \(\in \) N| 1 < x ≤ 4} and C = (3,5). Verify that
(A U B) x C = (A x C) U (B x C) -
A function f: (1,6) \(\rightarrow\)R is defined as follows:
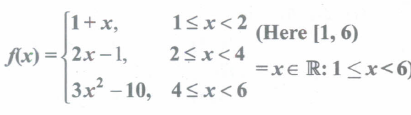
Find the value of f(3), -
Find the least number that is divisible by the first ten natural numbers.
-
Which of the following list of numbers form an AP? If they form an AP, write the next two terms:
-2, 2, -2, 2, -2 -
Iniya bought 50 kg of fruits consisting of apples and bananas. She paid twice as much per kg for the apple as she did for the banana. If Iniya bought Rs. 1800 worth of apples and Rs. 600 worth bananas, then how many kgs of each fruit did she buy?
-
BL and CM are medians of a triangle ABC right angled at A.
Prove that 4(BL2 + CM2) = 5BC2. -
Find the equation of the median and altitude of Δ ABC through A where the vertices are A(6, 2), B(-5,-1) and C(1, 9)
-
If the points A(6, 1), B(8, 2), C(9, 4) and D(P, 3) are the vertices of a parallelogram, taken in order. Find the value of P.
-
prove the following identities.
sec6\(\theta \) = tan6\(\theta \) + 3tan2\(\theta \)sec2\(\theta \) + 1 -
If sin (A - B) = \(\frac12\), cos (A + B) = \(\frac12\), 0o < A + ≤ 90°, A > B, find A and B.
-
If the radii of the circular ends of a frustum which is 45 cm high are 28 cm and 7 cm, find the volume of the frustum.
-
What is the ratio of the volume of a cylinder, a cone, and a sphere. If each has the same diameter and same height?
-
In a box there are 20 non-defective and some defective bulbs. If the probability that a bulb selected at random from the box found to be defective is \(\frac{3}{8}\) then, find the number of defective bulbs.
-
Find the co-efficient of variation for the following data: 16, 13, 17,21, 18.
-
-
Draw the graph of y = x2 + 3x + 2 and use it to solve x2 + 2x + 1 = 0
-
Discuss the nature of solutions of the following quadratic equations.
x2 + 2x + 5 = 0
-
-
-
Construct a \(\triangle\)PQR such that QR = 6.5 cm,\(\angle\)P = 60oand the altitude from P to QR is of length 4.5 cm.
-
Draw the two tangents from a point which is 5 cm away from the centre of a circle of diameter 6 cm. Also, measure the lengths of the tangents
-
Part I
Answer all the questions.
Choose the most suitable answer from the given four alternatives and write the option code with the corresponding answer.
14 x 1 = 14
Part II
Answer any 10 questions. Question no. 28 is compulsory.
10 x 2 = 20
Part III
Answer any 10 questions. Question no. 42 is compulsory.
10 x 5 = 50
Part IV
Answer all the questions.
2 x 8 = 16






 10th Standard Maths Syllabus
10th Standard Maths Syllabus  10th Standard Maths Study Materials
10th Standard Maths Study Materials

Reviews & Comments about 10th Standard Maths English Medium Model Question Paper Part - IV
Write your Comment