- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Physics
-

Chemistry
-

Maths
-

Accountancy
-

Introductory Micro and Macroeconomics
-

Business Studies
-

Economics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Tamil
-

Bio Technology
-

Engineering Graphics
-

Entrepreneurship
-

Hindi Core
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Political Science
-

Psychology
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Mathematics
-

Chemistry
-

Biology
-

Physics
-

Business Studies
-

Accountancy
-

Economics
-

Computer Science
-

Bio Technology
-

English
-

Enterprenership
-

Geography
-

Hindi
-

History
-

Home Science
-

Physical Education
-

Political Science
-

Psychology
-

Sociology
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Mathematics
-

Social Science
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Science
-

Social Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students

10th Standard Maths English Medium Public Exam Model Question Paper July 2020 May-09 , 2020
10th Standard Maths English Medium Public Exam Model Question Paper July 2020
Public Exam Important Questions July 2020
10th Standard
-
Reg.No. :
Maths
Time :
03:00:00 Hrs
Total Marks :
100
-
If the ordered pairs (a + 2, 4) and (5, 2a + b) are equal then (a, b) is
(a)(2,-2)
(b)(5,1)
(c)(2,3)
(d)(3,-2)
-
If f(x) = 2x2 and g(x) = \(\frac{1}{3x}\), then f o g is
(a)\(\\ \frac { 3 }{ 2x^{ 2 } } \)
(b)\(\\ \frac { 2 }{ 3x^{ 2 } } \)
(c)\(\\ \frac { 2 }{ 9x^{ 2 } } \)
(d)\(\\ \frac { 1 }{ 6x^{ 2 } } \)
-
If the order pairs (a, -1) and (5, b) belongs to {(x, y) | y = 2x + 3}, then a and b are __________
(a)-13, 2
(b)2, 13
(c)2, -13
(d)-2,13
-
If f(x) = mx + n, when m and n are integers f(-2) = 7, and f(3) = 2 then m and n are equal to ___________
(a)-1, -5
(b)1, -9
(c)-1, 5
(d)1, 9
-
If f(x) = ax - 2, g(x) = 2x - 1 and fog = gof, the value of a is ___________
(a)3
(b)-3
(c)\(\frac { 1 }{ 3 } \)
(d)13
-
If f(x) + f(1 - x) = 2 then \(f\left( \frac { 1 }{ 2 } \right) \) is ___________
(a)5
(b)-1
(c)-9
(d)1
-
The sum of the exponents of the prime factors in the prime factorization of 1729 is
(a)1
(b)2
(c)3
(d)4
-
Given F1 = 1, F2 = 3 and Fn = Fn-1 + Fn-2 then F5 is
(a)3
(b)5
(c)8
(d)11
-
If 3 is the least prime factor of number 'a' and 7 is least prime factor of number 'b', then the least prime factor of a + b is ____________
(a)a + b
(b)2
(c)5
(d)10
-
Sum of first n terms of the series \(\sqrt { 2 } +\sqrt { 8 } +\sqrt { 18 } +...\) is ____________
(a)\(\frac { n(n+1) }{ 2 } \)
(b)\(\sqrt { n } \)
(c)\(\frac { n\left( n+1 \right) }{ \sqrt { 2 } } \)
(d)1
-
If (x - 6) is the HCF of x2 - 2x - 24 and x2 - kx - 6 then the value of k is
(a)3
(b)5
(c)6
(d)8
-
If A = \(\left( \begin{matrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{matrix} \right) \), B = \(\left( \begin{matrix} 1 & 0 \\ 2 & -1 \\ 0 & 2 \end{matrix} \right) \) and C = \(\left( \begin{matrix} 0 & 1 \\ -2 & 5 \end{matrix} \right) \), Which of the following statements are correct?
(i) AB + C = \(\left( \begin{matrix} 5 & 5 \\ 5 & 5 \end{matrix} \right) \)
(ii) BC = \(\left( \begin{matrix} 0 & 1 \\ 2 & -3 \\ -4 & 10 \end{matrix} \right) \)
(iii) BA + C = \(\left( \begin{matrix} 2 & 5 \\ 3 & 0 \end{matrix} \right) \)
(iv) (AB)C = \(\left( \begin{matrix} -8 & 20 \\ -8 & 13 \end{matrix} \right) \)(a)(i) and (ii) only
(b)(ii) and (iii) only
(c)(iii) and (iv) only
(d)all of these
-
Which of the following are linear equation in three variables ___________
(a)2x = z
(b)2sin x + y cos y + z tan z = 2
(c)x + 2y2 + z = 3
(d)x - y - z = 7
-
For what set of values \(\frac { { x }^{ 2 }+5x+6 }{ { x }^{ 2 }+8x+15 } \) is undefined ___________
(a)-3, -5
(b)-5
(c)-2, -3, -5
(d)-2, -3
-
Choose the correct answer
(i) Every scalar matrix is an identity matrix
(ii) Every identity matrix is a scalar matrix
(iii) Every diagonal matrix is an identity matrix
(iv) Every null matrix is a scalar matrix(a)(i) and (iii) only
(b)(iii) only
(c)(iv) only
(d)(ii) and (iv) only
-
If \(\triangle\)ABC is an isosceles triangle with \(\angle\)C = 90o and AC = 5 cm, then AB is
(a)2.5 cm
(b)5 cm
(c)10 cm
(d)\(5\sqrt { 2 } \)cm
-
The two tangents from an external points P to a circle with centre at O are PA and PB. If \(\angle APB\) = 70o then the value of \(\angle AOB\) is
(a)100°
(b)110°
(c)120°
(d)130°
-
In the given figure DE||BC:BD = x - 3, BA = 2x,CE = x- 2, and AC = 2x + 3, Find the value of x.
(a)3
(b)6
(c)9
(d)12
-
In a triangle, the internal bisector of an angle bisects the opposite side. Find the nature of the triangle.
(a)right angle
(b)equilateral
(c)scalene
(d)isosceles
-
The perimeter of a right triangle is 36 cm. Its hypotenuse is 15 cm, then the area of the triangle is ____________
(a)108 cm2
(b)54 cm2
(c)27 cm2
(d)216 cm2
-
If slope of the line PQ is \(\frac { 1 }{ \sqrt { 3 } } \) then slope of the perpendicular bisector of PQ is
(a)\(\sqrt { 3 } \)
(b)\(-\sqrt { 3 } \)
(c)\(\frac { 1 }{ \sqrt { 3 } } \)
(d)0
-
When proving that a quadrilateral is a trapezium, it is necessary to show
(a)Two sides are parallel
(b)Two parallel and two non-parallel sides
(c)Opposite sides are parallel
(d)All sides are of equal length
-
Find the slope of the line 2y = x + 8 ____________
(a)\(\frac { 1 }{ 2 } \)
(b)1
(c)8
(d)2
-
Find the value of P, given that the line \(\frac { y }{ 2 } =x-p\) passes through the point (-4, 4) is ____________
(a)-4
(b)-6
(c)0
(d)8
-
If sin \(\theta \) + cos\(\theta \) = a and sec \(\theta \) + cosec \(\theta \) = b, then the value of b(a2 - 1) is equal to
(a)2a
(b)3a
(c)0
(d)2ab
-
Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is
(a)\(\sqrt { 2 } \) x
(b)\(\frac { x }{ 2\sqrt { 2 } } \)
(c)\(\frac { x }{ \sqrt { 2 } } \)
(d)2x
-
If A is an assets angle of Δ ABC, right angle at 3, then the value of sin A T cos A is ___________
(a)=1
(b)>1
(c)<1
(d)=2
-
The value of sin2 θ + \(\frac { 1 }{ 1+{ tan }^{ 2 }\theta } \) of ___________
(a)sin2θ
(b)cos2θ
(c)secθ
(d)1
-
The blanks of river are parallel. A swimmer starts from a point on one of the banks and swims in a straight line to the bank at 45o and reaches the opposite bank at a point 20 m, from the point opposite to the straight point. The breadth of the river is equal to ____________
(a)12.12m
(b)14.14m
(c)1016.16m
(d)18.18m
-
If the radius of the base of a right circular cylinder is halved keeping the same height, then the ratio of the volume of the cylinder thus obtained to the volume of original cylinder is
(a)1:2
(b)1:4
(c)1:6
(d)1:8
-
In a hollow cylinder, the sum of the external and internal radii is 14 cm and the width is 4 cm. If its height is 20 cm, the volume of the material in it is
(a)5600\(\pi\) cm3
(b)1120\(\pi\) cm3
(c)56\(\pi\) cm3
(d)3600\(\pi\) cm3
-
How many balls, each of radius 1 cm, can be made from a solid sphere of lead of radius cm?
(a)64
(b)216
(c)512
(d)16
-
The curved surface area of a cylinder is 264 cm2 and its volume is 924 cm2. The ratio of diameter to its height is ___________
(a)3:7
(b)7:3
(c)6:7
(d)7:6
-
If a letter is chosen at random from the English alphabets {a, b....,z}, then the probability that the letter chosen precedes x ____________
(a)\(\frac { 12 }{ 13 } \)
(b)\(\frac { 1 }{ 13 } \)
(c)\(\frac { 23 }{ 26 } \)
(d)\(\frac { 3 }{ 26 } \)
-
Which of the following is not a measure of dispersion?
(a)Range
(b)Standard deviation
(c)Arithmetic mean
(d)Variance
-
The mean of 100 observations is 40 and their standard deviation is 3. The sum of squares of all observations is
(a)40000
(b)160900
(c)160000
(d)30000
-
A girl calculates the probability of her winning in a match is 0.08 what is the probability of her losing the game ___________
(a)91%
(b)8%
(c)92%
(d)80%
-
If the standard deviation of a variable x is 4 and if = \(\frac { 3x+5 }{ 4 } \) , then the standard deviation of y is ___________
(a)4
(b)3.5
(c)3
(d)2.5
-
If an event occurs surely, then its probability is _________.
(a)1
(b)0
(c)\(\frac { 1 }{ 2 } \)
(d)\(\frac { 3 }{ 4 } \)
-
A Relation R is given by the set {(x, y) / y = x + 3, x \(\in \) {0, 1, 2, 3, 4, 5}}. Determine its domain and range.
-
Using the functions f and g given below, find f o g and g o f. Check whether f o g = g o f.
f(x) = x - 6, g(x) = x2 -
Let A = {1,2, 3, 4} and B = {-1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12} Let R = {(1, 3), (2, 6), (3, 10), (4, 9)} \(\subseteq \) A x B be a relation. Show that R is a function and find its domain, co-domain and the range of R.
-
Let A = {0, 1, 2, 3} and B = {1, 3, 5, 7, 9} be two sets. Let f: A \(\rightarrow\)B be a function given by f(x) = 2x + 1. Represent this function as a table.
-
Let A = {0, 1, 2, 3} and B = {1, 3, 5, 7, 9} be two sets. Let f: A \(\rightarrow\)B be a function given by f(x) = 2x + 1. Represent this function as a graph.
-
Find the least positive value of x such that
67 + x \(\equiv \) 1 (mod 4) -
Which of the following sequences are in G.P.?
0.5, 0.05, 0.005,…, -
Write down the quadratic equation in general form for which sum and product of the roots are given below.
9, 14 -
Determine the nature of roots for the following quadratic equation. 2x2 - x - 1 = 0
-
Show that \(\triangle\) PST~\(\triangle\) PQR
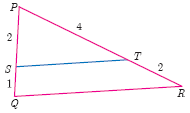
-
Two triangles QPR and QSR, right angled at P and S respectively are drawn on the same base QR and on the same side of QR. If PR and SQ intersect at T, prove that PT x TR = ST x TQ. \(\triangle\)
-
What is the slope of a line perpendicular to the line joining A(5, 1) and P where P is the mid-point of the segment joining (4, 2) and (-6, 4).
-
Find the equation of a straight line passing through (5, - 3) and (7, - 4).
-
Find the value of ‘a’, if the line through (–2, 3) and (8, 5) is perpendicular to y = ax + 2
-
prove that \(\sqrt { \frac { 1+cos\theta }{ 1-cos\theta } } \) = cosec \(\theta \) + cot\(\theta \)
-
prove the following identity tan4\(\theta \) + tan2\(\theta \) = sec4\(\theta \) - sec2\(\theta \) .
-
A 14 m deep well with inner diameter 10 m is dug and the earth taken out is evenly spread all around the well to form an embankment of width 5 m. Find the height of the embankment.
-
A metallic sphere of radius 16 cm is melted and recast into small spheres each of radius 2 cm. How many small spheres can be obtained?
-
Calculate the range of the following data..
Income 400-450 450-500 500-550 550-600 600-650 Number of workers 8 12 30 21 6 -
The standard deviation and mean of a data are 6.5 and 12.5 respectively. Find the coefficient of variation.
-
A function f: [-7,6) \(\rightarrow\) R is defined as follows.
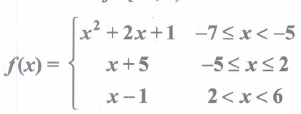
f(-7) - f(-3) -
A function f: (1,6) \(\rightarrow\)R is defined as follows:
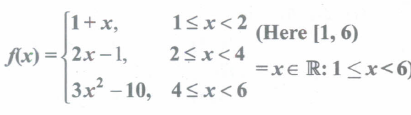
Find the value of f(2) - f( 4). -
Which of the following list of numbers form an AP? If they form an AP, write the next two terms:
1,-1,-3, -5, ... -
The number of seats in a row is equal to the total number of rows in a hall. The total number of seats in the hall will increase by 375 if the number of rows is doubled and the number of seats in each row is reduced by 5. Find the number of rows in the hall at the beginning.
-
Find the sum and product of the roots for each of the following quadratic equations:
kx2 - k2x - 2k3 = 0 -
Solve the following quadratic equations by formula method
36y2 - 12ay + (a2 - b2) = 0 -
Seven years ago, Varun's age was five times the square of Swati's age. Three years hence Swati's age will be two fifth of Varun's age. Find their present ages.
-
Construct a triangle similar to a given triangle PQR with its sides equal to \(\frac{3}{5}\) of the corresponding sides of the triangle PQR (scale factor \(\frac { 3 }{ 5 } <1\))
-
In figure \(\angle\)QPR = 90o, PS is its bisector. If ST\(\bot \)PR, prove that ST \(\times\) (PQ + PR) = PQ \(\times\) PR.
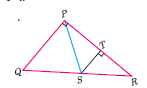
-
Find the value of k, if the area of a quadrilateral is 28 sq. units, whose vertices are (–4, –2), (–3, k), (3, –2) and (2, 3)
-
As shown in the figure, Two trees are standing on the flat ground. the angel of elevation of the top of both the trees from a point x on the ground is 40° .if the horizontal distance between x and the smaller tree is 8m and the distance of the top of the trees is 20m, calculate, the distance between the point x and the top of the smaller tree.
-
A vertical pole fixed to the ground is divided in the ratio 1:9 by a mark on it with lower part shorter than the upper part. If the two parts subtend equal angles at a place on the ground, 25 m away from the base of the pole, what is the height of the pole?
-
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats.(\( \sqrt { 3 } \) = 1.732)
-
If sin 3A = cos (A - 26°), where 3A is an acute angle, find the value at A.
-
A container open at the top is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends are 8 cm and 20 cm respectively. Find the cost of milk which can completely fill a container at the rate of Rs. 40 per litre.
-
A vessel is in the form of a hemispherical bowl mounted by a hollow cylinder. The diameter is 14 cm and the height of the vessel is 13 cm. Find the capacity of the vessel.
-
A hollow metallic cylinder whose external radius is 4.3 cm and internal radius is 1.1 cm and whole length is 4 cm is melted and recast into a solid cylinder of 12 cm long. Find the diameter of solid cylinder.
-
A teacher asked the students to complete 60 pages of a record note book. Eight students have completed only 32, 35, 37, 30, 33, 36, 35 and 37 pages. Find the standard deviation of the pages yet to be completed by them.
-
A bag contains 5 blue balls and 4 green balls. A ball is drawn at random from the bag. Find the probability that the ball drawn is (i) blue (ii) not blue.
-
If for a distribution \( \Sigma (x-5)=3,\Sigma (x-5)^{ 2 }\), and total number of observations is 18, find the mean and standard deviation.
-
Construct a \(\triangle\)PQR such that QR = 6.5 cm,\(\angle\)P = 60oand the altitude from P to QR is of length 4.5 cm.
-
Draw the two tangents from a point which is 5 cm away from the centre of a circle of diameter 6 cm. Also, measure the lengths of the tangents
Part A
40 x 1 = 40
Part B
20 x 2 = 40
Part C
20 x 5 = 100
Part D
2 x 8 = 16






 10th Standard Maths Syllabus
10th Standard Maths Syllabus  10th Standard Maths Study Materials
10th Standard Maths Study Materials

Reviews & Comments about 10th Standard Maths English Medium Public Exam Model Question Paper July 2020
Write your Comment