Let f(x) = \(\sqrt { 1+x^{ 2 } } \) then

f(x) = (x + 1)³ - (x - 1)³ represents a function which is

The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is

How many terms are there in the G.P : 5, 20, 80, 320,..., 20480

Which of the following should be added to make x⁴ + 64 a perfect square

The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is

Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?

The equation of a line passing through the origin and perpendicular to the line 7x - 3y + 4 = 0 is

If sin \(\theta \) = cos \(\theta \), then 2 tan² \(\theta \) + sin² \(\theta \) -1 is equal to 

The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is

Given that sin ∝ = \(\frac{1}{2}\) and cos β = \(\frac{1}{2}\), then the value of (∝ + β) is ___________

A spherical ball of radius r₁ units is melted to make 8 new identical balls each of radius r₂ units. Then r₁:r₂ is

A purse contains 10 notes of Rs. 2000, 15 notes of Rs. 500, and 25 notes of Rs. 200. One note is drawn at random. What is the probability that the note is either a Rs. 500 note or Rs. 200 note?

A number x is chosen at random from -4, -3, -2, -1, 0, 1, 2, 3, 4 find the probability that |x| ≤ 4

Find k, if f(k) = 2k - 1 and f o f(k) = 5.

First term a and common difference d are given below. Find the corresponding A.P
a = 5, d = 6

Find the LCM and HCF of 6 and 20 by the prime factorisation method.

Find the values of x, y, z if
\(\left[ \begin{matrix} x & y-z & z+3 \end{matrix} \right] +\left[ \begin{matrix} y & 4 & 3 \end{matrix} \right] =\left[ \begin{matrix} 4 & 8 & 16 \end{matrix} \right] \)

Using quadratic formula solve the following equations.9x²-9(a+b)x+(2a²+5ab+2b²)=0

In fig. if PQ || BC and PR || CD prove that

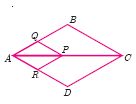
\(\frac { QB }{ AQ } =\frac { DR }{ AR } \)

In figure if PQ || RS Prove that \(\Delta POQ\sim \Delta SOQ\)

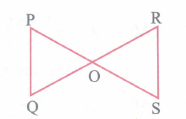
What is the inclination of a line whose slope is 0

If A (-5, 7), B (-4, -5), C (-1, -6) and D (4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.

prove that 1+\(\frac { co{ t }^{ 2 }\theta }{ 1+cosec\theta } \) = cosec\(\theta \) 

If the total surface area of a cone of radius 7cm is 704 cm², then find its slant height.

If the radii of the circular ends of a conical bucket which is 45 cm high are 28 cm and 7 cm, find the capacity of the bucket. (Use π = \(\frac{22}{7}\))

The following table gives the values of mean and variance of heights and weights of the 10th standard students of a school.

Which is more varying than the other?

The marks scored by 5 students in a test for 50 marks are 20, 25, 30, 35, 40. Find the S.D for the marks. If the marks are converted for 100 marks, find the S.D. for newly obtained marks.

If the function f is defined by
\(f(x)= \begin{cases}x+2 & \text { if } x>1 \\ 2 & \text { if }-1 \leq x \leq 1 \\ x-1 & \text { if }-3<x<-1\end{cases}\)
find the values of
i) f(3)
ii) f(0)
iii) f(-1.5)
iv) f(2) + f(-2)

A functionf: (1,6) \(\rightarrow\)R is defined as follows:

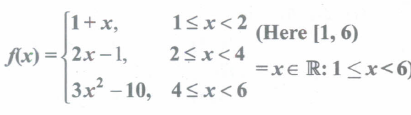
Find the value of f(5),

A man saved Rs.16500 in ten years. In each year after the first he saved Rs.100 more than he did in the preceding year. How much did he save in the first year?

Which of the following list of numbers form an AP? If they form an AP, write the next two terms:
-2, 2, -2, 2, -2

If A = \(\left[ \begin{matrix} 1 & -1 & 2 \end{matrix} \right] \), B = \(\left[ \begin{matrix} 1 & -1 \\ 2 & 1 \\ 1 & 3 \end{matrix} \right] \) and C = \(\left[ \begin{matrix} 1 & 2 \\ 2 & -1 \end{matrix} \right] \) show that (AB)C = A(BC)

In \(\angle ACD={ 90 }^{ 0 }\) and \(CD\bot AB\) Prove that \(\cfrac { { BC }^{ 2 } }{ { AC }^{ 2 } } =\cfrac { BD }{ AD } \)

Find the equation of a straight line Passing through (1, -4) and has intercepts which are in the ratio 2:5

If the points A(6, 1), B(8, 2), C(9, 4) and D(P, 3) are the vertices of a parallelogram, taken in order. Find the value of P.

show that \(\left( \frac { 1+ta{ n }^{ 2 }A }{ 1+co{ t }^{ 2 }A } \right) ={ \left( \frac { 1-ta{ nA } }{ 1-cotA } \right) }^{ 2 }\) 

If 15tan² θ+4 sec² θ=23 then find the value of (secθ+cosecθ)² -sin² θ

From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and base is hollowed out. Find the total surface area of the remaining solid.

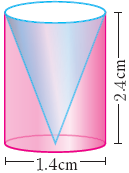
A spherical ball of iron has been melted and made into small balls. If the radius of each smaller ball is one-fourth of the radius of the original one, how many such balls can be made?

A bag contains 12 blue balls and x red balls. If one ball is drawn at random (i) what is the probability that it will be a red ball? (ii) If 8 more red balls are put in the bag, and if the probability of drawing a red ball will be twice that of the probability in (i), then find x.

C.V. of a data is 69%, S.D. is 15.6, then find its mean.