- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Physics
-

Chemistry
-

Maths
-

Accountancy
-

Introductory Micro and Macroeconomics
-

Business Studies
-

Economics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Tamil
-

Bio Technology
-

Engineering Graphics
-

Entrepreneurship
-

Hindi Core
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Political Science
-

Psychology
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Mathematics
-

Chemistry
-

Biology
-

Physics
-

Business Studies
-

Accountancy
-

Economics
-

Computer Science
-

Bio Technology
-

English
-

Enterprenership
-

Geography
-

Hindi
-

History
-

Home Science
-

Physical Education
-

Political Science
-

Psychology
-

Sociology
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Mathematics
-

Social Science
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Science
-

Social Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students
Sets, Relations and Functions Important Question Paper
11th Standard
-
Reg.No. :
Mathematics
Time :
01:00:00 Hrs
Total Marks :
50
-
The number of constant functions from a set containing m elements to a set containing n elements is
(a)mn
(b)m
(c)n
(d)m+n
-
The function f:[0,2π]➝[-1,1] defined by f(x) = sin x is
(a)one-to-one
(b)on to
(c)bijection
(d)cannot be defined
-
If the function f:[-3,3]➝S defined by f(x) = x2 is onto, then S is
(a)[-9,9]
(b)R
(c)[-3,3]
(d)[0,9]
-
Given A = {5,6,7,8}. Which one of the following is incorrect?
(a)Ø ⊆ A
(b)A⊆A
(c){7,8,9}⊆A
(d){5}⊆A
-
The shaded region in the adjoining diagram represents.
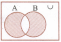 (a)
(a)A\B
(b)B\A
(c)AΔB
(d)A'
-
Write the following in roster form {x\(\in \)N : 4x + 9 < 52}
-
Write the following in roster form.
\(\left\{ x:\frac { x-4 }{ x+2 } =3,x\in R-\{ -2\} \right\} \) -
The total cost of airfare on a given route is comprised of the base cost C and the fuel surcharge S in rupee. Both C and S functions of the mileage m; C(m) = 0.4m + 50 and S(m) = 0.03m. Determine a function for the total cost of a ticket in terms of the mileage and find the airfare for flying 1600 miles.
-
Check whether the following sets are disjoint where p = {x : x is a prime < 15} and Q = {x : x is a multiple of 2 and x < 16}
-
If U = {x : 1 ≤ x ≤ 10, x ∈ N}, A = {1, 3, 5, 7, 9} and B = {2, 3, 5, 9, 10} then find A'UB'.
-
Graph the function f(x) = x3 and \(g(x)=\sqrt[3]x\) on the same co-ordinate plane. Find f o g and graph it on the plane as well. Explain your results.
-
Write the steps to obtain the graph of the function y = 3(x-1)2+5 from the graph y = x2
-
By taking suitable sets A, B, C, verify the following results:
A \(\times\) (B\(\cap \)C) = (A\(\times\)B) \(\cap \) (A\(\times\)C) -
Find the pairs of equal sets from the following sets. A = {0}, B = {x : x > 15 and x < 5}, C = {x : x - 5 = 0}, D = {x : x2 = 25}, E = {x : x is an integral positive root of the equation x2 - 2x - 15 = 0}.
-
Which of the following sets are finite and which are infinite?
Set of concentric circles in a plane. -
The formula for converting from Fahrenheit to Celsius temperatures is \(y={5x\over 9}-{160\over 9}\). Find the inverse of this function and determine whether the inverse is also a function.
-
A simple cipher takes a number and codes it, using the function f(x) = 3x - 4. Find the inverse of this function, determine whether the inverse is also a function and verify the symmetrical property about the line y = x(by drawing the lines)
-
The cartesian product A \(\times\) A has 9 elements among which are found (-1, 0) and (0, 1).Find the set A and the remaining elements of A \(\times\)A.
-
Show that the relation R on the set R of all real numbers defined as R = {(a, b): a < b2} is neither reflexive, nor symmetric nor transitive.
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
4 x 5 = 20
*****************************************
11th Standard Maths Videos
TN 9th Maths Mensuration Important 2 Marks Questions With Answers Book Back and Creative
TN Class 9th Maths Mensuration Study Materials TN State Board / Matriculation 9th Maths Subject - Mensuration Two Mark Question and Answers






 11th Standard Maths Syllabus
11th Standard Maths Syllabus  11th Standard Maths Study Materials
11th Standard Maths Study Materials 11th Standard Maths MCQ Practise Tests
11th Standard Maths MCQ Practise Tests 

Reviews & Comments about 11th Maths - Unit 1 Slip Test Question Paper
Write your Comment