The shaded region in the adjoining diagram represents.

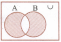(a)

A\B

(b)

B\A

(c)

AΔB

(d)

A'

For real numbers x and y, define xRy if x - y + √2 is an irrational number. Then the relation R is __________

(a)

reflexive

(b)

symmetric

(c)

transitive

(d)

none of these

The number of reflective relations one set containing n elements is __________

(a)

2¹²

(b)

2⁴

(c)

2¹⁶

(d)

2⁸

Which one of the following statements is false? The graph of the function \(f(x)={1\over x}\)

(a)

exist is the first and third quadrant only

(b)

is a reciprocal function

(c)

is defined at x = 0

(d)

it is symmetric about y = x and y = - x.

Which one of the following is not a singleton set?

(a)

A = {x : 3x - 5 = 0, x ∈ Q}

(b)

B = {| x | = 1 / x ∈ Z}

(c)

{x : x³ - 1 = 0, x ∈ R}

(d)

{x : 30x = 60, x ∈ N}

The rationalising factor of \(\frac { 5 }{ \sqrt [ 3 ]{ 3 } } \) is

(a)

\(\sqrt [ 3 ]{ 6 } \)

(b)

\(\sqrt [ 3 ]{ 3 } \)

(c)

\(\sqrt [ 3 ]{ 9 } \)

(d)

\(\sqrt [ 3 ]{ 27 } \)

The number of real solution of |2x - x²- 3| = 1 is ___________

(a)

0

(b)

2

(c)

3

(d)

4

(x²-2x+2)(x²+2x+2) are the factors of the polynomial ___________

(a)

(x²-2x)²

(b)

x⁴-4

(c)

x⁴+4

(d)

(x²-2x+2)²

Given \(|\frac{3}{x-4}|<1\) then ___________

(a)

x∈(∞,3)

(b)

x∈(4, ∞)

(c)

x∈(1, 7)

(d)

x∈(1, 4)U(4, 7)

Solve 3x² + 5x - 2≤0

(a)

(2,\(\frac{1}{3}\))

(b)

[2,\(\frac{1}{3}\)]

(c)

(-2,\(\frac{1}{3}\))

(d)

(-2,\(\frac{-1}{3}\))

Zero of the polynomial p(x) = x² - 4x + 4

(a)

1

(b)

2

(c)

-2

(d)

-1

The value of \(\sqrt [ 4 ]{ { (-2) }^{ 4 } } =\) _______.

(a)

2

(b)

-2

(c)

4

(d)

-4

If the angles of a triangle are in A.P., then the measure of one of the angles in radians is ___________

(a)

\(\frac { \pi }{ 6 } \)

(b)

\(\frac { \pi }{ 3 } \)

(c)

\(\frac { \pi }{ 2 } \)

(d)

\(\frac { 2\pi }{ 3 } \)

If tan x = \(\frac { -1 }{ \sqrt { 5 } } \) and x lies in the IV quadrant, then the value of cos x is ___________

(a)

\(\sqrt { \frac { 5 }{ 6 } } \)

(b)

\(\frac { 2 }{ \sqrt { 6 } } \)

(c)

\(\frac { 1 }{ 2 } \)

(d)

\(\frac { 1 }{ \sqrt { 6 } } \)

The value of sin²\(\frac { 5\pi }{ 12 } -sin^{ 2 }\frac { \pi }{ 12 } \) is ___________

(a)

\(\frac { 1 }{ 2 } \)

(b)

\(\frac { \sqrt { 3 } }{ 2 } \)

(c)

1

(d)

0

cos 35⁰ + cos 85⁰ + cos 155⁰ = _______________

(a)

0

(b)

\(\frac { 1 }{ \sqrt { 3 } } \)

(c)

\(\frac { 1 }{ \sqrt { 2 } } \)

(d)

cos 275⁰

2tan^-1\(\left( \frac { 1 }{ 5 } \right) \) is equal to _______________

(a)

tan\(\left( \frac { 5 }{ 12 } \right) \)

(b)

\(\frac { 5 }{ 12 } \)

(c)

\(\tan^{-1}\left({5 \over 12}\right)\)

(d)

tan^-1\(\frac { 2 }{ 5 } \)

If 2 sin θ + 1 = 0 and \(\sqrt{3}\) tan θ = 1, then the most general value of θ is _______________

(a)

\(n\pi\pm\frac{\pi}{6}\)

(b)

\(n\pi+(-1)^n\frac{7\pi}{6}\)

(c)

\(2n\pi+\frac{7\pi}{6}\)

(d)

\(2n\pi+\frac{11\pi}{6}\)

If ABCD is a cyclic quadrilateral then cos A + cos B + cos C + cos D = _______________

(a)

1

(b)

-1

(c)

0

(d)

None

\(\frac{1}{360}\) of a complete rotation clockwise is _______________

(a)

-1°

(b)

-360°

(c)

-90°

(d)

1°

Choose the incorrect pair:

(a)

sinx - x ∈ R

(b)

cos x - x ∈ R

(c)

log x x > 0

(d)

e^-x - x > 0

Choose the incorrect pair:

(a)

sin x in II^nd quadrant

(b)

cos x in I^st quadrant 1

(c)

sec x in II^st quadrant -2

(d)

tan x in III^rd quadrant20

Find the incorrect pair

(a)

\(\\ \frac { a }{ sin\ A } =\frac { b }{ sin\ B } =\frac { C }{ sin\ C } \) - 2R

(b)

\(\frac { { b }^{ 2 }+{ c }^{ 2 }-{ a }^{ 2 } }{ 2bc } \) - cos A

(c)

\(\frac { a-b }{ a+b } cot\frac { c }{ 2 } \) - tan\(\frac{A-B}{2}\)

(d)

\(\frac { { a }^{ 2 }+{ c }^{ 2 }-{ b }^{ 2 } }{ 2ac } \) - cos C

If mC₁ = nC₂, then _________

(a)

2m = n

(b)

2m = n(n+1)

(c)

2m = n(n-1)

(d)

2n=m(m-1)

Among the players 5 are bowlers. In how many ways a team of 11 may be formed with atleast 4 bowlers?

(a)

265

(b)

263

(c)

264

(d)

275