- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Physics
-

Chemistry
-

Maths
-

Accountancy
-

Introductory Micro and Macroeconomics
-

Business Studies
-

Economics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Tamil
-

Bio Technology
-

Engineering Graphics
-

Entrepreneurship
-

Hindi Core
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Political Science
-

Psychology
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Mathematics
-

Chemistry
-

Biology
-

Physics
-

Business Studies
-

Accountancy
-

Economics
-

Computer Science
-

Bio Technology
-

English
-

Enterprenership
-

Geography
-

Hindi
-

History
-

Home Science
-

Physical Education
-

Political Science
-

Psychology
-

Sociology
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Mathematics
-

Social Science
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Science
-

Social Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students

11th Standard Maths Public Exam Official Model Question Paper 2019 Mar-04 , 2019
+1 Public Official Model Question 2019
+1 Public Official Model Question 2019
11th Standard
-
Reg.No. :
Maths
Time :
02:30:00 Hrs
Total Marks :
90
-
The shaded region in the adjoining diagram represents.
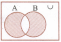 (a)
(a)A\B
(b)B\A
(c)AΔB
(d)A'
-
If n((A \(\times\) B) ∩(A \(\times\) C)) = 8 and n(B ∩ C) = 2, then n(A) is
(a)6
(b)4
(c)8
(d)16
-
The value of log3 11.log11 13.log13 15.log15 27.log27 81 is
(a)1
(b)2
(c)3
(d)4
-
The maximum value of 4sin2x + 3 cos2x + \(sin\frac { x }{ 2 } +cos\frac { x }{ 2 } \) is
(a)\(4 + \sqrt{2}\)
(b)\(3+ \sqrt{2}\)
(c)9
(d)4
-
The maximum value of 3 sin θ+4 cos θ is _______________
(a)1
(b)3
(c)4
(d)5
-
If (n+5)P(n+1)=\((\frac { 11(n-1) }{ 2 } )\).(n+3)Pn, then the value of n are
(a)7 and 11
(b)6 and 7
(c)2 and 11
(d)2 and 6
-
The number of ways to average the letters of the word CHEESE are _________
(a)120
(b)240
(c)720
(d)6
-
The sum up to n terms of the series \(\sqrt { 2 } +\sqrt { 8 } +\sqrt { 18 } +\sqrt { 32 } +\).....is
(a)\(\frac { n(n+1) }{ 2 } \)
(b)2n(n+1)
(c)\(\frac { n(n+1) }{ \sqrt { 2 } } \)
(d)1
-
Slope of x-axis or a line parallel to x-axis is ______________
(a)0
(b)positive
(c)negative
(d)infinity
-
The lines x cos \(\alpha\) + y sin \(\alpha\) = p and xcos\(\beta\) + y sin\(\beta\) = q will be perpendicular if ______________
(a)\(\alpha =\beta\)
(b)\(\alpha-\beta=\frac{\pi}{2}\)
(c)\(|\alpha-\beta|=\frac{\pi}{2}\)
(d)\(\alpha-\beta=0\)
-
If x1, x2, x3 as well as y1, y2, y3 are in geometric progression with the same common ratio, then the points (x1, y1 ), (x2, y2), (x3, y3 ) are
(a)vertices of an equilateral triangle
(b)vertices of a right angled triangle
(c)vertices of a right angled isosceles triangle
(d)collinear
-
A matrix which is not a square matrix is called a_________matrix.
(a)singular
(b)non-singular
(c)non-square
(d)rectangular
-
If \(|\overrightarrow { a } |=10,|\overrightarrow { b } |=2,\) and \(|\overrightarrow { a } .\overrightarrow { b } |=12\) then the value of \(|\overrightarrow { a } \times \overrightarrow { b } |\) is ___________ .
(a)5
(b)10
(c)14
(d)16
-
\(lim_{x \rightarrow \infty}{\sqrt{x^2-1}\over 2x+1}=\)
(a)1
(b)0
(c)-1
(d)\(1\over 2\)
-
For what values of x is the rate of increase of x3 - 2x2 + 3x + 8 is twice the rate of increase of x?
(a)\(\left( -\frac { 1 }{ 3 } ,-3 \right) \)
(b)\(\left( \frac { 1 }{ 3 } ,3 \right) \)
(c)\(\left( -\frac { 1 }{ 3 } ,3 \right) \)
(d)\(\left( \frac { 1 }{ 3 } ,1 \right) \)
-
The derivative of f(x) = x |x| at x = −3 is
(a)6
(b)-6
(c)does not exist
(d)0
-
\(\int e^{-4 x} \cos x d x\) is
(a)\({e^{-4x}\over 17}[4cos \ x-sin \ x]+c\)
(b)\({e^{-4x}\over 17}[-4cos \ x+sin \ x]+c\)
(c)\({e^{-4x}\over 17}[4cos \ x+sin \ x]+c\)
(d)\({e^{-4x}\over 17}[-4cos \ x-sin \ x]+c\)
-
\(\int { \frac { 4\left( sin^{ -1 }x \right) ^{ 3 } }{ \sqrt { 1-{ x }^{ 2 } } } } \) dx = ________+c.
(a)log (sin -1x)
(b)(sin -1 x)4
(c)4 (sin-1 x)4
(d)\(\frac { \left( { sin }^{ -1 }x \right) ^{ 4 } }{ 4 } \)
-
If A and B are two events such that A ⊂ B and P(B)\(\neq o\), then which of the following is correct?
(a)\(P(A/B)={P(A)\over P(B)}\)
(b)P(A/B)
(c)P(A/B)\(\ge\)P(A)
(d)P(A/B)>P(B)
-
Out of 30 consecutive integers, 2 are chosen at random. The probability that their sum is odd is
(a)\(\frac { 14 }{ 29 } \)
(b)\(\frac { 16 }{ 29 } \)
(c)\(\frac { 15 }{ 29 } \)
(d)\(\frac { 10 }{ 29 } \)
-
On the set of natural number let R be the relation defined by aRb if a + b \(\le\) 6. Write down the relation by listing all the pairs. Check whether it is transitive
-
Find the value of \(cot(\frac{-15\pi}{4})\).
-
How many three digit odd numbers can be formed by using the digits 4, 5, 6, 7, 8, 9 if
(i) repetition of digit is not allowed,
(ii) repetition is allowed. -
Find the sum of first n terms of the series 12 + 32 + 52+...
-
If the equation 12x2 - 10xy + 2y2 + 14x - 5y + k = 0 represents a pair of straight lines, find k, find separate equation and also angle between them.
-
Let \(\vec a\) and \(\vec b\) be the position vectors of the points A and B. Prove that the position vectors of the points which trisects the line segment AB are \(\frac{\vec{a}+2 \vec{b}}{3} \text { and } \frac{\vec{b}+2 \vec{a}}{3} \text {. }\)
-
Discuss the continuity at x = 0 for \(f\left( x \right) =\begin{cases} \frac { 1-\cos { x } }{ { x }^{ 2 } } ,\quad x\neq 0 \\ \frac { 1 }{ 2 } ,\quad \quad \quad x=0 \end{cases}\)
-
Differentiate the following: y = sin(ex)
-
Evaluate : \(\int \sqrt{1+\cos 2 x} d x\)
-
A die is tossed thrice. find the probability of getting an odd number atleast once?
-
The owner of a small restaurant can prepare a particular meal at a cost of Rupee 100. He estimate that if the menu price of the meal is x rupees, then the number of customers who will order that meal at that price in an evening is given by the function D(x) = 200 - x. Express his day revenue total cost and profit on this meal as a function of x.
-
Resolve into partial fractions: \({{x^3+1}\over{x(x+1)^2}}\)
-
Solve sin x - 3 sin 2x+ sin 3x = cos x - 3 cos 2x + cos 3x.
-
Show that the sequence where log a,\(log\frac { { a }^{ 2 } }{ b^{ 1 } } log\frac { { a }^{ 2 } }{ { b }^{ 2 } } \) ..is an A.P
-
Find the equations of lines parallel to 3x - 4y- 5 = 0 at a unit distance from it.
-
If A =\(\begin{bmatrix} 1 &0 &2 \\0 & 2 & 1 \\2 &0 &3 \end{bmatrix}\) and A3 - 6A2 + 7A + KI = O, find the value of k.
-
Evaluate the following limits :\(lim_{x\rightarrow 0}{1-cosx\over x^2}\)
-
Show that\(f\left( x \right) ={ x }^{ 2 }\) is differentiable at x = 1 and find \(f^{ ' }\left( 1 \right) \)
-
Integrate the following with respect to x : \({8\over \sqrt{1-(4x)^2}}+{27\over \sqrt{1-9x^2}}-{15\over 1+25x^2}\)
-
Let the matrix M = \(\left[ \begin{matrix} x & y \\ z & 1 \end{matrix} \right] \), If x,y and z are chosen at random from the set {1, 2,3, } and repetition is allowed (i.e., x = y = z ), what is the probability that the given matrix M is a singular matrix?
-
Let A = {a, b, c}, What is the equivalence relation of smallest cardinality on A? What is the equivalence relation of largest cardinality on A?
-
Prove that \(\sqrt { 5 } \) is an irrational number
-
If \(\frac { cos^{ 4 }\alpha }{ { cos }^{ 2 }\beta } +\frac { { sin }^{ 4 }\alpha }{ { sin }^{ 2 }\beta } =1\) prove that \({ sin }^{ 4 }\alpha +{ sin }^{ 4 }\beta =2{ sin }^{ 2 }\alpha { sin }^{ 2 }\beta\)
-
How many three-digit numbers are there with 3 in the unit place?
(i) with repetition
(ii) without repetition. -
In a certain town, a viral disease caused severe health hazards upon its people disturbing their normal life. It was found that on each day, the virus which caused the disease spread in Geometric Progression. The amount of infectious virus particle gets doubled each day, being 5 particles on the first day. Find the day when the infectious virus particles just grow over 1,50,000 units?
-
Find the distance between the parallel lines
12x + 5y = 7 and 12x + 5y + 7 = 0. -
Show that the locus of the mid-point of the segment intercepted between the axes of the variable line x cos \(\alpha\) + y sin \(\alpha\) = p is \(\frac{1}{x^2}+\frac{1}{y^2}=\frac{4}{p^2}\) where p is a constant.
-
Determine the roots of the equation \(\begin{vmatrix} 1 &4 &2 0 \\ 1 & -2 & 5 \\ 1 &2x &5x^2 \end{vmatrix}=0\)
-
Let \(\overrightarrow { a } ,\overrightarrow { b } \) and \(\overrightarrow { c } \) be unit vectors such that \(\overrightarrow { a } \) is perpendicular to both \(\overrightarrow { b } \) and \(\overrightarrow { c } \) and further the angle between \(\overrightarrow { b } \) and \(\overrightarrow { c } \) is \(\frac { \pi }{ 6 } \). Then \(\overrightarrow { a } =\pm 2\left( \overrightarrow { b } \times \overrightarrow { c } \right) \)
-
The function \(f(x)={x^2-1\over x^3-1}\) is not defined at x = 1. What value must we give f(1) inorder to make f(x) continuous at x = 1?
-
Differentiate xx with respect to x log x
-
Integrate the following with respect to x : \(\frac{1}{3} \cos \left(\frac{x}{3}-4\right)+\frac{7}{7 x+9}+e^{\frac{x}{5}+3}\)
-
Evaluate \(\int { \frac { { x }^{ 2 }{ tan }^{ -1 }\left( { x }^{ 3 } \right) }{ 1+{ x }^{ 6 } } } \)dx
-
Two integers are selected at random from integers 1 to 11. If the sum is even, find the probability that both the numbers are odd.
20 x 1 = 20
7 x 2 = 14
7 x 3 = 21
7 x 5 = 35
*****************************************
11th Standard Maths Videos
TN 9th Maths Mensuration Important 2 Marks Questions With Answers Book Back and Creative
TN Class 9th Maths Mensuration Study Materials TN State Board / Matriculation 9th Maths Subject - Mensuration Two Mark Question and Answers






 11th Standard Maths Syllabus
11th Standard Maths Syllabus  11th Standard Maths Study Materials
11th Standard Maths Study Materials 11th Standard Maths MCQ Practise Tests
11th Standard Maths MCQ Practise Tests 

Reviews & Comments about 11th Standard Maths Public Exam Official Model Question Paper 2019
Write your Comment