Suppose X is the number of tails occurred when three fair coins are tossed once simultaneously. Find the values of the random variable X and number of points in its reverse images.

An urn contains 5 mangoes and 4 apples. Three fruits are taken at randaom. If the number of apples taken is a random variable, then find the values of the random variable and number of points in its inverse images.

A six sided die is marked '1' on one face, '3' on two of its faces, and '5' on remaining three faces. The die is thrown twice. If X denotes the total score in two throws, find
(i) the probability mass function
(ii) the cumulative distribution function
(iii) P(4 ≤ X < 10)
(iv) P(X ≥ 6)

The cumulative distribution function of a discrete random variable is given by

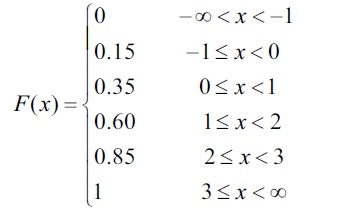
Find
(i) the probability mass function
(ii) P(X < 1 ) and
(iii) P(X \(\geq\)2)

A random variable X has the following probability mass function.

x	1	2	3	4	5
f(x)	k2	2k2	3k2	2k	3k

Find
(i) the value of k
(ii) P(2 \(\le\) X < 5)
(iii) P(3 < X )

The probability density function of X is given by \(f(x)=\begin{cases} \begin{matrix} kxe^{ -2x } & forx>0 \end{matrix} \\ \begin{matrix} 0 & for\quad x\le 0 \end{matrix} \end{cases}\) Find the value of k.

For the random variable X with the given probability mass function as below, find the mean and variance 

If the probability that a fluorescent light has a useful life of at least 600 hours is 0.9, find the probabilities that among 12 such lights
(i) exactly 10 will have a useful life of at least 600 hours;
(ii) at least 11 will have a useful life of at I least 600 hours;  
(iii) at least 2 will not have a useful life of at : least 600 hours.

Compute P(X = k) for the binomial distribution, B(n, p) where
n = 6, \(p=\frac { 1 }{ 3 } \), k = 3

Compute P(X = k) for the binomial distribution, B(n, p) where
\(P(X=10)=\left( \begin{matrix} 10 \\ 4 \end{matrix} \right) \left( \cfrac { 1 }{ 5 } \right) ^{ 4 }\left( 1-\cfrac { 1 }{ 5 } \right) ^{ 10-4 }\)

Compute P(X = k) for the binomial distribution, B(n, p) where
n = 9, \(p=\frac { 1 }{ 2 } \), k = 7

Using binomial distribution find the mean and variance of X for the following experiments
(i) A fair coin is tossed 100 times, and X denote the number of heads.
(ii) A fair die is tossed 240 times, and X denote the number of times that four appeared.

The probability that a certain kind of component will survive a electrical test is \(\frac { 3 }{ 4 } \). Find the probability that exactly 3 of the 5 components tested survive.

Suppose two coins are tossed once. If X denotes the number of tails,
(i) write down the sample space
(ii) find the inverse image of 1
(iii) the values of the random variable and number of elements in its inverse images

Find the binomial distribution function for each of the following.
(i) Five fair coins are tossed once and X denotes the number of heads.
(ii) A fair die is rolled 10 times and X denotes the number of times 4 appeared.