Find the rank of the matrix A = \(\left( \begin{matrix} 1 & 1 & 1 \\ 3 & 4 & 5 \\ 2 & 3 & 4 \end{matrix}\begin{matrix} 1 \\ 2 \\ 0 \end{matrix} \right) \) 

Find the rank of each of the following matrices.
\(\left( \begin{matrix} 3 & 1 & -5 \\ 1 & -2 & 1 \\ 1 & 5 & -7 \end{matrix}\begin{matrix} -1 \\ -5 \\ 2 \end{matrix} \right) \)

If \(\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{matrix} \right] \left[ \begin{matrix} x \\ y \\ z \end{matrix} \right] =\left[ \begin{matrix} 2 \\ -1 \\ 3 \end{matrix} \right] \) find x,y and z

Solve: 2x + 3y = 5, 6x + 5y = 11

Evaluate \(\int { { e }^{ x }\left( { x }^{ 2 }+2x \right) dx } \)

Integrate the following with respect to x
\(\frac { { e }^{ x } }{ { e }^{ 2x }-9 } \)

Evaluate \(\int { \frac { cos2x-cos2\alpha }{ cosx-cos\alpha } } dx\)

Evaluate \(\int { \frac { { ({ a }^{ x }{ +b }^{ x }) }^{ 2 } }{ { a }^{ x }b^{ x } } dx } \)

The marginal cost function of manufacturing x shoes is 6 +10x − 6x². The cost producing a pair of shoes is Rs. 12. Find the total and average cost function.

Calculate consumer’s surplus if the demand function p = 122 − 5x − 2x² and x = 6

Determine the cost of producing 3000 units of commodity if the marginal cost in rupees per unit is C'(x) = \(\frac{x}{3000}+2.50\)

The marginal revenue function is given by \(R'(x)=\frac { 3 }{ { x }^{ 2 } } -\frac { 2 }{ x } \). Find the revenue function and demand function if R(1) = 6

Solve : (D²−4D−1)y = e^−3x

Find the order and degree of the following differential equations.
\(\frac{d^{3} y}{d x^{3}}+3\left(\frac{d y}{d x}\right)^{3}+2 \frac{d y}{d x}=0\)

Solve: (x²-yx²)dy + (y²+xy²)dx = 0

Solve: (D²+1)y = 0 when x = 0, y = 2 and when x = \(\frac { \pi }{ 2 } \), y = -2.

Using graphic method, find the value of y when x = 38 from the following data:

x	10	20	30	40	50	60
y	63	55	44	34	29	22

Using graphic method, find the value of y when x = 48 from the following data:

x	40	50	60	70
y	6.2	7.2	9.1	12

Using graphic method, find the value of y when x=27.

x	10	15	20	25	30
y	35	32	29	26	23

Find the number of men getting wages between Rs. 30 and Rs. 35 from the following table.

Wages (x)	20 - 30	30 - 40	40 - 50	50 - 60
No. of men (y)	9	30	35	42

The number of miles an automobile tire lasts before it reaches a critical point in tread wear can be represented by a p.d.f.
\(f(x)= \begin{cases}\frac{1}{30} e^{-\frac{x}{30}}, & \text { for } x>0 \\ 0, & \text { for } x \leq 0\end{cases}\)
Find the expected number of miles (in thousands) a tire would last until it reaches the critical tread wear point.

The probability distribution function of a discrete random variable X is
\(F(x)=\left\{\begin{array}{l} 2k, x = 1 \\ 3k, x = 3 \\ 4k, x = 5 \\ 0, \text{otherwise} \end{array}\right.\)
where k is some constant. Find (a) k and (b) P(X>2).

If a random variable. X has the probability distribution

X	0	1	2	3	4	5
P(X=x)	a	2a	3a	4a	5a	6a

then find F(4)

Let X denote the number of hours you study during a randomly selected school day. The probability distribution function is
\(P(X=x)=\begin{cases} \begin{matrix} 0.1 & if\quad x=0 \end{matrix} \\ \begin{matrix} kx & if\quad x=1\quad or\quad 2 \end{matrix} \\ \begin{matrix} k(5-x) & if\quad x=3\quad or\quad 4 \end{matrix} \\ \begin{matrix} 0, & otherwise \end{matrix} \end{cases}\)
Find the value of k and what is the probability that you study atleast 2 hours.

The mean of Binomials distribution is 20 and standard deviation is 4. Find the parameters of the distribution.

If the chance of running a bus service according to schedule is 0.8, calculate the probability on a day schedule with 10 services :
(i) exactly one is late
(ii) atleast one is late

Find the value of K if X is a normal variate whose p.d.f is given by f(x)  = \(\frac { 1 }{ K } \)e^8x-4x2, -∞

The life of army shoes is normally distributed with mean 8 months and standard deviation 2 months. If 5000 pairs are issued, how many pairs would be expected to need replacement within 12 months.

The standard deviation of a sample of size 50 is 6.3. Determine the standard error whose population standard deviation is 6?

A sample of 100 items, draw from a universe with mean value 4 and S.D 3, has a mean value 63.5. Is the difference in the mean significant at 0.05 level of significance?

A random sample of marks in mathematics secured by 50 students out of 200 students showed a mean of 75 and a standard deviation of 10. Find the 95% confidence limits for the estimate of their mean marks.

The mean life time of 50 electric bulbs produced by a manufacturing company is estimated to be 825 hours with the S.D. of 110 hours. If II is the mean life time of all the bulbs produced by the company, test the hypothesis that μ = 900 hours at 5% level of significance.

Write a brief note on seasonal variations

Explain the method of fitting a straight line.

Fit a straight line trend for the following data using the method of least squares.

x	0	1	2	3	4
y	1	1	3	4	6

Calculate the seasonal indices for the following data by the method of simple average.

Year	Quarters
	I	II	III	IV
1994	78	66	84	80
1995	76	74	82	78
1996	72	68	80	70
1997	74	70	84	74
1998	76	74	86	82

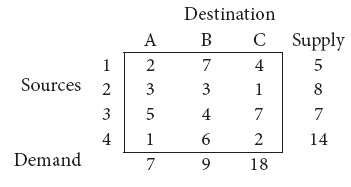
Obtain the initial solution for the following problem

A farmer wants to decide which of the three crops he should plant on his 100-acre farm. The profit from each is dependent on the rainfall during the growing season. The farmer has categorized the amount of rainfall as high medium and low. His estimated profit for each is shown in the table.

Rainfall	Estimated Conditional Profit(Rs.)
	crop A	crop B	crop C
High	8000	3500	5000
Medium	4500	4500	5000
Low	2000	5000	4000

If the farmer wishes to plant only crop, decide which should be his best crop using
(i) Maximin
(ii) Minimax

Find the initial basic feasible solution for the following transportation problem by Vogel's approximation method.

Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the operators I, II, III and IV.