- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Physics
-

Chemistry
-

Maths
-

Accountancy
-

Introductory Micro and Macroeconomics
-

Business Studies
-

Economics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Tamil
-

Bio Technology
-

Engineering Graphics
-

Entrepreneurship
-

Hindi Core
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Political Science
-

Psychology
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Mathematics
-

Chemistry
-

Biology
-

Physics
-

Business Studies
-

Accountancy
-

Economics
-

Computer Science
-

Bio Technology
-

English
-

Enterprenership
-

Geography
-

Hindi
-

History
-

Home Science
-

Physical Education
-

Political Science
-

Psychology
-

Sociology
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Mathematics
-

Social Science
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Science
-

Social Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students

12th Standard Business Maths English Medium Model 5 Mark Book Back Questions (New Syllabus 2020) Question Bank Software Sep-30 , 2020
12th Standard Business Maths English Medium Model 5 Mark Book Back Questions (New Syllabus 2020)
Model 5 Mark Book Back Questions (New Syllabus 2020)
12th Standard
-
Reg.No. :
Business Maths
Time :
01:00:00 Hrs
Total Marks :
195
-
Find k, if the equations x + y + z = 7, x + 2y + 3z = 18, y + kz = 6 are inconsistent
-
A total of Rs. 8,500 was invested in three interest earning accounts. The interest rates were 2%, 3% and 6% if the total simple interest for one year was Rs. 380 and the amount, invested at 6% was equal to the sum of the amounts in the other two accounts, then how much was invested in each account? (use Cramer’s rule).
-
Find k if the equations x + y + z = 1, 3x − y − z = 4, x+ 5y + 5z = k are inconsistent.
-
Integrate the following with respect to x.
\(\frac { { 3x }^{ 2 }-2x+5 }{ { \left( x-1 \right) }\left( x^{ 2 }+5 \right) } \) -
Evaluate \(\int _{ 1 }^{ e }{ \log x } \) dx
-
Evaluate the following integrals as the limit of the sum:
\(\int _{ 1 }^{ 3 }{ xdx } \) -
Using integration find the area of the circle whose center is at the origin and the radius is a units.
-
The price of a machine is Rs. 5,00,000 with an estimated life of 12 years. The estimated salvage value is Rs. 30,000. The machine can be rented at Rs. 72,000 per year. The present value of the rental payment is calculated at 9% interest rate. Find out whether it is advisable to rent the machine.(e−1.08 = 0.3396).
-
The marginal cost of production of a firm is given by C'(x) = 5 + 0.13x, the marginal revenue is given by R'(x) = 18 and the fixed cost is Rs. 120. Find the profit function.
-
The demand equation for a product is pd = 20 − 5x and the supply equation is ps = 4x + 8. Determine the consumer’s surplus and producer’s surplus under market equilibrium.
-
The normal lines to a given curve at each point(x,y) on the curve pass through the point (1, 0). The curve passes through the point (1, 2). Formulate the differential equation representing the problem and hence find the equation of the curve.
-
Solve the following homogeneous differential equations.
\((x-y)\frac { dy }{ dx } =x+3y\). -
Solve \(\frac { dy }{ dx } \) −3ycot x = sin 2x given that y = 2 when x = \(\frac { \pi }{ 2 } \)
-
\(\frac { dy }{ dx } +\frac { y }{ x } ={ xe }^{ x }\)
-
Solve the following differential equations (3D2 + D − 14)y = 13e2x
-
Solve \(\frac { dy }{ dx } +ycosx+x=2cosx\).
-
The population of a certain town is as follows
Year : x 1941 1951 1961 1971 1981 1991 Population in lakhs:y 20 24 29 36 46 51 Using appropriate interpolation formula, estimate the population during the period 1946.
-
Find the missing entries from the following
x 0 1 2 3 4 5 y = f(x) 0 - 8 15 - 35 -
Find f(2.8) from the following table.
x 0 1 2 3 f(x) 1 2 11 34 -
Using Lagrange’s interpolation formula find a polynomial which passes through the points (0, –12), (1, 0), (3, 6) and (4,12).
-
A continuous random variable X has p.d.f
f(x) = 5x4, 0\(\le\)x\(\le\)1
Find a1 and a2 such that
i) P[X\(\le\)a1] = P[X>a1]
ii) P[X>a2] = 0.05 -
A continuous random variable X has the following distribution function:
\(f(x)=\left\{\begin{array}{l} 0 , \text{if} \ x \leq1 \\ k(x-1)^4, \text{if} \ 1< x \leq 3 \\ 1, \text{if} \ x > 3 \end{array}\right.\)
Find (i) k and (ii) the probability density function. -
Determine the mean and variance of a discrete random variable, given its distribution as follows.
X = x 1 2 3 4 5 6 Fx(x) \(\frac{1}{6}\) \(\frac{2}{6}\) \(\frac{3}{6}\) \(\frac{4}{6}\) \(\frac{5}{6}\) 1 -
The probability function of a random variable X is given by
\(p(x)=\left\{\begin{array}{l} \frac{1}{4}, \text { for } x=-2 \\ \frac{1}{4}, \text { for } x=0 \\ \frac{1}{2}, \text { for } x=10 \\ 0, \text { elsewhere } \end{array}\right.\)
Evaluate the following probabilities.
P(X<0) -
If the probability that an individual suffers a bad reaction from injection of a given serum is 0.001, determines the probability that out of 2,000 individuals
(a) exactly 3, and
(b) more than 2 individuals will suffer a bad reaction. -
If 5% of the items produced turn out to be defective, then find out the probability that out of 20 items selected at random there are
(i) exactly three defectives
(ii) atleast two defectives
(iii) exactly 4 defectives
(iv) find the mean and variance -
The average number of customers, who appear in a counter of a certain bank per minute is two. Find the probability that during a given minute
(i) No customer appears
(ii) three or more customers appear -
A manufacturer of metal pistons finds that on the average, 12% of his pistons are rejected because they are either oversize or undersize. What is the probability that a batch of 10 pistons will contain
(a) no more than 2 rejects?
(b) at least 2 rejects? -
A machine produces a component of a product with a standard deviation of 1.6 cm in length. A random sample of 64 componentsvwas selected from the output and this sample has a mean length of 90 cm. The customer will reject the part if it is either less than 88 cm or more than 92 cm. Does the 95% confidence interval for the true mean length of all the components produced ensure acceptance by the customer?
-
A random sample of 60 observations was drawn from a large population and its standard deviation was found to be 2.5. Calculate the suitable standard error that this sample is taken from a population with standard deviation 3?
-
Given below are the data relating to the sales of a product in a district.
Fit a straight line trend by the method of least squares and tabulate the trend values.Year 1995 1996 1997 1998 1999 2000 2001 2002 Sales 6.7 5.3 4.3 6.1 5.6 7.9 5.8 6.1 -
Calculate Fisher’s price index number and show that it satisfies both Time Reversal Test and Factor Reversal Test for data given below.
Commodities Price Quandity 2003 2009 2003 2009 Rice 10 13 4 6 Wheat 125 18 7 8 Rent 25 29 5 9 Fuel 11 14 8 10 Miscellaneous 14 17 6 7 -
Calculate the cost of living index number by consumer price index number for the year 2016 with respect to base year 2011 of the following data
\(\begin{array}{|c|c|c|c|} \hline & {\text { Price }} & \\ \begin{array}{c} \text { Commodities } \\ \text { } \end{array} & \begin{array}{c} \text { Base } \\ \text { year } \end{array} & \begin{array}{c} \text { Current } \\ \text { year } \end{array} & \text { Quantity } \\ \hline \text { Rice } & 32 & 48 & 25 \\ \hline \text { Sugar } & 25 & 42 & 10 \\ \hline \text { Oil } & 54 & 85 & 6 \\ \hline \text { Coffee } & 250 & 460 & 1 \\ \hline \text { Tea } & 175 & 275 & 2 \\ \hline \end{array}\) -
The sales of a commodity in tones varied from January 2010 to December 2010 as follows:
In year 2010 Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec Sales (in tones) 280 240 270 300 280 290 210 200 230 200 230 210 Fit a trend line by the method of semi-average.
-
Using Fisher’s Ideal Formula, compute price index number for 1999 with 1996 as base year, given the following:
Year Commodity: A Commodity: B Commodity: C Price (Rs.) Quantity (Kg) Price (Rs.) Quantity (Kg) Price (Rs.) Quantity (Kg) 1996 5 10 8 6 6 3 1999 4 12 7 7 5 4 -
A quality control inspector has taken ten samples of size four packets each from a potato chips company. The contents of the sample are given below, Calculate the control limits for mean and range chart.
Sample Number Observations 1 2 3 4 1 12.5 12.3 12.6 12.7 2 12.8 12.4 12.4 12.8 3 12.1 12.6 12.5 12.4 4 12.2 12.6 12.5 12.3 5 12.4 12.5 12.5 12.5 6 12.3 12.4 12.6 12.6 7 12.6 12.7 12.5 12.8 8 12.4 12.3 12.6 12.5 9 12.6 12.5 12.3 12.6 10 12.1 12.7 12.5 12.8 (Given for n = 5, A2 = 0.58, D3 = 0 and D4 = 2.115)
-
Using the following data, construct Fisher’s Ideal Index Number and Show that it satisfies Factor Reversal Test and Time Reversal Test?
Commodities Price Quantity Base Year Current year Base Year Current year Wheat 6 10 50 56 Ghee 2 2 100 120 Firewood 4 6 60 60 Sugar 10 12 30 24 Cloth 8 12 40 36 -
Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.
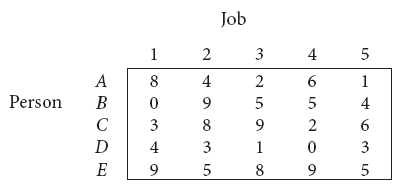
-
Determine an initial basic feasible solution to the following transportation problem by using North West Corner rule
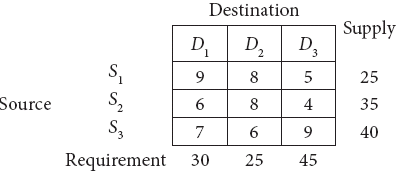
Part A
39 x 5 = 195
*****************************************
12th Standard Business Maths and Statistics Videos
TN 12th Business Maths Applications of Matrices and Determinants 50 Important 1 Marks Questions With
TN Class 12th 2024 Business Maths and Statistics Applications of Matrices and Determinants Study Materials TN State Board / Matriculation 12th Business Maths and Statistics Subject - Applications of Matrices and Determinants One Mark Question and Answers






 12th Standard Business Maths and Statistics Syllabus
12th Standard Business Maths and Statistics Syllabus  12th Standard Business Maths and Statistics Study Materials
12th Standard Business Maths and Statistics Study Materials 12th Standard Business Maths and Statistics MCQ Practise Tests
12th Standard Business Maths and Statistics MCQ Practise Tests 

Reviews & Comments about 12th Standard Business Maths English Medium Model 5 Mark Book Back Questions (New Syllabus 2020)
Write your Comment