Find the rank of the matrix A = \(\left( \begin{matrix} 1 & 1 & 1 \\ 3 & 4 & 5 \\ 2 & 3 & 4 \end{matrix}\begin{matrix} 1 \\ 2 \\ 0 \end{matrix} \right) \) 

A total of Rs. 8,600 was invested in two accounts. One account earned \(4\frac { 3 }{ 4 } %\)% annual interest and the other earned \(6\frac { 1 }{ 2 } %\)% annual interest. If the total interest for one year was Rs. 431.25, how much was invested in each account? (Use determinant method).

Find the rank of the matrix A =\(\left( \begin{matrix} 4 & 5 & 2 \\ 3 & 2 & 1 \\ 4 & 4 & 8 \end{matrix}\begin{matrix} 2 \\ 6 \\ 0 \end{matrix} \right) \)

Evaluate \(\int { \frac { { 2x }^{ 2 }-14x+24 }{ x-3 } dx } \)

Integrate the following with respect to x.
\(\frac { { e }^{ 3x }+{ e }^{ 5x } }{ { e }^{ x }+{ e }^{ -x } } \)

Integrate the following with respect to x.
x log x

Integrate the following with respect to x.
\(\frac { { x }^{ e-1 }+{ e }^{ x-1 } }{ { x }^{ e }+{ e }^{ x } } \)

Integrate the following with respect to x
\(\frac { 1 }{ { x }^{ 2 }-x-2 } \)

Evaluate \(\int _{ 0 }^{ 1 }{ [{ e }^{ a \log x }+{ e }^{ x \log a }] } dx\)

Evaluate the following: f(x) = \(\begin{cases} cx, \\ 0, \end{cases}\begin{matrix} 0 < x < 1 \\ \text{otherwise} \end{matrix}\)

Evaluate the following integrals:
ഽ(x +1)² log x dx

The marginal cost function MC = 2 + 5e^x Find C if C (0)=100

The marginal cost function of a product is given by \(\frac { dC }{ dx } \) = 100 −10x + 0.1x² where x is the output. Obtain the total and the average cost function of the firm under the assumption, that its fixed cost is Rs. 500.

The demand and supply functions under perfect competition are p_d = 1600 − x² and p_s = 2x² + 400 respectively. Find the producer’s surplus.

Find the differential equation of the family of curves y = e^x (acos x + bsin x) where a and b are arbitrary constants.

(D²−2D−15)y = 0 given that \(\frac{dy}{dx}\)= 0 and \(\frac{d^2 y}{dx^2}\) = 2 when x = 0

By constructing a difference table and using the second order differences as constant, find the sixth term of the series 8,12,19,29,42…

Using graphic method, find the value of y when x = 48 from the following data:

x	40	50	60	70
y	6.2	7.2	9.1	12

A continuous random variable X has the following p.d.f f(x) = ax, 0\(\le\)x\(\le\)1
Determine the constant a and also find P\(\\ \left[ X\le \frac { 1 }{ 2 } \right] \)

If f (x) is defined by f(x)=ke^-2x,  0\(\le\)x<\(\infty\) is a density function. Determine the constant k and also find mean.

A person tosses a coin and is to receive Rs. 4 for a head and is to pay Rs. 2 for a tail. Find the expectation and variance of his gains.

What is the probability of guessing correctly atleast six of the ten answers in a TRUE/FALSE objective test?

Consider five mice from the same litter, all suffering from Vitamin A deficiency. They are fed a certain dose of carrots. The positive reaction means recovery from the disease. Assume that the probability of recovery is 0.73. What is the probability that atleast 3 of the 5 mice recover.

The birth weight of babies is Normally distributed with mean 3,500 g and standard deviation 500 g. What is the probability that a baby is born that weighs less than 3,100 g?

A die is thrown 9000 times and a throw of 3 or 4 is observed 3240 times. Find the standard error of the proportion for an unbiased die. .

Fit a trend line by the method of semi-averages for the given data.

Year	2000	2001	2002	2003	2004	2005	2006
Production	105	115	120	100	110	125	135

Using three yearly moving averages, Determine the trend values from the following data.

Year	Profit	Year	Profit
2001	142	2007	241
2002	148	2008	263
2003	154	2009	280
2004	146	2010	302
2005	157	2011	326
2006	202	2012	353

Determine an initial basic feasible solution to the following transportation problem using North West corner rule.

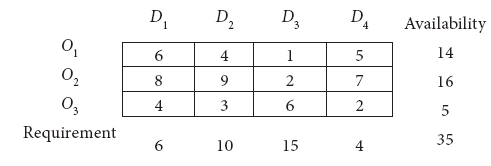
Here O_i and D_j represent i^th origin and j^th destination.

Solve the following assignment problem.

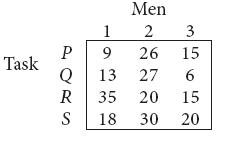
Consider the following pay-off matrix

Alternative	Pay – offs (Conditional events)
	A1	A2	A3	A4
E1	7	12	20	27
E2	10	9	10	25
E3	23	20	14	23
E4	32	24	21	17

Using minmax principle, determine the best alternative.

Determine basic feasible solution to the following transportation problem using North west Corner rule.

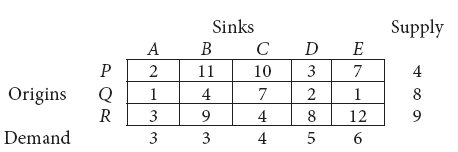
A farmer wants to decide which of the three crops he should plant on his 100-acre farm. The profit from each is dependent on the rainfall during the growing season. The farmer has categorized the amount of rainfall as high medium and low. His estimated profit for each is shown in the table.

Rainfall	Estimated Conditional Profit(Rs.)
	crop A	crop B	crop C
High	8000	3500	5000
Medium	4500	4500	5000
Low	2000	5000	4000

If the farmer wishes to plant only crop, decide which should be his best crop using
(i) Maximin
(ii) Minimax