If A is a non-singular matrix of odd order, prove that |adj A| is positive

Find the rank of each of the following matrices:
\(\left[ \begin{matrix} 3 & 2 & 5 \\ 1 & 1 & 2 \\ 3 & 3 & 6 \end{matrix} \right] \) 

If z₁ = 1 - 3i, z₂ = - 4i, and z₃ = 5 , show that (z₁ + z₂) + z₃ = z₁+ (z₂ + z₃)

Simplify \(\left( \frac { 1+i }{ 1-i } \right) ^{ 3 }-\left( \frac { 1-i }{ 1+i } \right) ^{ 3 }\) into rectangular form

Construct a cubic equation with roots 1, 2 and 3

Formulate into a mathematical problem to find a number such that when its cube root is added to it, the result is 6.

Find the principal value of sin^-1(2), if it exists.

Find all the values of x such that -10\(\pi\)\(\le x\le\)10\(\pi\) and sin x = 0 

Obtain the equation of the circles with radius 5 cm and touching x-axis at the origin in general form.

If y = 2\(\sqrt2\)x + c is a tangent to the circle x² + y² = 16, find the value of c.

Find the volume of the parallelepiped whose coterminous edges are represented by the vectors \(-6\hat { i } +14\hat { j } +10\hat { k } ,14\hat { i } -10\hat { j } -6\hat { k } \) and \(2\hat { i } +4\hat { j } -2\hat { k } \)

The volume of the parallelepiped whose coterminus edges are \(7\hat { i } +\lambda \hat { j } -3\hat { k } ,\hat { i } +2\hat { j } -\hat { k } \), \(-3\hat { i } +7\hat { j } +5\hat { k } \) is 90 cubic units. Find the value of λ.

Find the angle of intersection of the curve y = sin x with the positive x -axis.

A truck travels on a toll road with a speed limit of 80 km/hr. The truck completes a 164 km journey in 2 hours. At the end of the toll road the trucker is issued with a speed violation ticket. Justify this using the Mean Value Theorem.

The time T, taken for a complete oscillation of a single pendulum with length l, is given by the equation T = 2ㅠ\(\sqrt { \frac { 1 }{ g } } \), where g is a constant. Find the approximate percentage error in the calculated value of T corresponding to an error of 2 percent in the value of l.

Evaluate :\(\int _{ 0 }^{ 1 }{ [2x] } dx\) where [⋅] is the greatest integer function

Evaluate:  \(\int ^{\frac{\pi}{2}}_{\frac{\pi}{2}}\)x cos x dx.

Find the values of the following:
\(\int ^\frac{\pi}{2}_{0}\)sin ⁵x cos⁴xdx

For each of the following differential equations, determine its order, degree (if exists)
\({ \left( \frac { d^2y }{ dx^2 } \right) }^{ 3 }=\sqrt { 1+\left( \frac { dy }{ dx } \right) } \)

An urn contains 5 mangoes and 4 apples. Three fruits are taken at randaom. If the number of apples taken is a random variable, then find the values of the random variable and number of points in its inverse images.

The cumulative distribution function of a discrete random variable is given by

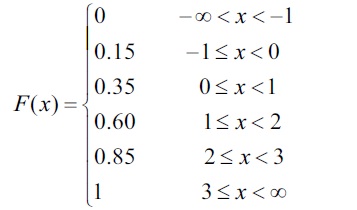
Find
(i) the probability mass function
(ii) P(X < 1 ) and
(iii) P(X \(\geq\)2)

For the random variable X with the given probability mass function as below, find the mean and variance 

Let A =\(\begin{bmatrix} 0 & 1 \\ 1 & 1 \end{bmatrix},B=\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix}\)be any two boolean matrices of the same type. Find AvB and A\(\wedge\)B.

Let p: Jupiter is a planet and q: India is an island be any two simple statements. Give verbal sentence describing each of the following statements.
(i) ¬p
(ii) p ∧ ¬q
(iii) ¬p ∨ q
(iv) p➝ ¬q
(v) p↔q