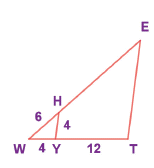
In the given figure YH||TE . Prove that ΔWHY～ΔWET and also find HE and TE.

In the given figure, ∠CIP ≡ ∠COP and ∠HIP ≡ ∠HOP . Prove that IP ≡ OP.

In the given figure, D is the midpoint of OE and ∠CDE = 90°. Prove that ΔODC ≡ ΔEDC

In the given figure, find PT given that l₁|| l₂.

In the figure, given that ∠1 = ∠2 and ∠3  ≡ ∠4. Prove that ΔMUG ≡ ΔTUB.

In the figure, ∠TEN ≡ ∠TON = 90^o and TO ≡ TE. Prove that ∠ORN ≡ ∠ERN.

In the figure, PQ ≡ TS, Q is midpoint of PR, S is the midpoint TR and ∠PQU ≡ ∠TSU. Prove that QU ≡ SU.

Construct the following quadrilaterals with the given measurements and also find their area.
KITE, KI = 5.4 cm, IT = 4.6 cm, TE = 4.5 cm, KE = 4.8 cm and IE = 6 cm.

Construct the following quadrilaterals with the given measurements and also find their area.
PLAY, PL = 7 cm, LA = 6 cm, AY = 6 cm, PA = 8 cm and LY = 7 cm.

Construct the following quadrilaterals with the given measurements and also find their area.
AGRI, AG = 4.5 cm, GR = 3.8 cm, ∠A = 60°, ∠G = 110° and ∠R = 90°.

Construct the following quadrilaterals with the given measurements and also find their area.
YOGA, YO = 6 cm, OG = 6 cm, ∠O = 55°, ∠G = 35° and ∠A = 100°.

Fill in the blanks with the correct term from the given list.
(in proportion, similar, corresponding, congruent shape, area, equal)
(i) Corresponding sides of similar triangles are _______.
(ii) Similar triangles have the same _________ but not necessarily the same size.
(iii) In similar triangles, ______ sides are opposite to equal angles.
(iv) The symbol ≡ is used to represent _______ triangles.
(v) The symbol ～ is used to represent ________ triangles

Is it possible to construct a quadrilateral PQRS with PQ = 5 cm, QR = 3 cm, RS = 6 cm, PS = 7 cm and PR = 10 cm. If not, why?

In the figure AB\(\bot \) BC and DE\(\bot \)AC prove that \(\triangle \)ABC ~\(\triangle \)AED.

In the given figure if \(\angle \)P =\(\angle \)RTS, prove that \(\triangle \)RPQ ~\(\triangle \) RTS.