If n(A \(\cup \) B \(\cup \) C) = 40, n(A) = 30, n(B) = 25, n(C) = 20, n(A\(\cap \)B) = 12, n(B\(\cap \)C) = 18 and n(A\(\cap \)C) = 15 , then n(A\(\cap \)B\(\cap \)C) is ___________

\(\left[ n\left( A\cup B\cup C \right) ^{ ' } \right] \)=_______

if \(\frac { 1 }{ 7 } \) = \(0.\overline { 142857 } \) then the value of \(\frac { 5 }{ 7 } \) ________.

\(\sqrt [ 4 ]{ 405 } =h\sqrt [ 4 ]{ 5 } \), then h = ____________

If x⁵¹ + 51 is divided by x + 1, then the remainder is _______.

If x - 2 is a factor of q(x), then the remainder is___________

The angle sum of a convex polygon with number of sides 7 is ________

Signs of the abscissa and ordinate of a point in the fourth quadrant are respectively

The point which is on y-axis with ordinate - 5 is _____________

The mean of the first 10 prime numbers is ___________

The mean of 5, 9, x, 17,and 21 is 13 then find the value of x ___________

The value of \(\frac { sin{ 29 }^{ 0 }31' }{ cos{ 60 }^{ 0 }29' } \) is

The number of bricks each measuring 50 cm × 30 cm × 20 cm that will be required to build a wall whose dimensions are 5 m × 3 m × 2 m is _______.

A random experiment contains

Write the set of letters of the following words in Roster form
ASSESSMENT

Express the following in the form  \({p\over q},\)  where p and q are integers and q \(\ne\) 0.
\(0.5\overline {7}\)

Find the value of \(\left( \frac { 1 }{ 27 } \right) ^{ \frac { -2 }{ 3 } }\)

We used to write \(\pi\) as \(\frac{22}{7}.\) Can we say \(\pi\) is a rational number?

Factorise the following: m³+\(\frac{1}{m^2}\)-23

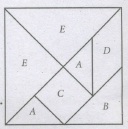
This is a copy of the tangram puzzle. The tangram puzzle consists of 7 geometric pieces which are normally boxed in the shape·of a square. The pieces, called 'tans', are used to create different patterns including animals, people, numbers, geometric shapes and many more.
You can make several polygons using the pieces in different ways.

Show that the line segment joining the mid-points of two sides of a triangle is half of the third side
(Hint: Place triangle ABC in a clever way such that A is (0, 0), B is (2a, 0) and C to be (2b, 2c). Now consider the line segment joining the mid-points of AC and BC. This will make calculations simpler).

If A (10, 11) and B (2 ,3) are the coordinates of end points of diameter of circle. Then find the centre of the circle.

A car travels, at an uniform speed. At 2 pm it is at a distance of 5 km at 6 pm it is at a distance of 120 km. Using section formula, find at what distance it will reach 2 midnight.

A set of numbers consists of five 4’s, four 5’s, nine 6’s,and six 9’s. What is the mode.

If 3 (tan \(\theta\)) + 4 (sec \(\theta\) \(\times\) sin 6) = 24. Then find all the trigonometric ratios of the angle \(\theta\)

Find the value of \(\cfrac { cos{ 63 }^{ 0 }20' }{ sin{ 26 }^{ 0 }40' } \)

Using Heron's formula, find the area of a triangle whose sides are 41 m, 15 m, 25 m.

1500 families were surveyed and following data was recorded about their maids at homes

A family is selected at random. Find the probability that the family selected has
(i) Both types of maids
(ii) Part time maids
(iii) No maids

Out of 500 car owners investigated, 400 owned car A and 200 owned car B, 50 owned both A and B cars. Is this data correct?

In a class there are 40 students. 26 have opted for Mathematics and 24 have opted for Science. How many student have opted for Mathematics and Science.

Express the following decimal expression into rational numbers \(0.\overline { 0001 } \)

Find the value of a and b if \(\frac { \sqrt { 7 } -2 }{ \sqrt { 7 } +2 } \) = a\(\sqrt{7}\) + b

Arrange in ascending order:\(\sqrt [ 3 ]{ 5 } ,\sqrt [ 4 ]{ 7 } ,\sqrt [ 2 ]{ 6 } \)

Find the GCD of (x - 7)², (x + 7)², (x - 4)³

Solve by cross-multiplication method
(i) 8x − 3y = 12 ; 5x = 2y + 7
(ii) 6x + 7y −11 = 0 ; 5x + 2y = 13
(iii) \(\frac { 2 }{ x } +\frac { 3 }{ y } =5;\frac { 3 }{ x } -\frac { 1 }{ y } +9=0\)

Construct the ΔPQR such that PQ = 5cm, PR= 6cm and ㄥQPP = 60° and locate its centroid.

The abscissa of a point A is equal to its ordinate, and its distance from the point B(1, 3) is 10 units, What are the coordinates of A?

The point (3, −4) is the centre of a circle. If AB is a diameter of the circle and B is (5, −6), find the coordinates of A.

The median of observation 11,12,14,18, x+12, x+4, 30, 32, 35, 41 arrenged in ascending order is 24. Find the values of x.

Evaluate:
(i) \(\frac { sin\ 49° }{ cos\ 41° } \) 
(ii) \(\frac { sec\ 63° }{ cosec\ 27° } \)

Two identical cubes of side 7 cm are joined end to end. Find the Total and Lateral surface area of the new resulting cuboid.

When a dice is rolled, find the probability to get the number greater than 4?