- State Board
-
12th Standard
-

Biology
-

Computer Applications
-

Computer Science
-

Business Maths and Statistics
-

Commerce
-

Economics
-

Maths
-

Chemistry
-

Physics
-

Computer Technology
-

History
-

Accountancy
-

Tamil
-

Maths
-

Chemistry
-

Physics
-

Biology
-

Computer Science
-

Business Maths and Statistics
-

Economics
-

Commerce
-

Accountancy
-

History
-

Computer Applications
-

Computer Technology
-

English
12th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
11th Standard
-

Maths
-

Biology
-

உயிரியல் - தாவரவியல்
-

Economics
-

Physics
-

Chemistry
-

History
-

Business Maths and Statistics
-

Computer Science
-

Accountancy
-

Commerce
-

Computer Applications
-

Computer Technology
-

Tamil
-

Maths
-

Commerce
-

Economics
-

Biology
-

Business Maths and Statistics
-

Accountancy
-

Computer Science
-

Physics
-

Chemistry
-

Computer Applications
-

History
-

Computer Technology
-

Tamil
-

English
11th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
9th Standard
-

-

-

-

-

-

-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
9th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
6th Standard
-

Maths
-

Science
-

Social Science
-

Maths
-

Science
-

Social Science
6th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
10th Standard
-

Maths
-

Science
-

Social Science
-

Tamil
-

Maths
-

Science
-

Social Science
-

English
-

English
10th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
7th Standard
-

Maths
-

Science
-

Maths
-

Science
-

Social Science
7th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
8th Standard
-

கணிதம் - old
-

Science
-

Social Science
-

கணிதம்
-

Maths
-

Science
-

Social Science
8th Standard stateboard question papers & Study material
தமிழ் Subjects
English Subjects
-
-
12th Standard
- CBSE Board
-
12th Standard CBSE
-

Biology
-

Physics
-

Chemistry
-

Maths
-

Accountancy
-

Introductory Micro and Macroeconomics
-

Business Studies
-

Economics
-

Computer Science
-

Geography
-

English
-

History
-

Indian Society
-

Physical Education
-

Sociology
-

Tamil
-

Bio Technology
-

Engineering Graphics
-

Entrepreneurship
-

Hindi Core
-

Hindi Elective
-

Home Science
-

Legal Studies
-

Political Science
-

Psychology
12th Standard CBSE Subject Question Paper & Study Material
-
-
11th Standard CBSE
-

Mathematics
-

Chemistry
-

Biology
-

Physics
-

Business Studies
-

Accountancy
-

Economics
-

Computer Science
-

Bio Technology
-

English
-

Enterprenership
-

Geography
-

Hindi
-

History
-

Home Science
-

Physical Education
-

Political Science
-

Psychology
-

Sociology
-

Applied Mathematics
11th Standard CBSE Subject Question Paper & Study Material
-
- 10th Standard CBSE
-
9th Standard CBSE
-

Mathematics
-

Social Science
-

Science
-

English
-

Hindi
9th Standard CBSE Subject Question Paper & Study Material
-
-
8th Standard CBSE
-

Science
-

Social Science
-

Mathematics
-

English
8th Standard CBSE Subject Question Paper & Study Material
-
-
7th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
7th Standard CBSE Subject Question Paper & Study Material
-
-
6th Standard CBSE
-

Mathematics
-

Science
-

Social Science
-

English
6th Standard CBSE Subject Question Paper & Study Material
-
-
12th Standard CBSE
- Free Online Test
- News
- Study Materials
-
Students
-

Stateboard Tamil Nadu
-

CBSE Board
-

Free Online Tests
-

Educational News
-

Scholarships
-

Entrance Exams India
-

Video Materials
Study Materials , News and Scholarships
-
-
Students

9th Standard Maths Annual Exam Model Question Paper III - 2019 - 2020 Question Bank Software Feb-06 , 2020
9th Standard Maths Annual Exam Model Question Paper III - 2019 - 2020
Annual Exam Model Question Paper 2019 - 2020 Part-V
9th Standard
-
Reg.No. :
Maths
Time :
02:45:00 Hrs
Total Marks :
100
-
If U = {x | x ∈ N, x < 10} and A = {x | x ∈ N, 2 ≤ x < 6} then (A′)′ is –––––––––.
(a){1, 6, 7, 8, 9}
(b){1, 2, 3, 4}
(c){2, 3, 4, 5}
(d){ }
-
The set (A - B) U(B - A) is ___________
(a)AΔB
(b)AUB
(c)A∩B
(d)A'UB'
-
The length and breadth of a rectangular plot are 5 \(\times\) 105 and 4 \(\times\) 104 metres respectively. Its area is ______.
(a)9 \(\times\) 101 m2
(b)9 \(\times\) 109 m2
(c)2 \(\times\) 1010 m2
(d)20 \(\times\) 1020 m2
-
Rationalising the denominator \(\cfrac { 1 }{ \sqrt [ 3 ]{ 3 } } \) ___________
(a)3
(b)\(\cfrac { { 3 }^{ \frac { 2 }{ 3 } } }{ 3 } \)
(c)\(\sqrt { 3 } \)
(d)\(\sqrt [ 3 ]{ 3 } \)
-
The value of the polynomial f(x) = 6x - 3x2+9 when x = -1 is _____________________
(a)0
(b)1
(c)2
(d)3
-
The linear equation in one variable is __________
(a)2x + 2 = y
(b)5x − 7 = 6 − 2x
(c)2t(5 − t) = 0
(d)7p − q = 0
-
The perpendicular line from the centre of the circle to the chord divided the chord in the ratio________
(a)1: 1
(b)1: 2
(c)2: 1
(d)1: 3
-
The distance between the points (4, -1) and the origin is___________
(a)\(\sqrt{24}\)
(b)\(\sqrt{37}\)
(c)\(\sqrt{26}\)
(d)\(\sqrt{17}\)
-
In what ratio does the y-axis divides the line joining the points (−5, 1) and (2, 3) internally ______.
(a)1 :3
(b)2 :5
(c)3 :1
(d)5 :2
-
A particular observation which occurs maximum number of times in a given data is called its _______.
(a)Frequency
(b)range
(c)mode
(d)Median
-
The mean of 5, 9, x, 17,and 21 is 13 then find the value of x ___________
(a)9
(b)13
(c)17
(d)21
-
The value of 2tan30° tan60° is
(a)1
(b)2
(c)\(2\sqrt { 3 } \)
(d)6
-
The perimeter of an equilateral triangle is 30 cm. The area is _______.
(a)\(10\sqrt { 3 } \) cm2
(b)\(12\sqrt { 3 } \) cm2
(c)\(15\sqrt { 3 } \) cm2
(d)\(25\sqrt { 3 } \) cm 2
-
A number between 0 and 1 that is used to measure uncertainty is called _______.
(a)Random variable
(b)Trial
(c)Simple event
(d)Probability
-
If U = {a, b, c, d, e, f, g, h}, A = {b, d, f, h} and B = {a, d, e, h}, find the following sets. A′\(\cup \) B′
-
Without actual division classify the decimal expansion of the following numbers as terminating or non-terminating and recurring.
\(7\over 16\) -
Write the following in the form of 5n
\(\sqrt{5}\) -
The mass of the Earth is 5.97 \(\times\) 1024 kg and that of the Moon is 0.073 \(\times\) 1024 kg. What is their total mass?
-
Factorise the following expressions: pr+qr+pq+p2
-
Which ones are not quadrilaterals?

-
Find the distance between the following pairs of points. (3,4) and (– 7, 2)
-
If A (10, 11) and B (2 ,3) are the coordinates of end points of diameter of circle. Then find the centre of the circle.
-
Find the coordinates of the point which divides, the line segment joining the point A (3,7) and B (-11, -2) in the ratio 5 : 1.
-
A set of numbers consists of five 4’s, four 5’s, nine 6’s,and six 9’s. What is the mode.
-
Find the six trigo'nometric ratios of the angle 0 using the diagram
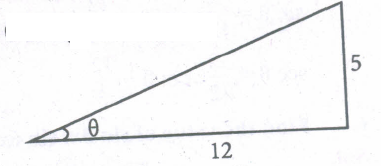
-
Find the value of sin 3x. sin 6x. sin 9x when x = 10°
-
Find the volume of a cube whose surface are is a 96 cm2.
-
A manufacturer tested 7000 LED lights at random and found that 25 of them were defective. If a LED light is selected at random, what is the probability that the selected LED light is a defective one.
-
Given that A = {1,3,5,7} B = {1,2,4,6,8}. Find
(i) AΔB and
(ii) BΔA -
If K = {a,b,d e f } L = {b,c,d,g} and M = {a,b,c,d,h}, then find the following:
(i) K \(\cup \)(L \(\cap \) M)
(ii) K \(\cap \)(L \(\cup \) M)
(iii) (K\(\cup \)L)\(\cap \)(K\(\cup \)M)
(iv) (K\(\cap \)L)\(\cup \)(K\(\cap \)M) -
Express the following decimal expression into rational numbers. \(2.\overline { 327 } \)
-
(i) Add 3\(\sqrt{7}\) and 5\(\sqrt{7}\) . Check whether the sum is rational or irrational.
(ii) Subtract 4\(\sqrt{5}\) from 7\(\sqrt{5}\) . Is the answer rational or irrational? -
Write in scientific notation ;(60000000)3
-
Find quotient and the remainder when f(x) is divided by g(x) x4 – 3x3 + 5x2 – 7 is divided by x2 + x + 1
-
Show that x+4 is a factor of x3 + 6x2 - 7x - 60
-
Draw and locate the centroid of the triangle ABC where right angle at A, AB = 4cm and AC = 3cm
-
Determine whether the given set of points in each case are collinear or not (a, –2), (a, 3), (a, 0)
-
If (x, 3), (6, y), (8, 2) and (9, 4) are the vertices of a parallelogram taken in order, then find the value of x and y.
-
The median of observation 11,12,14,18, x+12, x+4, 30, 32, 35, 41 arrenged in ascending order is 24. Find the values of x.
-
For the measures in the figure, compute sine, cosine and tangent ratios of the angle \(\theta \)
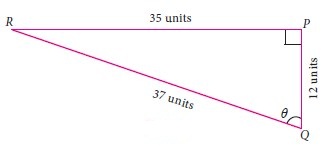
-
The total surface area of a cube is 864 cm2. Find its volume
-
Team I and Team II play 10 cricket matches each of 20 overs. Their total scores in each match are tabulated in the table as follows:
Match numbers 1 2 3 4 5 6 7 8 9 10 Team I 200 122 111 88 156 184 99 199 121 156 Team II 143 123 156 92 164 72 100 201 98 157 What is the relative frequency of Team I winning?
-
Factorise the following:
(i) (p - q2) - 6(p - q) -16
(ii) m2 + 2mm - 24n2
(iii) \(\sqrt{5}a^2+2a-3\sqrt5\)
(iv) a4- 3a2+ 2
(iv) 8m3- 2m2n -15mn2
(v) \({1\over x^2}+{1\over y^2}+{2\over xy}\) -
Find the quotient and remainder when 5x3 + 7x2 + 3x + 2 is divided by 3x + 2
-
Draw ΔPQR with sides PQ = 7 cm, QR = 8 cm and PR = 5 cm and construct its Orthocentre.
-
Find the angle of the given cyclic quadrilateral ABCD in the figure.
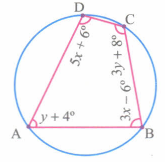
Part I
Answer all the questions.
Choose the most suitable answer from the given four alternatives and write the option code with the corresponding answer.
14 x 1 = 14
Part II
Answer any 10 questions. Question no. 28 is compulsory.
14 x 2 = 28
Part III
Answer any 10 questions. Question no. 42 is compulsory.
14 x 3 = 42
Part IV
Answer all the questions
4 x 5 = 20






 9th Standard Maths Syllabus
9th Standard Maths Syllabus  9th Standard Maths Study Materials
9th Standard Maths Study Materials

Reviews & Comments about 9th Standard Maths Annual Exam Model Question Paper III - 2019 - 2020
Write your Comment