Let A = {1,2,3,4} and B = { 2, 5, 8, 11,14} be two sets. Let f: A ⟶ B be a function given by f(x) = 3x − 1. Represent this function
(i) by arrow diagram
(ii) in a table form
(iii) as a set of ordered pairs
(iv) in a graphical form

Using horizontal line test (Fig.1.35(a), 1.35(b), 1.35(c)), determine which of the following functions are one – one.

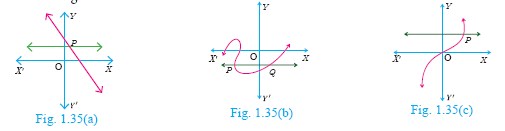
Let A = {1,2,3}, B = {4, 5, 6,7}, and f = {(1, 4),(2, 5),(3, 6)}  be a function from A to B. Show that f is one – one but not onto function.

If A = {-2, -1, 0, 1, 2} and f: A ⟶ B is an onto function defined by f(x) = x² + x + 1 then find B.

Let f be a function f : N ⟶ N be defined by f(x) = 3x + 2, x \(\in \) N
(i) Find the images of 1, 2, 3
(ii) Find the pre-images of 29, 53
(iii) Identify the type of function

Forensic scientists can determine the height (in cms) of a person based on the length of their thigh bone. They usually do so using the function h(b) = 2.47b + 54.10 where b is the length of the thigh bone.
(i) Check if the function h is one – one or not
(ii) Also find the height of a person if the length of his thigh bone is 50 cm.
(iii) Find the length of the thigh bone if the height of a person is 147.96 cm.

Let f be a function from R to R defined by f(x) = 3x - 5. Find the values of a and b given that (a,4) and (1,b) belong to f.

The distance S (in kms) travelled by a particle in time ‘t’ hours is given by S(t) = \(\frac { { t }^{ 2 }+t }{ 2 } \). Find the distance travelled by the particle after
(i) three and half hours.
(ii) eight hours and fifteen minutes.

If the function f: R⟶ R defined by 
\(f(x)=\left\{\begin{array}{l} 2 x+7, x<-2 \\ x^{2}-2,-2 \leq x<3 \\ 3 x-2, x \geq 3 \end{array}\right.\)
(i) f( 4)
(ii) f( -2)
(iii) f(4) + 2f(1)
(iv) \(\frac { f(1)-3f(4) }{ f(-3) } \)

Let f = {(2, 7); (3, 4), (7, 9), (-1, 6), (0, 2), (5,3)} be a function from A = {-1,0, 2, 3, 5, 7} to B = {2, 3, 4, 6, 7, 9}. Is this
(i) an one-one function
(ii) an onto function,
(iii) both one and onto function?

A function f: [-7,6) \(\rightarrow\) R is defined as follows.

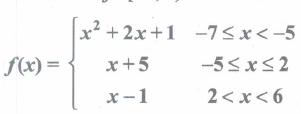
find 2f(-4) + 3f(2)

A function f: [-7,6) \(\rightarrow\) R is defined as follows.

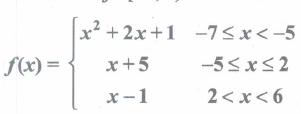
f(-7) - f(-3)

A function f: [-7,6) \(\rightarrow\) R is defined as follows.

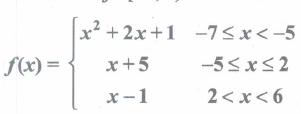
\(\cfrac { 4f(-3)+2f(4) }{ f(-6)-3f(1) } \)

f(x) = (1+ x)
g(x) = (2x - 1)
Show that fo(g(x)) = gof(x)

Let A = {1, 2, 3, 4, 5}, B = N and f: A \(\rightarrow\)B be defined by f(x) = x². Find the range of f. Identify the type of function.