New ! Physics MCQ Practise Tests



  1. Home
  2. 11th Standard
  3. Physics
  4. +1 Physics First Revision Test Model Question paper

Updated 11th Standard Physics Study Materials 2022-2023 Exams

+1 Physics First Revision Test Model Question paper Dec-27 , 2018

+1 First Revision Test Model

+1 Physics First Revision Test Model Question paper

+1 First Revision Test Model

11th Standard

    Reg.No. :
  •  
  •  
  •  
  •  
  •  
  •  

Physics

Time : 02:30:00 Hrs
Total Marks : 70

    I. Choose the most suitable answer:

    15 x 1 = 15

  1. The velocity of a particle v at an instant t is given by v = at + br2. The dimensions of b is

    (a)

    [L]

    (b)

    [LT-1]

    (c)

    [LT-2]

    (d)

    [LT-3]

  2. An object is dropped in an unknown planet from height 50 m, it reaches the ground in 2 s. The acceleration due to gravity in this unknown planet is

    (a)

    g = 20 ms-2

    (b)

    g = 25 ms-2

    (c)

    g = 15 ms-2

    (d)

    g = 30 ms-2

  3. The slope of the position-time graph will give ______________.

    (a)

    displacement

    (b)

    velocity

    (c)

    acceleration

    (d)

    force

  4. Two blocks of masses m and 2m are placed on a smooth horizontal surface as shown. In the first case only a force F1 is applied from the left. Later only a force F2 is applied from the right. If the force acting at the interface of the two blocks in the two cases is same, then F1 :F2 is

    (a)

    1:1

    (b)

    1:2

    (c)

    2:1

    (d)

    1:3

  5. A body of mass 4 m is lying in xy-plane at rest. It suddenly explodes into three pieces. Two pieces each of mass m move perpendicular to each other with equal speed v. The total kinetic energy generated due to explosion is

    (a)

    mv2

    (b)

    \(\frac{3}{2}\)mv2

    (c)

    2mv2

    (d)

    4mv2

  6. A disc of the moment of inertia Ia is rotating in a horizontal plane about its symmetry axis with a constant angular speed \(\omega\). Another disc initially at rest of moment of inertia Ib is dropped coaxially on to the rotating disc. Then, both the discs rotate with the same constant angular speed. The loss of kinetic energy due to friction in this process is,

    (a)

    \(\frac { 1 }{ 2 } \frac { { I }_{ b }^{ 2 } }{ 2({ I }_{ a }+{ I }_{ b }) } { \omega }^{ 2 }\)

    (b)

    \(\frac { { I }_{ b }^{ 2 } }{ ({ I }_{ a }+{ I }_{ b }) } { \omega }^{ 2 }\)

    (c)

    \(\frac { { ({ I }_{ b }-{ I }_{ a }) }^{ 2 } }{ ({ I }_{ a }+{ I }_{ b }) } { \omega }^{ 2 }\)

    (d)

    \(\frac { 1 }{ 2 } \frac { { { I }_{ b }{ I }_{ b } } }{ ({ I }_{ a }+{ I }_{ b }) } { \omega }^{ 2 }\)

  7. Three identical metal balls, each of the radius r are placed touching each ether on a horizontal surface such that an equilateral triangle is formed when centres of three balls are joined. The centre of the mass of the system is located at _____________.

    (a)

    line joining centres of any two balls

    (b)

    centre of one of the balls

    (c)

    horizontal surface

    (d)

    point of intersection of the medians

  8. The work done by Sun on Earth at any finite interval of time is

    (a)

    Positive, negative or zero

    (b)

    Strictly positive

    (c)

    Strictly negative

    (d)

    It is always zero

  9. Which of the following is not a scalar?

    (a)

    viscosity

    (b)

    surface tension

    (c)

    pressure

    (d)

    stress

  10. If there were no gravity, which of the following will not be there for a fluid?

    (a)

    viscosity

    (b)

    surface tension

    (c)

    pressure

    (d)

    archimedes upward thrust

  11. An ideal refrigerator has a freezer at temperature −12°C. The coefficient of performance of the engine is 5. The temperature of the air (to which the heat ejected) is

    (a)

    50°C

    (b)

    45.2°C

    (c)

    40.2°C

    (d)

    37.5°C

  12. Which of the following shows the correct relationship between the pressure and density of an ideal gas at constant temperature?

    (a)

    (b)

    (c)

    (d)

  13. An ideal spring of spring constant k, is suspended from the ceiling of a room and a block of mass M is fastened to its lower end. If the block is released when the spring is un-stretched, then the maximum extension in the spring is

    (a)

    4\(\frac { Mg }{ k } \)

    (b)

    \(\frac { Mg }{ k } \)

    (c)

    2\(\frac { Mg }{ k } \)

    (d)

    \(\frac { Mg }{ 2k } \)

  14. Which of the following function represents a simple harmonic oscellation?

    (a)

    sin ωt - cos ωt

    (b)

    sin ωt + sin2 ωt

    (c)

    sin ωt - sin2 ωt

    (d)

    sin2 ωt

  15. A sound wave whose frequency is 5000 Hz travels in air and then hits the water surface. The ratio of its wavelengths in water and air is

    (a)

    4.30

    (b)

    0.23

    (c)

    5.30

    (d)

    1.23

    16. II. Answer any six questions. Q.No 18 is compulsory:

    6 x 2 = 12

  16. Name the instrument to measure Sub-atomic particles.

  17. If the position vector of the particle is given by \(\vec { r } ={ 3t }^{ 2 }\hat { i } +5t\hat { j } +4\hat { k } \), Find the
    (a) The velocity of the particle at t = 3 s
    (b) Speed of the particle at t = 3 s
    (c) Acceleration of the particle at time t = 3s

  18. A bob attached to the string oscillates back and forth. Resolve the forces acting on the bob into components. What is the acceleration experience by the bob at an angle ፀ.

  19. A lighter body collides with much more massive body at rest. Prove that the direction of lighter body is reversed and massive body remains at rest.

  20. Write the relation between angular momentum and rotational kinetic energy. Draw a graph for the same. For two objects of same angular momentum, compare the moment of inertia using the graph.

  21. What is Reynold’s number? Give its significance.

  22. What is a black body?

  23. Explain damped oscillation. Give an example.

  24. What is meant by reverberation time?

    25. III. Answer any six questions. Q. No 33 is compulsory:

    6 x 3 = 18

  25. Give the values for the following units with prefixes.
    (i) 1 Mega ohm
    (ii) 1 milliampere
    (iii) 1deca gram
    (iv) 1nano second
    (v) 1 micro volt
    (vi) 1 centimetre

  26. Write down the kinematic equations for angular motion.

  27. What is the meaning by 'pseudo force'?

  28. A ball of mass m is pushed down the wall of hemispherical bowl from point A. It just rises up to edge Q of the bowl. Find the speed at which baU is pushed down.

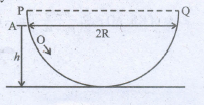
  29. Can a body be in equilibrium while in motion? If yes, give an example.

  30. Determine gravitational potential from gravitational potential energy?

  31. Discuss the limits of the specific heat of a gas

  32. Explain how does a gas exert pressure on the bases of kinetic theory of gases.

  33. Calculate the velocity of the travelling pulse as shown in the figure below. The linear mass density of pulse is 0.25 kg m-1. Further, compute the time taken by the travelling pulse to cover a distance of 30 cm on the string.

    34. IV. Answer all in detail

    7 x 5 = 35

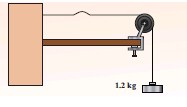
    1. The force F acting on a body moving in a circular path depends on mass of the body (m), velocity (v) and radius (r) of the circular path. Obtain the expression for the force by dimensional analysis method. (Take the value of k = 1)

    2. Derive the equation of motion, range and maximum height reached by the particle thrown at an oblique angle \(\theta\) with respect to the horizontal direction.

    1. A body falling freely descends 0.3m in 0.1s and 0.398m in the next 0.1s in some other planet. Find the value of g in that planet.

    2. An object of mass 10 kg moving with a speed of 15 ms-1 hits the wall and comes to rest within
      (a) 0.03 second
      (b) 10 second.
      Calculate the impulse and average force acting on the object in both the cases.

    1. Derive an expression for the velocity of the body moving in a vertical circle. And also find a tension at the bottom and the top of the circle.

    2. State in the absence of any external force the velocity of the centre of mass remains constant.

    1. Three mutually perpendicular beams AB, OC, GH are fixed to form a structure which is fixed to the ground firmly as shown in the Figure. One string is tied to the point C and its free end D is pulled with a force F. Find the magnitude and direction of the torque produced by the force,
      (i) about the points D, C, O and B
      (ii) about the axis CD, OC, AB and GH.

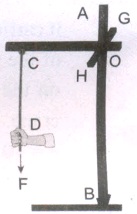
    2. Consider four masses m1, m2, m3, and m4 arranged on the circumference of a circle as shown in figure below.

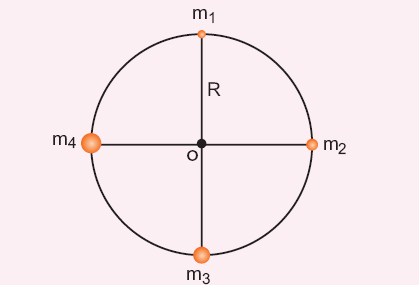
      Calculate
      (a) The gravitational potential energy of the system of 4 masses shown in figure.
      (b) The gravitational potential at the point O due to all the 4 masses

    1. Explain briefly about the graphical representation of Displacement, velocity and acceleration in SHM.

    2. How does the wave y = sin(x − a) for a = 0, a =\(\frac { \pi }{ 4 } ,a=\frac { \pi }{ 2 } ,a=\frac { 3\pi }{ 2 } \) and a = \(\pi\) look like? Sketch this wave.

*****************************************

Reviews & Comments about +1 Physics First Revision Test Model Question paper

Write your Comment