CBSE 12th Standard Maths Subject Linear Programming Case Study Questions 2021
By QB365
QB365 Provides the updated CASE Study Questions for Class 12 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Maths Linear Programming Case Study Questions 2021
12th Standard CBSE
-
Reg.No. :
Maths
-
Linear programming is a method for finding the optimal values (maximum or minimum) of quantities subject to the constraints when relationship is expressed as linear equations or inequations.
Based on the above information, answer the following questions.
(i) The optimal value of the objective function is attained at the points(a) on X-axis (b) on Y-axis (c) which are corner points of the feasible region (d) none of these (ii) The graph of the inequality 3x + 4y < 12 is
(a) half plane that contains the origin (b) half plane that neither contains the origin nor the points of the line 3x + 4y =12. (c) whole XOY-plane excluding the points on line 3x + 4y = 12 (d) none of these (iii) The feasible region for an LPP is shown in the figure. Let Z = 2x + 5y be the objective function. Maximum of Z occurs at
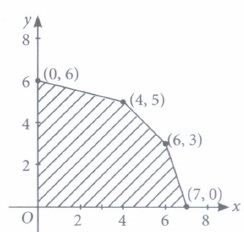
(a) (7,0) (b) (6,3) (c) (0,6) (d) (4,5) (iv) The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5), (15, 15), (0, 20). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20) is
(a) p = q (b) p = 2q (c) q=2p (d) q=3p (v) The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20,40), (60,20), (60, 0). The objective function is Z = 4x + 3y. Compare the quantity in Column A and Column B
Column A Column B Maximum of Z 325 (a) The quantity in column A is greater (b) The quantity in column B is greater (c) The two quantities are equal (d) The relationship cannot be determined on the basis of the information supplied (a) -
Deepa rides her car at 25 km/hr, She has to spend Rs. 2 per km on diesel and if she rides it at a faster speed of 40 km/hr, the diesel cost increases to Rs. 5 per km. She has Rs. 100 to spend on diesel. Let she travels x kms with speed 25 km/hr and y kms with speed 40 km/hr. The feasible region for the LPP is shown below:
Based on the above information, answer the following questions
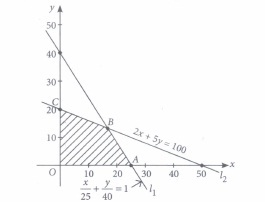
Based on the above information, answer the following questions.
(i) What is the point of intersection of line l1 and l2,\(\text { (a) }\left(\frac{40}{3}, \frac{50}{3}\right)\) \(\text { (b) }\left(\frac{50}{3}, \frac{40}{3}\right)\) \(\text { (c) }\left(\frac{-50}{3}, \frac{40}{3}\right)\) \(\text { (d) }\left(\frac{-50}{3}, \frac{-40}{3}\right)\) (ii) The corner points of the feasible region shown in above graph are
\(\text { (a) }(0,25),(20,0),\left(\frac{40}{3}, \frac{50}{3}\right)\) \(\text { (b) }(0,0),(25,0),(0,20)\) \(\text { (c) }(0,0),\left(\frac{40}{3}, \frac{50}{3}\right),(0,20)\) \(\text { (d) }(0,0),(25,0),\left(\frac{50}{3}, \frac{40}{3}\right),(0,20)\) (iii) If Z = x + y be the objective function and max Z = 30. The maximum value occurs at point
\(\text { (a) }\left(\frac{50}{3}, \frac{40}{3}\right)\) (b) (0, 0) (c) (25, 0) (d) (0, 20) (iv) If Z = 6x - 9y be the objective function, then maximum value of Z is
(a) -20 (b) 150 (c) 180 (d) 20 (v) If Z = 6x + 3y be the objective function, then what is the minimum value of Z?
(a) 120 (b) 130 (c) 0 (d) 150 (a) -
Corner points of the feasible region for an LPP are (0, 3), (5, 0), (6, 8), (0, 8). Let Z = 4x - 6y be the objective function.
Based on the above information, answer the following questions.
(i) The minimum value of Z occurs at(a) (6, 8) (b) (5, 0) (c) (0, 3) (d) (0, 8) (ii) Maximum value of Z occurs at
(a) (5, 0) (b) (0, 8) (c) (0, 3) (d) (6, 8) (iii) Maximum of Z - Minimumof Z =
(a) 58 (b) 68 (c) 78 (d) 88 (iv) The corner points of the feasible region determined by the system of linear inequalities are
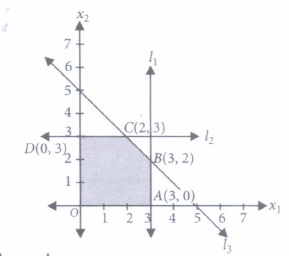
(a) (0, 0), (-3, 0), (3, 2), (2, 3) (b) (3, 0), (3, 2), (2, 3), (0, -3) (c) (0, 0), (3, 0), (3, 2), (2, 3), (0, 3) (d) None of these (v) The feasible solution of LPP belongs to
(a) first and second quadrant (b) first and third quadrant (c) only second quadrant (d) only first quadrant (a) -
Suppose a dealer in rural area wishes to purpose a number of sewing machines. He has only Rs. 5760 to invest and has space for at most 20 items for storage. An electronic sewing machine costs him Rs. 360 and a manually operated sewing machine Rs. 240. He can sell an electronic sewing machine at a profit of Rs. 22 and a manually operated sewing machine at a profit of Rs. 18.
Based on the above information, answer the following questions.
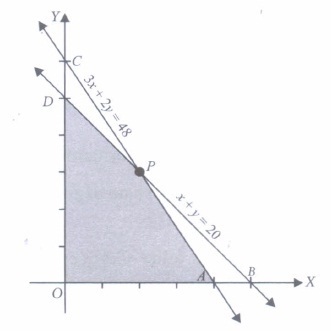
(i) Let x and y denotes the number of electronic sewing machines and manually operated sewing machines purchased by the dealer. If it is assume that the dealer purchased atleast one of the given machines, then(a) x + y ≥ 0 (b) x + y < 0 (c) x + y > 0 (d) x + y ≤ 0 (ii) Let the constraints in the given problem is represented by the following inequalities
x + y ≤ 20
360x + 240y ≤ 5760
x, y ≥ 0
Then which of the following point lie in its feasible region.(a) (0, 24) (b) (8, 12) (c) (20, 2) (d) None of these (iii) If the objective function of the given problem is maximise z = 22x + 18y, then its optimal value occur at
(a) (0, 0) (b) (16, 0) (c) (8, 12) (d) (0, 20) (iv) Suppose the following shaded region APDO, represent the feasible region corresponding to mathematical formulation. of given problem. Then which of the following represent the coordinates of one of its corner points.
(a) (0, 24) (b) (12, 8) (c) (8, 12) (d) (6, 14) (v) If an LPP admits optimal solution at two consecutive vertices of a feasible region, then
(a) the required optimal solution is at the midpoint of the line joining two points. (b) the optimal solution occurs at every point on the line joining these two points. (c) the LPP under consideration is not solvable. (d) the LPP under consideration must be reconstructed. (a) -
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to, constraints described by linear inequalities, this optimal value must occur at a corner point (vertex) of the feasible region.
Based on the above information, answer the following questions.
(i) Objective function of a L.P.P. is(a) a constant (b) a function to be optimised (c) a relation between the variables (d) none of these (ii) Which of the following statement is correct?
(a) Every LPP has at least one optimal solution. (b) Every LPP has a unique optimal solution. (c) If an LPP has two optimal solutions, then it has infinitely many solutions (d) none of these (iii) In solving the LPP : "minimize f = 6x + 10y subject to constraints x ≥ 6, Y ≥ 2, 2x + y ≥ 10,x ≥ 0,y ≥ 0" redundant constraints are
(a) x ≥ 6, y ≥ 2 (b) 2x + y ≥ 10, x ≥ 0, y ≥ 0 (c) x ≥ 6 (d) none of these (iv) The feasible region for a LPP is shown shaded in the figure. Let Z = 3x - 4y be the objective function. Minimum of Z occurs at
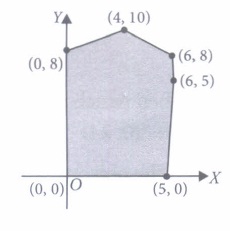
(a) (0, 0) (b) (0, 8) (c) (5, 0) (d) (4, 10) (v) The feasible region for a LPP is shown shaded in the figure. Let F = 3x - 4y be the objective function. Maximum value of F is
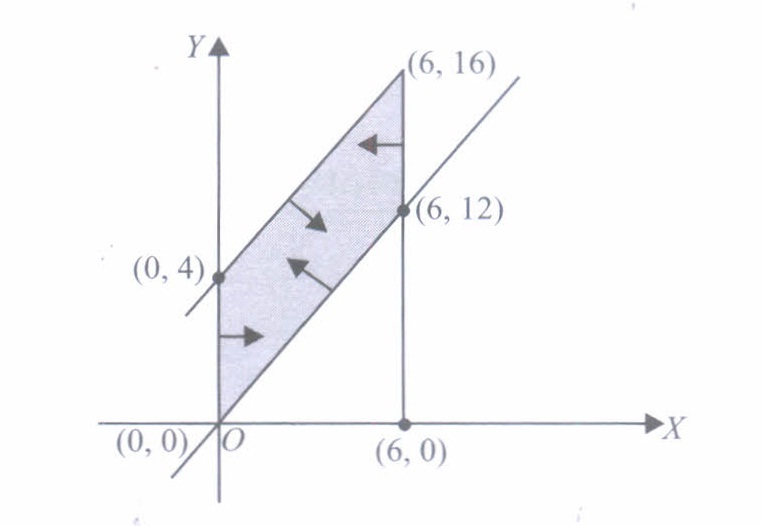
(a) 0 (b) 8 (c) 12 (d) -18 (a)
Case Study Questions