CBSE 12th Standard Maths Subject Three Dimensional Geometry Case Study Questions With Solution 2021
By QB365
QB365 Provides the updated CASE Study Questions for Class 12 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 12th Standard Maths Subject Three Dimensional Geometry Case Study Questions With Solution 2021
12th Standard CBSE
-
Reg.No. :
Maths
-
Two motorcycles A and B are running at the speed more than allowed speed on the road along the lines \(\vec{r}=\lambda(\hat{i}+2 \hat{j}-\hat{k}) \text { and } \vec{r}=3 \hat{i}+3 \hat{j}+\mu(2 \hat{i}+\hat{j}+\hat{k})\), respectively.

Based on the above information, answer the following questions.
(i) The cartesian equation of the line along which motorcycle A is running, is(a) \(\frac{x+1}{1}=\frac{y+1}{2}=\frac{z-1}{-1}\) (b) \(\frac{x}{1}=\frac{y}{2}=\frac{z}{-1}\) (c) \(\frac{x}{1}=\frac{y}{2}=\frac{z}{1}\) (d) none of these (ii) The direction cosines of line along which motorcycle A is running, are
(a) < 1, -2, 1 > (b) < 1, 2, -1 > (c) \(<\frac{1}{\sqrt{6}}, \frac{-2}{\sqrt{6}}, \frac{1}{\sqrt{6}}>\) (d) \(<\frac{1}{\sqrt{6}}, \frac{2}{\sqrt{6}}, \frac{-1}{\sqrt{6}}>\) (iii) The direction ratios of line along which motorcycle B is running, are
(a) < 1, 0, 2 > (b) < 2, 1, 0 > (c) < 1, 1, 2 > (d) < 2, 1, 1 > (iv) The shortest distance between the gives lines is
(a) 4 units (b) 2.\(\sqrt 3\) units (c) 3.\(\sqrt 2\) units (d) 0 units (v) The motorcycles will meet with an accident at the point
(a) (-1, 1, 2) (b) (2, 1, -1) (c) (1, 2, -1) (d) does not exist (a) -
Consider the following diagram, where the forces in the cable are given.
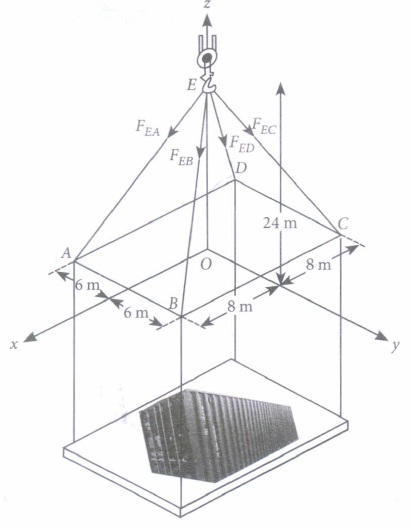
Based on the above information, answer the following questions.
(i) The cartesian equation of line along EA is\((a) \ \frac{x}{-4}=\frac{y}{3}=\frac{z}{12}\) \((b) \ \frac{x}{-4}=\frac{y}{3}=\frac{z-24}{12}\) \((c) \ \frac{x}{-3}=\frac{y}{4}=\frac{z-12}{12}\) \((d) \ \frac{x}{3}=\frac{y}{4}=\frac{z-24}{12}\) (ii) The vector \(\overline{E D}\) is
(a) \(8 \hat{i}-6 \hat{j}+24 \hat{k}\) (b) \(-8 \hat{i}-6 \hat{j}+24 \hat{k}\) (c) \(-8 \hat{i}-6 \hat{j}-24 \hat{k}\) (d) \(8 \hat{i}+6 \hat{j}+24 \hat{k}\) (iii) The length of the cable EB is
(a) 24 units (b) 26 units (c) 27 units (d) 25 units (iv) The length of cable EC is equal to the length of
(a) EA (b) EB (c) ED (d) All of these (v) The sum of all vectors along the cables is
(a) \(96 \hat{i}\) (b) \(96 \hat{j}\) (c) \(-96 \hat{k}\) (d) \(96 \hat{k}\) (a) -
Suppose the floor of a hotel is made up of mirror polished Kota stone. Also, there is a large crystal chandelier attached at the ceiling of the hotel. Consider the floor of the hotel as a plane having equation x - 2y + 2z = 3 and crystal chandelier at the point (3, -2, 1).

Based on the above information, answer the following questions.
(i) The d.r's of the perpendicular from the point (3, -2, 1) to the plane x - 2y + 2z = 3, is(a) < 1,2,2 > (b) < 1, - 2, 2 > (c) < 2,1,2 > (d) < 2, -1, 2 > (ii) The length of the perpendicular from the point (3, -2, 1) to the plane x - 2y + 2z = 3, is
(a) \(\frac{2}{3}\)units (b) 3 units (c) 2 units (d) none of these (iii) The equation of the perpendicular from the point (3, -2, 1) to the plane x - 2y + 2z = 3, is
(a) \(\frac{x-3}{1}=\frac{y-2}{-2}=\frac{z-1}{2}\) (b) \(\frac{x-3}{1}=\frac{y+2}{-2}=\frac{z-1}{2}\) (c) \(\frac{x+3}{1}=\frac{y+2}{-2}=\frac{z-1}{2}\) (d) none of these (iv) The equation of plane parallel to the plane x - 2y + 2z = 3, which is at a unit distance from the point (3, -2, 1) is
(a) x - 2y + 2z = 0 (b) x - 2y + 2z = 6 (c) x - 2y + 2z = 12 (d) Both (b) and (c) (v) The image of the point (3, -2, 1) in the given plane is
(a) \(\left(\frac{5}{3}, \frac{2}{3}, \frac{-5}{3}\right)\) (b) \(\left(\frac{-5}{3}, \frac{-2}{3}, \frac{5}{3}\right)\) (c) \(\left(\frac{-5}{3}, \frac{2}{3}, \frac{5}{3}\right)\) (d) none of these (a) -
In a diamond exhibition, a diamond is covered in cubical glass box having coordinates 0(0, 0, 0), A(1, 0, 0), B(1, 2, 0), C(0, 2, 0), O'(0,0,3), A'(1, 0, 3), B'(1, 2, 3) and C(0, 2, 3).
Based on the above information, answer the following questions.
(i) Direction ratios of OA are(a) < 0, 1, 0 > (b) <1, 0, 0> (c) < 0, 0, 1 > (d) none of these (ii) Equation of diagonal OB' is
(a) \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\) (b) \(\frac{x}{0}=\frac{y}{1}=\frac{z}{2}\) (c) \(\frac{x}{1}=\frac{y}{0}=\frac{z}{2}\) (d) none of these (iii) Equation of plane OABC is
(a) x = 0 (b) y = 0 (c) z = 0 (d) none of these (iv) Equation of plane O' A' B' C is
(a) x = 3 (b) y = 3 (c) z = 3 (d) z = 2 (v) Equation of plane ABB' A' is
(a) x = 1 (b) y = 1 (c) z = 2 (d) x = 3 (a) -
The equation of motion of a rocket are: x = 2t, y = -4t, z = 4t, where the time 't' is given in seconds, and the distance measured is in kilometres.
Based on the above information, answer the following questions.
(i) What is the path of the rocket?(a) Straight line (b) Circle (c) Parabola (d) none of these (ii) Which of the following points lie on the path of the rocket?
(a) (0, 1, 2) (b) (1, -2, 2) (c) (2, -2, 2) (d) none of these (iii) At what distance will the rocket be from the starting point (0, 0, 0) in 10 seconds?
(a) 40 km (b) 60 km (c) 30 km (d) 80 km (iv) If the position of rocket at certain instant of time is (3, -6, 6), then what will be the height of the rocket from the ground, which is along the xy-plane?
(a) 3km (b) 2km (c) 4km (d) 6km (v) At certain instant of time, if the rocket is above sea level, where equation of surface of sea is given by 3x - y + 4z = 2 and position of rocket at that instant of time is (1, -2,2), then the image of position of rocket in the sea is
(a) \(\left(\frac{20}{13}, \frac{15}{13}, \frac{18}{13}\right)\) (b) \(\left(\frac{-20}{13}, \frac{-15}{13}, \frac{-18}{13}\right)\) (c) \(\left(\frac{20}{13}, \frac{-15}{13}, \frac{18}{13}\right)\) (d) none of these (a)
Case Study Questions