Electrostatic potential energy of a system of point charges is defined as the total amount of work done in bringing the different charges to their respective positions from infinitely charge mutual separations. The work is stored in the system of two point charges in the form of electrostatic potential energy U of the system. Electric potential difference between any points A and B in an electric field is the amount of work done in moving a unit positive test charge from A to B along any path agents the electrostatic force
\(V_{B}-V_{A}=\frac{W_{A B}}{q_{0}}=\int \mid \vec{E} \cdot d l\)

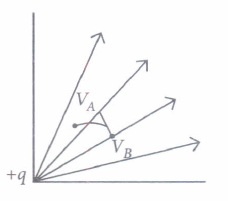
(i) A test charge is moved from lower potential point to a higher potential point. The potential energy of test charge will

(ii) Which of the following statement is not true?

(iii) Work done in moving a charge from one point to another inside a uniformly charged conducting sphere is

(iv) The work done in bringing a unit positive charge from infinite distance to a point at distance x from a positive charge Q is W. Then the potential \(\phi\) at that point is

(v) If \(1 \mu C\) charge is shifted from A to B and it is found that work done by an external force is \(40 \mu \mathrm{J}\). In doing so against electrostatics force, the potential difference V_A- V_B is 

Potential difference (\(\Delta\)V) between two points A and B separated by a distance x, in a uniform electric field E is given by \(\Delta V=-E x\),where x is measured parallel to the field lines. If a charge qo moves from P to Q, the changein potential energy \((\Delta U)\) is given as \(\Delta U=q_{0} \Delta V .\) A proton is released from rest in uniform electric field of magnitude \(4.0 \times 10^{8} \mathrm{Vm}^{-1}\) directed along the positive X-axis. The proton undergoes a displacement of 0.25 m in the direction of E.
Mass of a proton = 1.66 x 10^-27 kg and charge of proton = 1.6 x10^-19 C

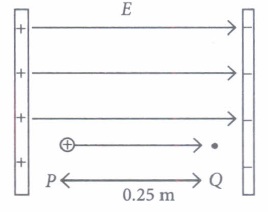
(i) The change in electric potential of the proton between the points A and B is

(ii) The change in electric potential energy of the proton for displacement from A to B is

(iii) The mutual electrostatic potential energy between two protons which are at a distance of 9 x 10^-15 m, in \({ }_{92} \mathrm{U}^{235}\) nucleus is

(iv) If a system consists of two charges 4 mC and -3mC with no external field placed at (-5 em, 0, 0) and (5 em, 0, 0) respectively. The amount of work required to separate the two charges infinitely away from each other is

(v) As the proton moves from P to Q, then

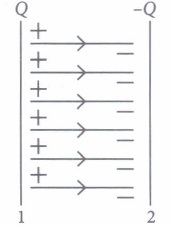
The potential at any observation point P of a static electric field is defined as the work done by the external agent (or negative of work done by electrostatic field) in slowly bringing a unit positive point charge from infinity to the observation point. Figure shows the potential variation along the line of charges. Two point charges Q₁ and Q₂ lie along a line at a distance from each other.

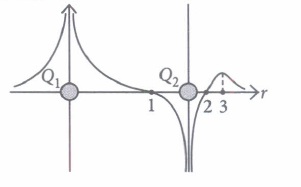
(i) At which of the points 1, 2 and 3 is the electric field is zero?

(ii) The signs of charges Q₁ and Q₂ respectively are

(iii) Which of the two charges Q₁ and Q₂ is greater in magnitude?

(iv) Which of the following statement is not true?

(v) Positive and negative point charges of equal magnitude are kept at \(\left(0,0, \frac{a}{2}\right)\) and \(\left(0,0, \frac{-a}{2}\right)\) respectively.
The work done by the electric field when another positive point charge is moved from (-a, 0, 0) to (0, a, 0) is

For the various charge systems, we represent equipotential surfaces by curves and line of force by full line curves. Between any two adjacent equipotential surfaces, we assume a constant potential difference the equipotential surfaces of a single point charge are concentric spherical shells with their centres at the point charge. As the lines of force point radially outwards, so they are perpendicular to the equipotential surfaces at all points.

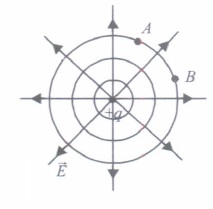
(i) Identify the wrong statement.

(ii) Nature of equipotential surface for a point charge is

(iii) A spherical equipotential surface is not possible

(iv) The work done in carrying a charge q once round a circle of radius a with a charge Q at its centre is

(v) The work done to move a unit charge along an equipotential surface from P to Q

This energy possessed by a system of charges by virtue of their positions. When two like charges lie infinite distance apart, their potential energy is zero because no work has to be done in moving one charge at infinite distance from the other.
In carrying a charge q from point A to point B, work done \(W=q\left(V_{A}-V_{B}\right)\). This work may appear as change in KE/PE of the charge. The potential energy of two charges q₁ and q₂ at a distance r in air is \(\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} r}\). It is measured in joule. It may be positive, negative or zero depending on the signs of q_l and q₂.
(i) Calculate work done in separating two electrons form a distance of 1m to 2m in air, where e is electric charge and k is electrostatic force constant.

(ii) Four equal charges q each are placed at four corners of a square of side a each. Work done in carrying a charge -q from its centre to infinity is

(iii) Two points A and B are located in diametrically opposite directions of a point charge of +2 \(\mu \mathrm{C}\) at distances 2 m and 1 m respectively from it. The potential difference between A and B is 

(iv) Two point charges A = +3 nC and B = +1 nC are placed 5 ern apart in air. The work done to move charge B towards A by 1 cm is

(v) A charge Q is placed at the origin. The electric potential due to this charge at a given point in space is V. The work done by an external force in bringing another charge q from infinity up to the point is

The electrical capacitance of a conductor is the measure of its ability to hold electric charge. An isolated spherical conductor of radius R. The charge Q is uniformly distributed over its entire surface. It can be assumed to be concentrated at the centre of the sphere. The potential atany point on the surface of the spherical conductor will be \(V=\frac{1}{4 \pi \varepsilon_{0}} \frac{Q}{R}\).

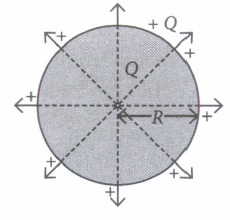
Capacitance of the spherical conductor situated in vacuum is \(C=\frac{Q}{V}=\frac{Q}{\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{Q}{R}} \text { or } C=4 \pi \varepsilon_{0} R\) Clearly, the capacitance of a spherical conductor is proportional to its radius.
The radius of the spherical conductor of 1F capacitance is R = \(\frac{1}{4 \pi \varepsilon_{0}}\). C and this radius is about 1500 times the radius of the earth \(\left(\sim 6 \times 10^{3} \mathrm{~km}\right)\).
(i) If an isolated sphere has a capacitance 50pF. Then radius is

(ii) How much charge should be placed on a capacitance of 25 pF to raise its potential to l0⁵ V?

(iii) Dimensions of capacitance is

(iv) Metallic sphere of radius R is charged to potential V. Then charge q is proportional to

(v) If 64 identical spheres of charge q and capacitance C each are combined to form a large sphere. The charge and capacitance of the large sphere is

The simplest and the most widely used capacitor is the parallel plate capacitor. It consists of two large plane parallel conducting plates, separated by a small distance.
In the outer regions above the upper plate and below the lower plate, the electric fields due to the two charged plates cancel out. The net field is zero.
In the inner region between the two capacitor plates, the electric fields due to the two charged plates add up. The net field is \(\frac{\sigma}{\varepsilon_{0}}\).

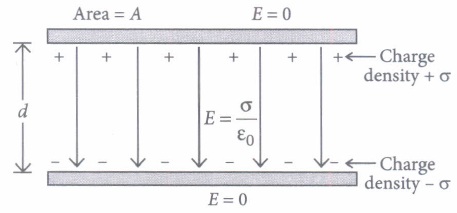
For a uniform electric field, potential difference between the plates = Electric field x distance between the plates. Capacitance of the parallel plate capacitor is, the charge required to supplied to either of the conductors of the capacitor so as to increase the potential difference between then by unit amount.
(i) A parallel plate capacitor is charged and then isolated. The effect of increasing the plate separation on charge, potential and capacitance respectively are

(ii) In a parallel plate capacitor, the capacity increases if

(iii) A parallel plate capacitor has two square plates with equal and opposite charges. The surface charge densities on the plates are \(+\sigma\) and \(-\sigma\) respectively. In the region between the plates the magnitude of the electric field is

(iv) If a parallel plate air capacitor consists of two circular plates of diameter 8 cm. At what distance should the plates be held so as to have the same capacitance as that of sphere of diameter 20 cm?

(v) If a charge of + 2.0 x 10^-8 C is placed on the positive plate and a charge of -1.0 x 10^-8 C on the negative plate of a parallel plate capacitor of capacitance 1.2 x 10^-3 \(\mu \mathrm{F}\) then the potential difference developed between the plates is

A dielectric slab is a substance which does not allow the flow of charges through it but permits them to exert electrostatic forces on one another.
When a dielectric slab is placed between the plates, the field E_o polarises the dielectric. This induces charge -Q_p on the upper surface and + Q_p on the lower surface of the dielectric. These induced charges set up a field E_p inside the dielectric in the opposite direction of \(\vec{E}_{0}\) as shown.

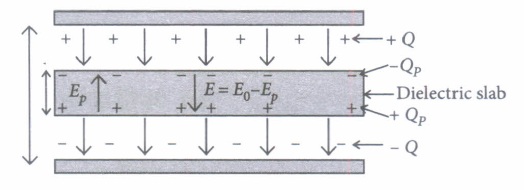
(I) In a parallel plate capacitor, the capacitance increases from \(4 \mu \mathrm{F}\) to 80\(\mu \mathrm{F}\) on introducing a dielectric medium between the plates. What is the dielectric constant of the medium?

(ii) A parallel plate capacitor with air between the plates has a capacitance of 8 pF. The separation between the plates is now reduced half and the space between them is filled with a medium of dielectric constant 5.
Calculate the value of capacitance of the capacitor in second case.

(iii) A dielectric introduced between the plates of a parallel plate condenser

(iv) A parallel plate capacitor of capacitance 1 pF has separation between the plates is d. When the distance of separation becomes 2d and wax of dielectric constant x is inserted in it the capacitance becomes 2 pF. What is the value of x?

(v) A parallel plate capacitor having area A and separated by distance d is filled by copper plate of thickness b. The new capacity is

A capacitor is a device to store energy. The process of charging up a capacitor involves the transferring of electric charges from its one place to another. This work done in charging the capacitor is stored as its electrical potential energy.

If q is the charge and V is the potential difference across a capacitor at any instant during its charging, then small work done in storing an additional small charge dq against the repulsion of charge q already stored on it is \(d W=V . d q=(q / C) d q\)
(i) A system of 2 capacitors of capacitance \(2 \mu \mathrm{F}\) and \(4 \mu \mathrm{F}\) is connected in series across a potential difference of 6 V. The energy stored in the system is

(ii) A capacitor of capacitance of \(10 \mu \mathrm{F}\) is charged to 10 V. The energy stored in it is

(iii) A parallel plate air capacitor has capacity C farad, potential V volt and energy E joule. When the gap between the plates is completely filled with dielectric

(iv) A capacitor with capacitance \(5 \mu \mathrm{F}\) is charged to \(5 \mu \mathrm{C}\). If the plates are pulled apart to reduce the capacitance to \(2 \mu \mathrm{F}\),how much work is done?

(v) A metallic sphere of radius 18 cm has been given a charge of 5 x 10^-6 C. The energy of the charged conductor is

When an insulator is placed in an external field, the dipoles become aligned. Induced surface charges on the insulator establish a polarization field \(\vec{E}_{i}\) in its interior. The net field \(\vec{E}\) in the insulator is the vector sum of \(\vec{E}_{0}\) and \(\vec{E}_{i}\) as shown in the figure.

On the application of external electric field, the effect of aligning the electric dipoles in the insulator is called polarisation and the field \(\vec{E}_{i}\) is known as the polarisation field.
The dipole moment per unit volume of the dielectric is known as polarisation \((\vec{P})\).
For linear isotropic dielectrics, \(\vec{P}=\chi \vec{E}\) where X = electrical susceptibility of the dielectric medium.
(i) Which among the following is an example of polar molecule?

(ii) When air is replaced by a dielectric medium of constant K, the maximum force of attraction between two charges separated by a distance

(iii) Which of the following is a dielectric?

(iv) For a polar molecule, which of the following statements is true?

(v) When a comb rubbed with dry hair attracts pieces of paper. This is because the

Consider a conducting sphere SI of radius 20 em. A positive charge is given to it so that maximum electric field on it is 2.0 x 10⁴ N/C. The same amount of negative charge is given to another isolated conducting hollow sphere of radius 40 cm, If one shell is now placed inside another so that they are both concentric as shown below. Now answer the following questions:

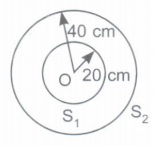
(i) The electric field intensity just inside the outer sphere is __________
(ii) The electrostatic potential at any point inside sphere S₁ is _______
(iii) If sphere S₁ and S₂ are joined by a wire, then what will happen?

Electric field between oppositely charged parallel conducting plates:
When two plane parallel conducting plates, having the size and spacing shown in figure given below are given equal and opposite charges, the field between and around them is approximately as shown, while most of the charge accumulates at the opposing faces of the plates and the field is essentially uniform in the space between them, there is a small quantity of charge on the outer surfaces of the plates and a certain spreadwing or fringing of the field at the edges of the plates.
As the plates are made larger and the distance between them diminished, the fringing becomes relatively less. This kind of arrangement is called capacitors.
Now if two plates are separated by a distance '3d', and are maintained at a potential difference' V' then answer the following questions.

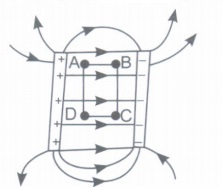
(i) What is the use of capacitors?
(ii) If two protons are placed at points A and B respectively, then which one will experience more force?

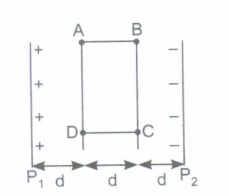
(iii) When both the protons are released then which one will gain more K.E. just before striking the -ve plate?
(iv) If one proton is moved along
(a) A to B
(b) B to C
(c) C to D
(d) Along ABCD, then how much work is done by external agent?
(v) Which property of electric field is shown by answer to (iv) (d) part?

Although a single piece of an isolated conductor can store charge on its surface.
Ability to store charge is called capacitance (C). If Q is the charge and potential V then
\(C=\frac{Q}{V}\)               ..........(i)
If we increase charge, potential on the surface increases, we can store charge only upto some maximum value which is due to some limited maximum potential. Hence, instead of one conducor we use two conductors to form a capacitor, so that more charge can be stored.
(i) What is the capacitance of earth. Radius of earth = R = 6.4 x 10⁶ m
(ii) An uncharged insulated conductor A is brought near a charged insulated conductor B. What happens to charge and potential of B?
(iii) What will happen if potential of conductor exceeds its maximum value, so that electric field becomes 3 x 10⁶ V/m in air.
(iv) On what factors capacitance depends?

A student charged the capacitors of capacitances 2\(\mu\)F and 3\(\mu\)F to potential of 100V each separately. Now he connected positive plate of A to negative plate of B and negative plate of A to positive plate of B.

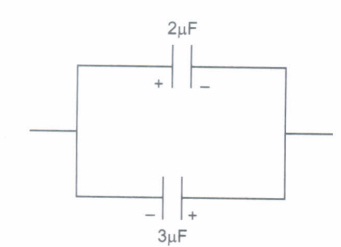
Now answer the following questions:
(i) Determine energy stored in each capacitor.
(ii) What is their common potential after joining?
(iii) Find charge on capacitor A after joining.
(iv) What is the loss of energy in this process?

Two small charged metal spheres A and Bare situated in a vacuum. The distance between the centres of the sphere is 10 cm. Electric charge on each sphere may be assumed to be a point charge at the centre P of the sphere and is equal to 10^{- 9} C each. Point P is a movable point that lies on the line joining the centres of the two charged spheres and is at a distance x from the centre of sphere A.
(i) Draw the variation of electric field E with distance x as point P moves towards sphere B.
(ii) Also draw the variation of electric potential vs distance x as point P moves towards B.
(iii) Calculate electric field V at a distance of 5 cm from centre of sphere A.

A metal sphere of radius 10 cm is charged to a high voltage. If this metal sphere is mounted on a wooden block, then charge will reside on its surface and will not flow from it. As we know dielectric strength of air is 3 x 10⁶ V m^-1, then the surrounding air will start conducting and charge stored on the isolated sphere will be lost.
(i) Explain why air will start conducting if electric field exceeds dielectric strength?
(ii) Calculate the maximum charge this sphere can hold.
(iii) Why sometimes electric charge is leaked before the above value of potential is reached.