12th Standard CBSE Maths Subjects Question Paper Software Subscription
QB365 covers complete information about 12th Standard CBSE Maths Subject for 2024-2025 Exam. Question Bank includes 12th Standard CBSE Maths Subjects Book back, exercise, Updated Question types MCQ, Case Study , Assertion and reason with solution, Previous year asked questions, all possible questions and other key points also. All question with detailed answers are readily available for preparting Maths question papers.
All Chapters Covered

Create Unlimited Question Papers

Access anywhere anytime

Multiple Pattern Question Papers
Share your Question Paper

Font size, line spacing, watermark etc,
Our Other Subjects for 12th Standard CBSE
12th Standard CBSE Maths Chapters / Lessons
Relations and Functions
Inverse Trigonometric Functions
Matrices
Determinants
Continuity and Differentiability
Applications of Derivatives
Integrals
Applications of the Integrals
Differential Equations
Vector Algebra
Three - Dimensional Geometry
Linear Programming
Probability
12th Standard CBSE Maths Chapters / Lessons Syllabus
Relations and Functions
1. Relations and Functions
Types of relations: reflexive, symmetric, transitive and equivalence relations. One to one and onto functions, composite functions, inverse of a function. Binary operations.
2. Inverse Trigonometric Functions
Definition, range, domain, principal value branch. Graphs of inverse trigonometric functions. Elementary properties of inverse trigonometric functions.
Algebra
1. Matrices
Concept, notation, order, equality, types of matrices, zero and identity matrix, transpose of a matrix, symmetric and skew symmetric matrices. Operation on matrices: Addition and multiplication and multiplication with a scalar. Simple properties of addition, multiplication and scalar multiplication. Noncommutativity of multiplication of matrices and existence of non-zero matrices whose product is the zero matrix (restrict to square matrices of order 2).Concept of elementary row and column operations. Invertible matrices and proof of the uniqueness of inverse, if it exists; (Here all matrices will have real entries).
2. Determinants
Determinant of a square matrix (up to 3 x 3 matrices), properties of determinants, minors, co-factors and applications of determinants in finding the area of a triangle. Adjoint and inverse of a square matrix. Consistency, inconsistency and number of solutions of system of linear equations by examples, solving system of linear equations in two or three variables (having unique solution) using inverse of a matrix.
Calculus
1. Continuity and Differentiability
Continuity and differentiability, derivative of composite functions, chain rule, derivatives of inverse trigonometric functions, derivative of implicit functions. Concept of exponential and logarithmic functions.
Derivatives of logarithmic and exponential functions. Logarithmic differentiation, derivative of functions expressed in parametric forms. Second order derivatives. Rolle's and Lagrange's Mean Value Theorems (without proof) and their geometric interpretation.
2. Applications of Derivatives
Applications of derivatives: rate of change of bodies, increasing/decreasing functions, tangents and normals, use of derivatives in approximation, maxima and minima (first derivative test motivated geometrically and second derivative test given as a provable tool). Simple problems (that illustrate basic principles and understanding of the subject as well as real-life situations).
3. Integrals
Integration as inverse process of differentiation.Integration of a variety of functions by substitution, by partial fractions and by parts, Evaluation of simple integrals of the following types and problems based on them.
\(\int { \frac { dx }{ { x }^{ 2 }\pm { a }^{ 2 } } \int { \frac { dx }{ \sqrt { { x }^{ 2 }\pm { a }^{ 2 } } } } \int { \frac { dx }{ \sqrt { { a }^{ 2 }-{ x }^{ 2 } } } } } ,\int { \frac { dx }{ { ax }^{ 2 }+bx+c } } ,\int { \frac { dx }{ \sqrt { { ax }^{ 2 }+bx+c } } } \)
\(\int { \frac { px+q }{ { ax }^{ 2 }+bx+c } } dx,\int { \frac { px+q }{ \sqrt { { ax }^{ 2 }+bx+c } } } dx,\int { \sqrt { { a }^{ 2 }\pm { x }^{ 2 } } } dx,\sqrt { { x }^{ 2 }-{ a }^{ 2 } } dx\)
\(\int { \sqrt { { ax }^{ 2 }+bx+c } } dx,\int { (px+q) } \sqrt { { ax }^{ 2 }+bx+c } dx\)
Definite integrals as a limit of a sum, Fundamental Theorem of Calculus (without proof).Basic properties of definite integrals and evaluation of definite integrals.
4. Applications of the Integrals
Applications in finding the area under simple curves, especially lines, circles/parabolas/ellipses (in standard form only), Area between any of the two above said curves (the region should be clearly identifiable).
5. Differential Equations
Definition, order and degree, general and particular solutions of a differential equation.Formation of differential equation whose general solution is given.Solution of differential equations by method of separation of variables solutions of homogeneous differential equations of first order and first degree. Solutions of linear differential equation of the type
Vectors and Three-Dimensional Geometry
1. Vectors
Vectors and scalars, magnitude and direction of a vector.Direction cosines and direction ratios of a vector. Types of vectors (equal, unit, zero, parallel and collinear vectors), position vector of a point, negative of a vector, components of a vector, addition of vectors, multiplication of a vector by a scalar, position vector of a point dividing a line segment in a given ratio. Definition, Geometrical Interpretation, properties and application of scalar (dot) product of vectors, vector (cross) product of vectors, scalar triple product of vectors.
2. Three - dimensional Geometry
Direction cosines and direction ratios of a line joining two points.Cartesian equation and vector equation of a line, coplanar and skew lines, shortest distance between two lines.Cartesian and vector equation of a plane.Angle between (i) two lines, (ii) two planes, (iii) a line and a plane.Distance of a point from a plane.
Linear Programming
1. Linear Programming
introduction, related terminology such as constraints, objective function, optimization, different types of linear programming (L.P.) problems, mathematical formulation of L.P. problems, graphical method of solution for problems in two variables, feasible and infeasible regions(bounded or unbounded), feasible and infeasible solutions, optimal feasible solutions (up to three non-trivial constraints).
Probability
1. Probability
Conditional probability, multiplication theorem on probability, independent events, total probability, Bayes’ theorem, Random variable and its probability distribution, mean and variance of random variable. Repeated independent (Bernoulli) trials and Binomial distribution.
Relations and Functions
Introduction-Types of Relations-Types of Functions-Composition of Functions and Invertible Function-Binary Operations
Inverse Trigonometric Functions
Introduction-Basic Concepts-Properties of Inverse Trigonometric Functions
Matrices
Introduction-Matrix-Types of Matrices-Operations on Matrices-Transpose of a Matrix-Symmetric and Skew-SymmetricMatrices-Elementary Operation Transformation of a Matrix-Invertible Matrices
Determinants
Introduction-Determinant-Properties of Determinants-Area of a Triangle-Minors and Cofactors-Adjoint and Inverse of a Matrix-Applications of Determinants and Matrices
Continuity and Differentiability
Introduction-Continuity-Differentiability-Exponential and Logarithmic Functions-Logarithmic Differentiation-Derivatives of Functions in Parametric Forms-Second Order Derivative-Mean Value Theorem
Application of Derivatives
Introduction-Rate of Change of Quantities-Increasing and Decreasing Functions-Tangents and Normals-Approximations-Maxima and Minima
Integrals
Introduction-Integration as an Inverse Process of Differentiation-Methods of Integration-Integrals of some Particular Functions-Integration by Partial Fractions-Integration by Parts-Definite Integral-Fundamental Theorem of Calculus-Evaluation of Definite Integrals by Substitution-Some Properties of Definite Integrals
Application of Integrals
Introduction-Area under Simple Curves-Area between Two Curves
Differential Equations
Introduction-Basic Concepts-General and Particular Solutions of a Differential Equation-Formation of a Differential Equation whose General Solution is given-Methods of Solving First order, First Degree Differential Equations
Vector Algebra
Introduction-Some Basic Concepts-Types of Vectors-Addition of Vectors-Multiplication of a Vector by a Scalar-Product of Two Vectors
Three Dimensional Geometry
Introduction-Direction Cosines and Direction Ratios of a Line-Equation of a Line in Space-Angle between Two Lines-Shortest Distance between Two Lines-Plane-Coplanarity of Two Lines-Angle between Two Planes-Distance of a Point from a Plane-Angle between a Line and a Plane
Linear Programming
Introduction-Linear Programming Problem and its Mathematical Formulation-Different Types of Linear Programming Problems
Probability
Introduction-Conditional Probability-Multiplication Theorem on Probability-Independent Events-Baye’s Theorem-Random Variables and its Probability Distributions-Bernoulli Trials and Binomial Distribution
Features in Question Paper Preparation software

(or) type Question

Add or Remover

Sub Questions

Adding Notes

Multiple Pattern

All subjects available
How to Create 12th Standard CBSE Maths Question Paper
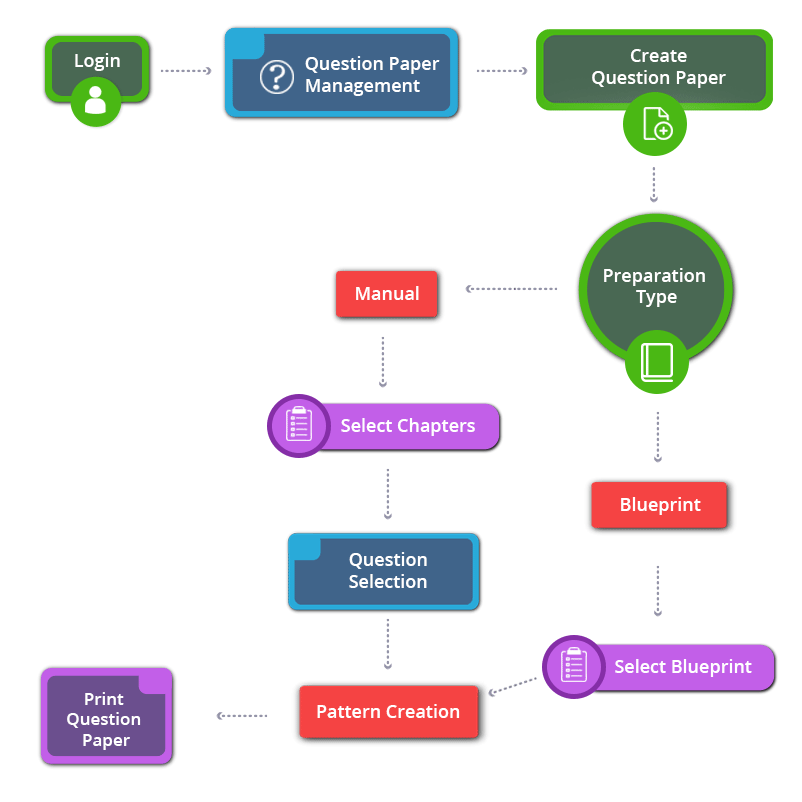

12th Standard CBSE Maths
- Covers all chapters
- Unique Creative Questions
- Unlimited Question Paper
- Multiple Patterns & Answer keys
0


