9th Standard CBSE Mathematics Subjects Question Paper Software Subscription
QB365 covers complete information about 9th Standard CBSE Mathematics Subject for 2024-2025 Exam. Question Bank includes 9th Standard CBSE Mathematics Subjects Book back, exercise, Updated Question types MCQ, Case Study , Assertion and reason with solution, Previous year asked questions, all possible questions and other key points also. All question with detailed answers are readily available for preparting Maths question papers.
All Chapters Covered

Create Unlimited Question Papers

Access anywhere anytime

Multiple Pattern Question Papers
Share your Question Paper

Font size, line spacing, watermark etc,
Our Other Subjects for 9th Standard CBSE
9th Standard CBSE Mathematics Chapters / Lessons
Number Systems
Polynomials
Coordinate Geometry
Linear Equations in Two Variables
Introduction to Euclid's Geometry
Lines and Angles
Triangles
Quadrilaterals
Areas of Parallelograms and Triangles
Circles
Constructions
Heron's Formula
Surface Areas and Volumes
Statistics
Probability
9th Standard CBSE Mathematics Chapters / Lessons Syllabus
NUMBER SYSTEMS
REAL NUMBERS
Review of representation of natural numbers, integers, rational numbers on the number line. Representation of terminating / non-terminating recurring decimals on the number line through successive magnification. Rational numbers as recurring/ terminating decimals. Operations on real numbers. Examples of non- ecurring/non-terminating decimals. Existence of non-rational numbers (irrational numbers) such as 2, 3 and their representation on the number line. Explaining that every real number is represented by a unique point on the number line and conversely, viz. every point on the number line represents a unique real number. Definition of nth root of a real number. Existence of x for a given positive real number x and its representation on the number line with geometric proof. Rationalization (with precise meaning) of real numbers of the type (%)(and their combinations) where x and y are natural number and a and b are integers - Recall of laws of exponents with integral powers. Rational exponents with positive real bases (to be done by particular cases, allowing learner to arrive at the general laws.)
ALGEBRA
POLYNOMIALS
Definition of a polynomial in one variable, with examples and counter examples. Coefficients of a polynomial, terms of a polynomial and zero polynomial. Degree of a polynomial. Constant, linear, quadratic and cubic polynomials. Monomials, binomials, trinomials. Factors and multiples. Zeros of a polynomial. Motivate and State the Remainder Theorem with examples. Statement and proof of the Factor Theorem. Factorization of ax2 + bx + c, a ≠ 0 where a, b and c are real numbers, and of cubic polynomials using the Factor Theorem.
Recall of algebraic expressions and identities. Verification of identities:
(x+y+z)2 = x2 +y2 +z2 +2xy+2yz+2zx
(x±y)3 = x3 ±y3 ±3xy (x±y)
x3 ±y3 = (x±y) (x2 xy+y2 )
x3 +y3 +z3 -3xyz=(x+y+z) (x2 +y2 +z2 -xy-yz-zx) and their use in factorization of polynomials.
LINEAR EQUATIONS IN TWO VARIABLES
Recall of linear equations in one variable. Introduction to the equation in two variables. Focus on linear equations of the type ax+by+c=0. Prove that a linear equation in two variables has infinitely many solutions and justify their being written as ordered pairs of real numbers, plotting them and showing that they lie on a line. Graph of linear equations in two variables. Examples, problems from real life, including problems on Ratio and Proportion and with algebraic and graphical solutions being done simultaneously.
COORDINATE GEOMETRY
The Cartesian plane, coordinates of a point, names and terms associated with the coordinate plane, notations, plotting points in the plane
GEOMETRY
INTRODUCTION TO EUCLID’S GEOMETRY
History - Geometry in India and Euclid’s geometry. Euclid’s method of formalizing observed phenomenon into rigorous Mathematics with definitions, common/ obvious notions, axioms/postulates and theorems. The five postulates of Euclid. Equivalent versions of the fifth postulate. Showing the relationship between axiom and theorem, for example:
(Axiom) 1. Given two distinct points, there exists one and only one line through them.
(Theorem) 2. (Prove) Two distinct lines cannot have more than one point in common.
LINES AND ANGLES
(Motivate) If a ray stands on a line, then the sum of the two adjacent angles so formed is 1800 and the converse.
(Prove) If two lines intersect, vertically opposite angles are equal.
(Motivate) Results on corresponding angles, alternate angles, interior angles when a transversal intersects two parallel lines.
(Motivate) Lines which are parallel to a given line are parallel.
(Prove) The sum of the angles of a triangle is 1800.
TRIANGLES
(Motivate) Two triangles are congruent if any two sides and the included angle of one triangle is equal to any two sides and the included angle of the other triangle (SAS Congruence).
(Prove) Two triangles are congruent if any two angles and the included side of one triangle is equal to any two angles and the included side of the other triangle (ASA Congruence).
(Motivate) Two triangles are congruent if the three sides of one triangle are equal to three sides of the other triangle (SSS Congruence).
(Motivate) Two right triangles are congruent if the hypotenuse and a side of one triangle are equal (respectively) to the hypotenuse and a side of the other triangle. (RHS Congruence)
(Prove) The angles opposite to equal sides of a triangle are equal.
(Motivate) The sides opposite to equal angles of a triangle are equal.
(Motivate) Triangle inequalities and relation between ‘angle and facing side’ inequalities in triangles.
QUADRILATERALS
(Prove) The diagonal divides a parallelogram into two congruent triangles.
(Motivate) In a parallelogram opposite sides are equal, and conversely
(Motivate) In a parallelogram opposite angles are equal, and conversely.
(Motivate) A quadrilateral is a parallelogram if a pair of its opposite sides is parallel and equal.
(Motivate) In a parallelogram, the diagonals bisect each other and conversely.
(Motivate) In a triangle, the line segment joining the mid points of any two sides is parallel to the third side and in half of it and (motivate) its converse.
AREA
Review concept of area, recall area of a rectangle.
(Prove) Parallelograms on the same base and between the same parallels have the same area.
(Motivate) Triangles on the same (or equal base) base and between the same parallels are equal in area.
CIRCLE
Through examples, arrive at definition of circle and related concepts-radius, circumference, diameter, chord, arc, secant, sector, segment, subtended angle.
(Prove) Equal chords of a circle subtend equal angles at the center and (motivate) its converse.
(Motivate) The perpendicular from the center of a circle to a chord bisects the chord and conversely, the line drawn through the center of a circle to bisect a chord is perpendicular to the chord.
(Motivate) There is one and only one circle passing through three given noncollinear points.
(Motivate) Equal chords of a circle (or of congruent circles) are equidistant from the center (or their respective centers) and conversely.
(Prove) The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
(Motivate) Angles in the same segment of a circle are equal.
(Motivate) If a line segment joining two points subtends equal angle at two other points lying on the same side of the line containing the segment, the four points lie on a circle.
(Motivate) The sum of either of the pair of the opposite angles of a cyclic quadrilateral is 180o and its converse.
CONSTRUCTIONS
Construction of bisectors of line segments and angles of measure 60o , 90o , 45o etc., equilateral triangles.
Construction of a triangle given its base, sum/difference of the other two sides and one base angle.
Construction of a triangle of given perimeter and base angles.
MENSURATION
AREAS
Area of a triangle using Heron’s formula (without proof) and its application in finding the area of a quadrilateral.
SURFACE AREAS AND VOLUMES
Surface areas and volumes of cubes, cuboids, spheres (including hemispheres) and right circular cylinders/cones.
STATISTICS & PROBABILITY
STATISTICS
Introduction to Statistics: Collection of data, presentation of data — tabular form, ungrouped / grouped, bar graphs, histograms (with varying base lengths), frequency polygons. Mean, median and mode of ungrouped data.
PROBABILITY
History, Repeated experiments and observed frequency approach to probability
Focus is on empirical probability. (A large amount of time to be devoted to group and to individual activities to motivate the concept; the experiments to be drawn from real - life situations, and from examples used in the chapter on statistics).
Number Systems
Introduction-Irrational Numbers-Real Numbers and their Decimal Expansions-Representing Real Numbers on the Number Line-Operations on Real Numbers-Laws of Exponents for Real Numbers
Polynomials
Introduction-Polynomials in One Variable-Zeroes of a Polynomial-Remainder Theorem-Factorisation of Polynomials-Algebraic Identities
Coordinate Geometry
Introduction-Cartesian System-Plotting a Point in the Plane if its Coordinates are Given
Linear Equations in Two Variables
Introduction-Linear Equations-Solution of a Linear Equation-Graph of a Linear Equation in Two Variables-Equations of Lines Parallel to the x-axis and y-axis
Introduction to Euclid’s Geometry
Introduction-Euclid’s Definitions, Axioms and Postulates-Equivalent Versions of Euclid’s Fifth Postulate
Lines and Angles
Introduction-Basic Terms and Definitions-Intersecting Lines and Non-intersecting Lines-Pairs of Angles-Parallel Lines and a Transversal-Lines Parallel to the Same Line-Angle Sum Property of a Triangle
Triangles
Introduction-Congruence of Triangles-Criteria for Congruence of Triangles-Some Properties of a Triangle-Some More Criteria for Congruence of Triangles-Inequalities in a Triangle
Quadrilaterals
Introduction-Angle Sum Property of a Quadrilateral-Types of Quadrilaterals-Properties of a Parallelogram-Another Condition for a Quadrilateral to be a Parallelogram-The Mid-point Theorem
Areas of Parallelograms and Triangles
Introduction-Figures on the Same Base and Between the Same Parallels-Parallelograms on the same Base and between the same Parallels-Triangles on the same Base and between the same Parallels
Circles
Introduction-Circles and Its Related Terms: A Review-Angle Subtended by a Chord at a Point-Perpendicular from the Centre to a Chord-Circle through Three Points-Equal Chords and Their Distances from the Centre-Angle Subtended by an Arc of a Circle-Cyclic Quadrilaterals
Constructions
Introduction-Basic Constructions-Some Constructions of Triangles
Heron’s Formula
Introduction-Area of a Triangle: by Heron’s Formula-Application of Heron’s Formula in Finding Areas of Quadrilaterals
Surface Areas and Volumes
Introduction-Surface Area of a Cuboid and a Cube-Surface Area of a Right Circular Cylinder-Surface Area of a Right Circular Cone-Surface Area of a Sphere-Volume of a Cuboid-Volume of a Cylinder-Volume of a Right Circular Cone-Volume of a Sphere
Statistics
Introduction-Collection of Data-Presentation of Data-Graphical Representation of Data-Measures of Central Tendency
Probability
Introduction-Probability-an Experimental Approach
Features in Question Paper Preparation software

(or) type Question

Add or Remover

Sub Questions

Adding Notes

Multiple Pattern

All subjects available
How to Create 9th Standard CBSE Mathematics Question Paper
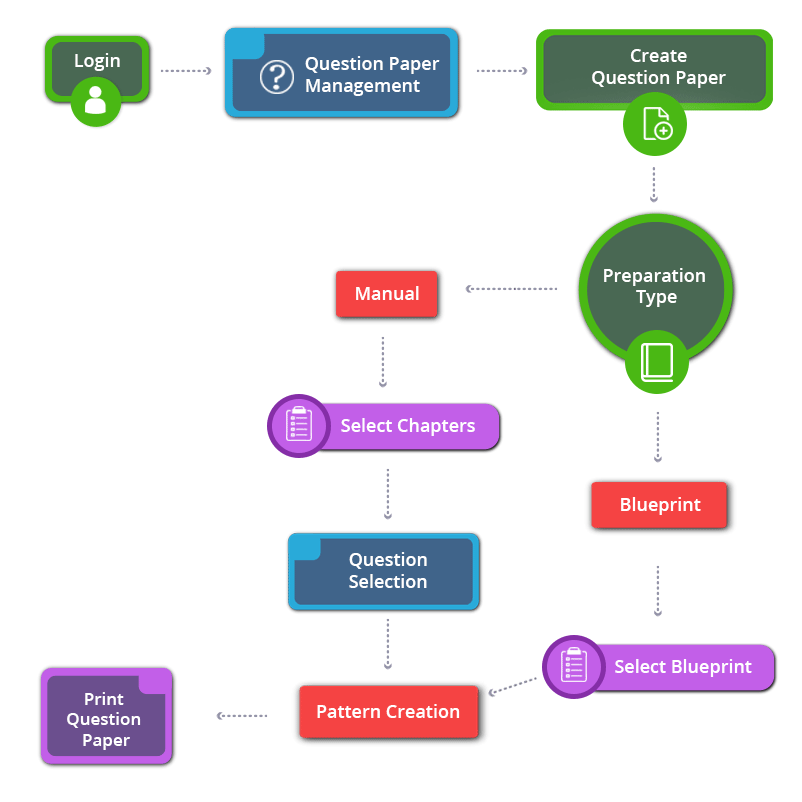

9th Standard CBSE Mathematics
- Covers all chapters
- Unique Creative Questions
- Unlimited Question Paper
- Multiple Patterns & Answer keys
0


