9th Standard CBSE Mathematics Public Exam Important Question 2019-2020
By QB365 on 29 Feb, 2020
9th Standard CBSE Mathematics Public Exam Important Question 2019-2020
linlaxinfotech
Important Question Part-III
9th Standard CBSE
-
Reg.No. :
Mathematics
-
If \(\sqrt { 3 } =1.732\) and \(\sqrt { 2 } =1.414\) , the value of \(\frac { 1 }{ \sqrt { 3 } -\sqrt { 2 } } \) is:
(a)0.318
(b)3.146
(c)1/3.146
(d)\(\sqrt { 1.732 } -\sqrt { 1.414 } \)
-
For what value of a, is the polynomial \(x^3+2x^2-3ax-8\) divisible by x-4?
(a)\(\frac{22}{3}\)
(b)\(\frac{11}{3}\)
(c)11
(d)3
-
The distance of the point (1,0) from O is:
(a)0
(b)1
(c)2
(d)None of these
-
Any point on the line y = 3x is of the form:
(a)(a, 3a)
(b)(3a, a)
(c)\(\left(a,{a\over3}\right)\)
(d)\(\left({a\over3},-a\right)\)
-
John Playfair was a
(a)french mathematician
(b)Scottish mathematician
(c)Indian mathematician
(d)Egyptian mathematician
-
We can draw two different lines in
(a)Only one way
(b)two different ways
(c)three different ways
(d)None of these
-
The symbol for correspondence is
(a)⟶
(b)⇔
(c)↔
(d)≡
-
ABCD is a rhombus such that \(\angle \)ABC=\(40°\) then \(\angle \)ADC is equal to
(a)40°
(b)45°
(c)50°
(d)20°
-
In given figure, ABCD is a parallelogram. If ar(\(\Delta\)BFC) = 40 cm2, then ar(\(\Delta\) AEB) is equal to:
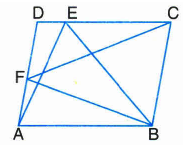 (a)
(a)20 cm2
(b)40 cm2
(c)80 cm2
(d)10 cm2
-
A and B are points on the circle with centre O. If a chord CD of the circle subtends an angle of 50° at the point A on the circle and \(\angle BDC=70°\), then \(\angle BCD\) equals:
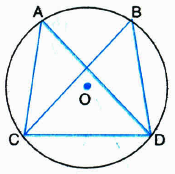 (a)
(a)60°
(b)50°
(c)70°
(d)90°
-
The sides of a triangular park are in the ratio 25: 17: 12 and its perimeter is 540 m. Find the smallest side of the park.
(a)60 m
(b)120 m
(c)90 m
(d)45 m
-
The lateral surface area of a cuboid of length l, breadth b and height h is
(a)2(lb + bh + hl)
(b)2(l + b)h
(c)lbh
(d)none of these.
-
The mean of 3,4,5,6,7 is
(a)7
(b)6
(c)5
(d)4
-
An experiment has two outcomes E and F P(E)+P(F) is equal to:
(a)1
(b)0
(c)2
(d)\(\frac { 1 }{ 2 } \)
-
Find the rational numbers a and b such that \(\frac { 2+5\sqrt { 7 } }{ 2-5\sqrt { 7 } } =a+\sqrt { 7 } b\)
(a) -
Write \((3a+4b+5c)^2\) in expanded form.
(a) -
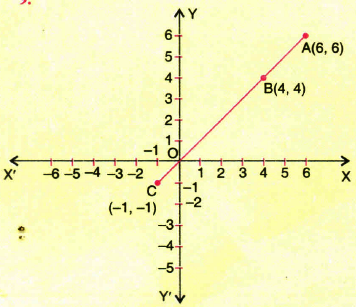
Plot the points A(6,6), B(4,4), C(-1,-1) in the Cartesian plane and show that the points are collinear.
(a) -
Solve 4x - 7 = 9. Represent the solution
(i) on the number line
(ii) in the Cartesian plane.(a) -
In a triangle PQR, X and Y are the points on PQ are QR respectively. If PQ = QR and QX = QY, Show that PX = RY.
(a) -
In figure if AB||CD||EF and x:y=3:2. Find z
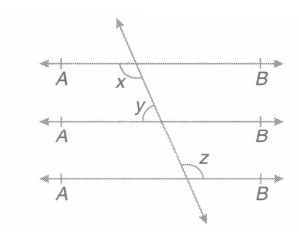 (a)
(a) -
D is any point on side BC of ΔABC, such that AD = AC. Show that AB > AD.
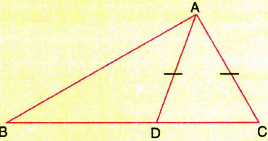 (a)
(a) -
Two parallel lines I and m are intersected by a transversal ' t'.Show that the quadrilateral formed by bisectors of interior angles is a rectangle.
(a) -
In the figure, the vertex A of \(\Delta \) ABC is joined to a point D on the side BC. The mid-point of AD is E. Prove that ar(\(\Delta \) BEC) =\(\frac { 1 }{ 2 } ar(\Delta ABC)\)
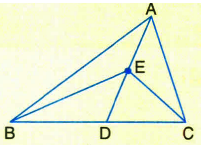 (a)
(a) -
PQRS is a cyclic quadrilateral, in which \(\angle P=2x°\), \(\angle Q=y°\), \(\angle R=3x°\) and \(\angle S=2y°\). Find the values of x and y.
(a) -
Construct a triangle of sides 3 cm, 3.5 cm and 5 cm. Bisect the smallest angle of the triangle.
(a) -
Find the area of the triangle whose two sides are of measure 13 cm and 14 cm and perimeter is 42 cm.
(a) -
The pillars of a temple are cylindrically shaped. If each pillar has a circular base of radius 20 cm and height 10 m, how much concrete mixture would be required to build 14 such pillars?
(a) -
A family with monthly income of Rs 20,000 had planned the following expenditures per month under various heads:
Heads
Expenditure (in Rs 1000) Grocery 4 Rent 5 Education of children 5 Medicine 2 Fuel 2 Entertainment 1 Miscellaneous 1 Draw a graph for the data above.
(a) -
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes
Outcome Frequency 3 heads 24 2 heads 70 1 head 75 3 tails 31 Compute the probability of getting
(i) less than 2 heads
(ii) 3 heads.(a) -
If a = 2 + √5 and b = \(\frac{1}{a}\), find a2 + b2
(a) -
Write the degree of the following polynomials:
5x3 + 4x2 + 7x(a) -
Find the coordinates of the vertices of a rectangle placed in III quadrant, in the Cartesian plane with length 'p' units on x-axis and breadth 'q' units on y-axis.
(a) -
Write four solutions for each of the following equations:
x=4y(a) -
In the given figure, if \(\angle1=\angle3, \angle2=\angle4\ and\ \angle3=\angle4\), write the relation between \(\angle1\ and\ \angle2\) using Euclid's axiom.
(a) -
In the given figure, \(PO\bot AB\), If x:y:z=1:3:5, then find the degree measure of x,y and z.
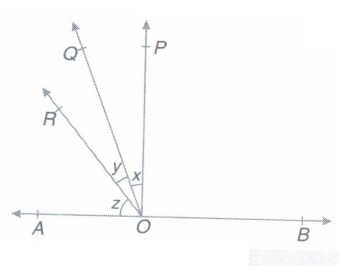 (a)
(a) -
Show that of all line segments drawn from a given point not on it, the perpendicular line segment is the shortest.
(a) -
ABCD is a parallelogram. P and Q are points on DC and AB respectively, such that \(\angle DAP=\angle BCQ\) .Show that AQCP is a parallelogram.
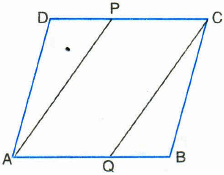 (a)
(a) -
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
(a) -
Draw AB = 6 cm. Construct an angle of \(30°\) at A and also draw the perpendicular bisector of AB.
(a) -
A kite in the shape of a square with a diagonal 32 cm and an isosceles triangle of base 8 cm and side 6cm each is to be made of three different shades as shown in figure. How much paper of each shade has been used in it?
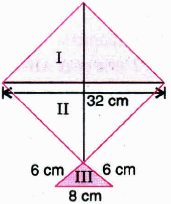 (a)
(a) -
If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find
(i) radius of its base
(ii) its volume.(a) -
The length of 40 leaves of a plant are measured a correct one millimeter, and the obtained data is represented in the following table:
Length (in mm) Number of leaves 118-126 3 127-135 5 136-144 9 145-153 12 154-162 5 163-171 4 172-180 2 (i) Draw a histogram to represent the given data.
(ii) Is there any suitable graphical representation for the same data?
(iii) Is it correct to conclude that the maximum number of leaves are 153 mm long? Why?(a) -
Given below is the frequency distribution of salary in Rs of 80 workers in a factory.
Salary No.of workers 1000-2000 8 2000-3000 14 3000-4000 20 4000-5000 24 5000-6000 14 Find the probability that the salary of a worker selected at random is:
(i) Less than 4000
(ii) More than or equal to 3000
(iii) More than or equal to 2000 but less than 5000(a) -
Prove that \(\frac { 1 }{ 3+\sqrt { 7 } } +\frac { 1 }{ \sqrt { 7 } +\sqrt { 5 } } +\frac { 1 }{ \sqrt { 5 } +\sqrt { 3 } } +\frac { 1 }{ \sqrt { 3 } +1 } =1\)
(a) -
State Factor theorem. Using Factor theorem, factorise x3-3x2-x+3.
(a) -
Plot the points A(3,0), B(3,3) and C(0,3) in a Cartesian plane.Join OA, OB, BC and CO.Name the figure so formed and write its one property.
(a) -
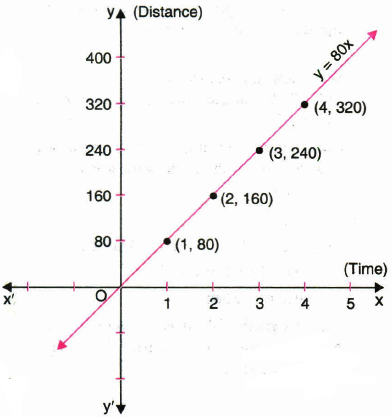
Rohit is driving his car at a uniform speed of 80 km per hour. Draw time-distance graph taking time along x-axis and distance along y-axis.
(a) -
In the given figure AB = BC and BX = BY. Show that AX = CY. State Euclid's Axiom used.
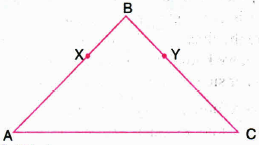 (a)
(a) -
If l,m,n are three lines such that l || m and n \(\bot \) l , then prove that n \(\bot \)m
(a) -
In \(\triangle\)ABC and \(\triangle\)PQR, AB = PQ, AC = PR and altitude AM and PN are equal. Show that, \(\triangle ABC\cong \triangle PQR.\)
(a) -
Show that the bisectors of angles of a parallelogram form a rectangle
(a) -
PQRS and ABRS are parallelogram and X is any on side BR.Prove that
(i)area PQRS=are ABRS
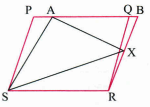
(ii)area AXS=\(1\over2\) area ABRS
(iii)are AXS=\(1\over2\) area PQRS
(iv)Itwari comments that if X is the mid-point of BR, then area ABX = area SXR.Is he correct?Which value is depicted by his comments?
(iv)Write the formulae used in the solution(a) -
In the figure, diameter AB and a chord AC have a 'common end point A. If the length of AB is 20 cm and of AC is 12 cm, how far is AC from the centre of the circle?
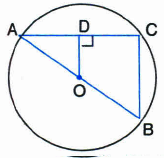 (a)
(a) -
(i)Construct a triangle XYZ in which \(\angle\)Y = 30°, \(\angle\)Z = 90° and XY + YZ + ZX = 11cm
(ii) Measure \(\angle\)XYZ
(iii)Measure \(\angle\)XZY
(iv)Measure XY
(v)Measure YZ
(vi)Measure Zx
(vii)Is XY+YZ+ZX=11cm?
(viii)Apala says that\(\angle\)YXZ=600.Is she right?which value is depicted by her statement?(a) -
The base of an isosceles triangle measures 24 cm and its area is 60 cm2, Find its perimeter.
(a) -
The diameter of a cylindrical roller 120cm long is 84cm.It takes 500 complete resolution to level a playground.Find
(i)radius of roller
(ii)curved surface area
(iii)area of the playground levelled in one revoluation
(iv)area of the playground levelled in 500 revolution
(v)cost of levelling at TRs.7.50 per sq.m
(vi)Apala is confident that the volume of the roller is 665280 cm3.Is Apala correct?Which value is depicted by her confidence?
(vii)write the formulae used in the solution(a) -
The following table gives the pocket money (in Rs) given to children per day by their Parents:
Pocket
Money0-10 10-20 20-30 30-40 40-50 No. of children 12 23 35 20 10 Represent the data in the form of a historgram
(a) -
The percentages of marks obtained by a student in examination are given below:
Examination
subjects% marks I 58 II 64 III 76 IV 62 V 85 Find the probability that the student gets
(i) a first class i.e. at least 60% marks
(ii) a distinction i.e. 75% or above
(iii) marks between 70% and 80%(a) -
If x = 3-2√2, find the value of √x+\(\frac{1}{\sqrt{x}}\)
(a) -
For spreading the message "Save Girl Child Save Future" a rally was organized by some students of a school. They were given triangular cardboard piece PQR which they divided in to two parts by drawing the angle bisectors QO and RO of base angles Q and R and wrote a slogan. Prove that \(\angle\)QOR = 90° + \(\frac{1}{2}\)\(\angle\)P. What is the benefit of these types of rallies?
(a) -
In the given figure ABCD is a parallelogram and E is the mid-point of AD. A line through D, drawn parallel to EB, meets AB produced at F and BC at L Prove that
(i) AF = 2DC
(ii) DF = 2DL
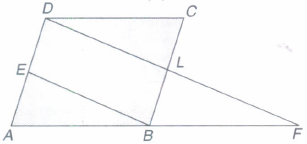 (a)
(a) -
Three students Priyanka, Sania and David are protesting against killing innocent animals for commercial purposes in a circular park of radius 20 m. They are standing at equal distance on its boundary by holding banners in their hands.
(i) Find the distance between each of them?
(ii) Which mathematical concept is used in it?
(iii) How does an act like this reflects their attitude towards society?(a) -
Two solid spheres made of the same metal have masses 5920 g of and 740 g respectively. Determine the radius of the larger sphere, if the diameter of the smaller sphere is 5 cm.
(a) -
Represent the following data by means of a frequency polygon.
Marks Frequency 41-45 4 45-49 10 49-53 15 53-57 18 57-61 20 61-65 12 65-69 13 (a)
Section - A
Section - B
Section - C
Section - D
Section - E
*****************************************
Important Question Part-III Answer Keys
-
(b)
3.146
-
(a)
\(\frac{22}{3}\)
-
(b)
1
-
(a)
(a, 3a)
-
(b)
Scottish mathematician
-
(b)
two different ways
-
(c)
↔
-
(a)
40°
-
(b)
40 cm2
-
(a)
60°
-
(d)
45 m
-
(b)
2(l + b)h
-
(c)
5
-
(a)
1
-
\(\quad a=-\frac { 179 }{ 171 } ,b=\frac { -20 }{ 171 } \)
-
Comparing the given expression with (x + y + z)2, we find that
x = 3a, y = 4b and z = 5c.
Therefore, using Identity V, we have
(3a + 4b + 5c)2 = (3a)2 + (4b)2 + (5c)2 + 2(3a)(4b) + 2(4b)(5c) + 2(5c)(3a)
= 9a2 + 16b2 + 25c2 + 24ab + 40bc + 30ac -
-
x=4
-
PQ = QR
QX = QY
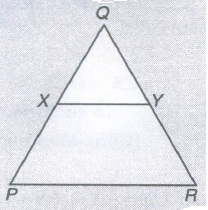
If equals are subtracted from equals, the remainders are also equal.
We have PQ - QX = QR - QY
PX = RY -
Let x=3k, y=2k
Then, x+y=3k+2k=180o
(Angles on the same side of transversal)
5k=180o
k=360
x=3k=108o
y=2k=72o
Thus, \(\angle z=\angle x=108^o\) (Alternate interior angles) -
-
∠APR=ㄥDRP
or ㄥ1=ㄥ2
But these are alternate interior angles
SP II RQ, SR II PQ
PQRS is a parallelogram
∠APR+ㄥBPR=180°,(linear pair)
⇒ \(\frac{1}{2}\) ∠APR+\(\frac{1}{2}\)ㄥBPR=\(\frac{1}{2}\)x180°
⇒ ∠1+ㄥ3=90°
⇒ ∠SPQ=90°
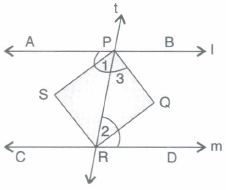
PQRS is a rectangle -
-
36, 60
-
-
84 cm2
-
17.6 m3
-
We draw the bar graph of this data in the following steps. Note that the unit in the second column is thousand rupees. So, ‘4’ against ‘grocery’ means Rs. 4000.
1. We represent the Heads (variable) on the horizontal axis choosing any scale, since the width of the bar is not important. But for clarity, we take equal widths for all bars and maintain equal gaps in between. Let one Head be represented by one unit.
2. We represent the expenditure (value) on the vertical axis. Since the maximum expenditure is Rs. 5000, we can choose the scale as 1 unit = Rs.1000.
3. To represent our first Head, i.e., grocery, we draw a rectangular bar with width 1 unit and height 4 units.
4. Similarly, other Heads are represented leaving a gap of 1 unit in between two consecutive bars.
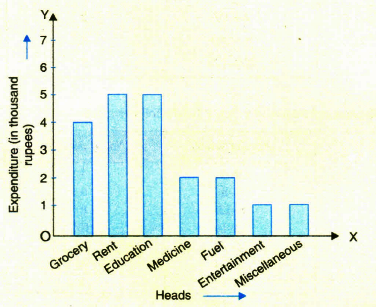
-
\((i)\frac { 53 }{ 100 }\)
\((ii)\frac { 3 }{ 25 } \) -
\(b=\frac { 1 }{ 2+\sqrt { 5 } } \)
\(=\frac { 1 }{ 2+\sqrt { 5 } } \times \frac { 2-\sqrt { 5 } }{ 2-\sqrt { 5 } } \)
\(=\frac { 2-\sqrt { 5 } }{ -1 } =-2+\sqrt { 5 } \)
\({ a }^{ 2 }={ \left( 2+\sqrt { 5 } \right) }^{ 2 }=9+4\sqrt { 5 } \)
\({ b }^{ 2 }={ \left( -2+\sqrt { 5 } \right) }^{ 2 }=9-4\sqrt { 5 } \)
\({ a }^{ 2 }+{ b }^{ 2 }=9+4\sqrt { 5 } +9-4\sqrt { 5 } \)
= 18 -
Term with the highest power of x = 5x3
Exponent of x in this term = 3
Therefore Degree of this polynomial = 3 -
(0,0); (-p,0); (5,0); (0,-q)
-
x=4y
\(\Rightarrow\ \ y={x\over 4}\)
Put x=0, we get \(y={0\over4}=0\)
Put x=4, we get \(y={4\over4}=1\)
Put x=-4, we get \(y={-4\over 4}=-1\)
Put x=2, we get \(y={2\over4}={1\over 2}\)
Four solutions are (0,0), (4, 1), (-4, -1) and \(\left(2,{1\over 2}\right)\) -
Here, \(\angle1=\angle3, \angle2=\angle4\ and\ \angle3=\angle4\), Euclid's first axiom says, the things which are equal to same things are equal to one another.
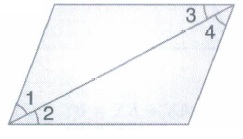
So, \(\angle 1=\angle 2\) -
\(OP\bot AB\)
\(\Rightarrow \angle POA=90^o\)
Let \(\angle POQ=a\)
\(\therefore \angle QOR=3a\)
\(\angle ROA=5a\)
\(\Rightarrow\) a+3a+5a=90o
\(\Rightarrow\) 9a=90o
\(\Rightarrow\)a=10o
\(\therefore\)x=10o
and y=3x10o=30o
z=5x10o=50o -
-
-
Construction: Join OA and OB.
∵ OA = OB = AB I Given
∴ \(\Delta AOB\) is equilateral.
∴ \(\angle AOB=60°\)
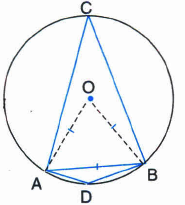
\(\angle ACB=\frac { 1 }{ 2 } \angle AOB\)
The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle
\(=\frac { 1 }{ 2 } \times 60°=30°\)
Now, ∵ ADBC is a cyclic quadrilateral.
∴ \(\angle ADB+\angle ACB=180°\)
The sum of either pair of opposite angles of a cyclic quadrilateral is 180°
\(\Rightarrow \ \angle ADB+30°=180°\)
\(\\ \Rightarrow \angle ADB=180°-30°\)
\(\\ \Rightarrow angle ADB=150°.\) -
-
Area of paper of shade I \(2\times \left( \frac { 1 }{ 2 } \times 16\times 16 \right) =256\)cm2
Similarly, Area of paper of shade II = 256 cm2
For area of paper of shade III
a = 8 cm, b = 6 cm, c = 6cm
\(\therefore s=\frac { a+b+c }{ 2 } =\frac { 8+6+6 }{ 2 } =10\) cm
\(\therefore \) Area of paper of shade III = \(\sqrt { s(s-a)(s-b)(s-c) } \)
\(=\sqrt { 10(10-8)(10-6)(10-6) } \)
\(=\sqrt { (10)(2)(4)(4) } =8\sqrt { 5 } \)
= 17.89 cm2 -
Let the radius of the base of the cylinder be r cm.
= 5 cm
Lateral surface =94.2 cm2
\(\Rightarrow 2\pi rh=94.2\)
\(\Rightarrow 2\times 3.14 \times r\times 5=94.2\)
\(\Rightarrow r=\frac{94.2}{2\times3.14\times5}\)
\(\Rightarrow r=\frac{94.2}{31.4}\)
\(\Rightarrow r=3cm\)
(ii) r = 3cm, h = 5 cm
ஃ Volume of the cylinder =\(\pi r^2h\)
= 3.14 x (3)2 x 5 =141.3 cm3 -
Modified Continues Distribution
Length (in mm) Number of leaves 117.5-126.5 3 126.5-135.5 5 135.5-144.5 9 144.5-153.5 12 153.5-162.5 5 162.5-171.5 4 171.5-180.5 2 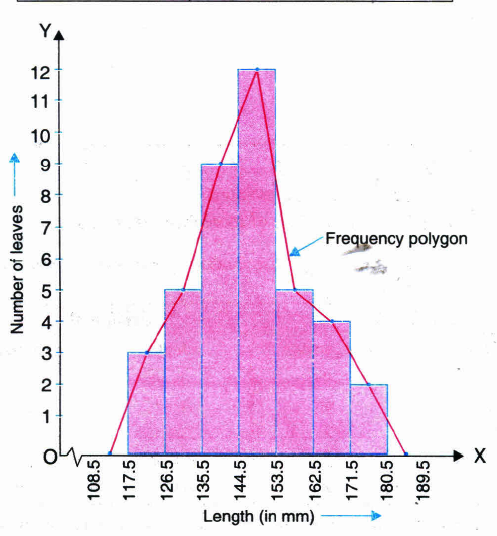
(ii) Frequency Polygon.
(iii) No, because the maximum number of leaves have their lengths lying in the original interval 145-153 (or modified interval 144.5-153.5). -
\((i)\frac { 21 }{ 40 }\)
\((ii)\frac { 29 }{ 40 }\)
\((iii)\frac { 29 }{ 40 } \) -
\(\frac { 1 }{ 3+\sqrt { 7 } } =\frac { 1 }{ 3+\sqrt { 7 } } \times \frac { 3-\sqrt { 7 } }{ 3-\sqrt { 7 } } =\frac { 3-\sqrt { 7 } }{ 9-7 } =\frac { 3-\sqrt { 7 } }{ 2 } \)
\(\frac { 1 }{ \sqrt { 7 } +\sqrt { 5 } } =\frac { 1 }{ \sqrt { 7 } +\sqrt { 5 } } \times \frac { \sqrt { 7 } -\sqrt { 5 } }{ \sqrt { 7 } -\sqrt { 5 } } =\frac { \sqrt { 7 } -\sqrt { 5 } }{ 2 } \)
\(\frac { 1 }{ \sqrt { 5 } +\sqrt { 3 } } =\frac { 1 }{ \sqrt { 5 } +\sqrt { 3 } } \times \frac { \sqrt { 5 } -\sqrt { 3 } }{ \sqrt { 5 } -\sqrt { 3 } } =\frac { \sqrt { 5 } -\sqrt { 3 } }{ 5-3 } \)
\(=\frac { \sqrt { 5 } -\sqrt { 3 } }{ 2 } \)
\(\frac { 1 }{ \sqrt { 3 } +1 } =\frac { 1 }{ \sqrt { 3 } +1 } \times \frac { \sqrt { 3 } -1 }{ \sqrt { 3 } -1 } =\frac { \sqrt { 3 } -1 }{ 3-1 } =\frac { \sqrt { 3 } -1 }{ 2 } \)
\(LHS=\frac { 3-\sqrt { 7 } }{ 2 } +\frac { \sqrt { 7 } -\sqrt { 5 } }{ 2 } +\frac { \sqrt { 5 } -\sqrt { 3 } }{ 2 } +\frac { \sqrt { 3 } -1 }{ 2 } \)
\(=\frac { 3-1 }{ 2 } =\frac { 2 }{ 2 } =1=RHS\) -
Factor theorem - statement
Let p(x)=x3-3x2-x+3
the factors of the constant term 3 are \(\pm \)1, \(\pm \)3
p(1)=13-3(1)2-1+3=0
(x-1) is a factor
p(-1)=(-1)3-3(-1)2-(-1)+3=0
(x+1) is a factor
p(3) = 33-3(3)2-3+3 = 0
(x-3) is a factor
(x-1)(x+1)(x-3) are the factors of p(x) -
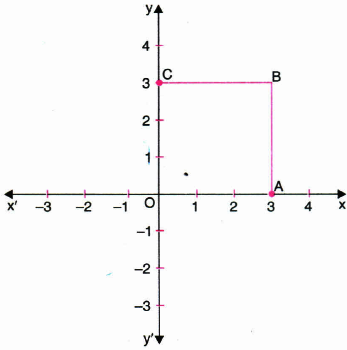
The figure formed is a square.
Its all the sides are of equal length. -
Let us represent time (in hour) by x and distance (in km) by y. Then, we have y =80x.
Table of solutionx 1 2 3 4 y 80 160 240 320 We plot the points (1, 80), (2, 160), (3, 240) and (4, 320) on a graph paper and join these points by a ruler to get the line which is the graph of the equation y = 80x.
-
We have
AB = BC
\(\Rightarrow \) AB - BX = BC - BX
|If equals are subtracted from equals, the remainders are equal (Euclid's Axiom (iii))
AB - BX = BC - BY \(|\)\( \because\) BX = BY
AB - BX coincides with AX;
BC - BY coincides with CY
[Things which coincide with one another are equal to one another (Euclid's Axiom (iv))] -
Given l,m,n are three lines such that l || m and n \(\bot \)m
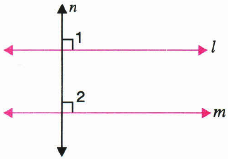
\(\therefore \)l || m and n is a transversal
\(\therefore \) \(\angle \)1=\(\angle \)2 |Corresponding angles
But \(\angle \)1=\(90^{ 0 }\)
\(\therefore \) \(\angle \) 2= \(90^{ 0 }\)
\(\Rightarrow \) n \(\bot \) m -
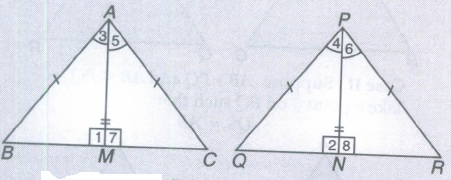
In \(\triangle\)AMB and \(\triangle\)PNQ,
AB = PQ (Given)
AM = PN (Given)
\(\angle\)1 = \(\angle\)2 = 90°
(AM\(\bot \)BC & PN \(\bot \)QR)
\(\Rightarrow\) \( \triangle AMP\cong \triangle PNQ\) (By RHS)
\(\Rightarrow\) \(\angle\)3 =\(\angle\)4 (By c.p.c.t.)
Similarly, \(\triangle AMC\cong \triangle PNR\)
\(\Rightarrow\) \(\angle\)5 = \(\angle\)6
(In congruent triangles, corresponding angles are equal)
\(\therefore\) In \(\triangle\)ABC and \(\triangle\)PQR,
AB = PQ (Given)
AC = PR (Given)
\(\angle\)A =\(\angle\)P
(\(\angle\)3 + \(\angle\)5 = \(\angle\)4 + \(\angle\)6) (proved)
\(\triangle ABC\cong \triangle PQR\) (By SAS) -
Let ABCD is a parallelogram
To show LMNO is a rectangle,
ㄥA+ㄥD=180°
\(\frac{1}{2}\)ㄥA+\(\frac{1}{2}\)ㄥD=90°
ㄥOAD+ㄥODA=90°
In ΔOAD,
ㄥOAD+ㄥADO+ㄥDOA=180°
⇒ ㄥDOA = 90°
⇒ ㄥLON = 90°
Similarly, ㄥOLM =ㄥLMN =ㄥMNO = 90°
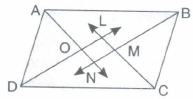
ஃ A quadrilateral with all angles 90° is a rectangle. Also opposite angles are equal. It is rectangle. -
-
Given: Diameter AB and a chord AC have a common end point A. AB = 20 cm and AC = 12 cm.
To determine: OD
Determination: ∵ OD丄AC
∴ \(AD=DC=\frac { 1 }{ 2 } AC=\frac { 1 }{ 2 } \times 12=6\quad cm\)
| ∵ The perpendicular drawn from the centre of a circle to a chord bisects the chord.
\(OA=OB=\frac { 1 }{ 2 } AB=\frac { 1 }{ 2 } \times 20=10\quad cm\)
In right triangle ODA,
OA2 = OD2 + AD2 I By Pythagoras Theorem
⇒ (10)2=OD2+(6)2
⇒ OD=8 cm
Hence, AC is 8 cm far from the centre of the circle. -
-
Area = \(=\frac { a }{ 4 } \sqrt { 4{ b }^{ 2 }-{ a }^{ 2 } } \)
\(\Rightarrow 60=\frac { 24 }{ 4 } \sqrt { 4{ b }^{ 2 }-{ (24) }^{ 2 } } \)
\(\Rightarrow 10=\sqrt { 4{ b }^{ 2 }-576 } \)
\(\Rightarrow 100=4{ b }^{ 2 }-576\) | Squaring
\(\Rightarrow 4{ b }^{ 2 }=676\)
\(\\ \Rightarrow { b }^{ 2 }=\frac { 676 }{ 4 } =169\)
\(\Rightarrow b=\sqrt { 169 } \) = 13 cm
\(\therefore\) Perimeter = a + b + b
= 24 + 13 + 13 = 50 cm -
-
Pocket Money No. of children 0-10 12 10-20 23 20-30 35 30-40 20 40-50 10 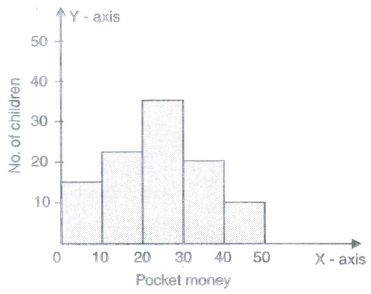
-
Total number of subjects = 5
(i) Number of subjects in which the student gets a first class = 4
Probability that the students gets a first class \(=\frac { 4 }{ 5 } \)
(ii) Number of subjects in which the student gets a distinction = 2
Probability that the student gets a distinction \(=\frac { 2 }{ 5 } \)
(iii) Number of subjects in which the student gets marks between 70% and 80% = 1
Probability that the students gets marks between 70% and 80% \(=\frac { 1 }{ 5 } \) -
\(x=3-2\sqrt { 2 } \Rightarrow \frac { 1 }{ x } =3+2\sqrt { 2 } \)
\({ \left( \sqrt { x } +\frac { 1 }{ \sqrt { x } } \right) }^{ 2 }=8\)
\(\Rightarrow \sqrt { x } +\frac { 1 }{ \sqrt { x } } =\pm 2\sqrt { 2 } \) -
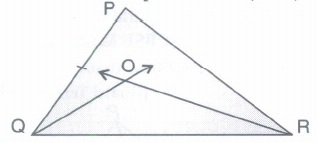
Proof: QO is bisector of \(\angle\)PQR
\(\angle\)OQR = \(\frac{1}{2}\)\(\angle\)PQR = \(\frac{1}{2}\) =\(\angle\)Q
RO is bisector \(\angle\)ORQ
\(\therefore\) \(\angle\)ORQ =\(\frac{1}{2}\) \(\angle\)PRQ = \(\frac{1}{2}\) \(\angle\)R
In \(\angle\)OQR
\(\angle\)QOR + \(\angle\)OQR + \(\angle\)ORQ = 180°
(Angle sum property)
\(\angle\)QOR + \(\frac{1}{2}\) \(\angle\)Q + \(\frac{1}{2}\) \(\angle\)R = 180°
\(\angle\)QOR = 180°- \(\frac{1}{2}\)(\(\angle\)Q + \(\angle\)R)
But in \(\angle\)PQR
\(\angle\)P + \(\angle\)Q + \(\angle\)R = 180°
\(\angle\)Q + \(\angle\)R = 180°- \(\angle\)P
\(\angle\)QOR = 180°- \(\frac{1}{2}\) (180°- \(\angle\)P)
= 180°-90° + \(\frac{1}{2}\)\(\angle\)P
= 90° + \(\angle\)P Hence Proved.
These type of rallies spread awareness among people for not to kill girl child and helping in equalising sex ratio. -
(i) As EB II DL and ED II BL.
Therefore EBLD is a parallelogram.
ஃ BL = ED
=\(\frac{1}{2}\)BC=CL ...(i)
Now in triangles DCL and FBL, we have
CL=BL from (i)
ㄥDLC= ㄥFLB
ㄥCDL=ㄥBFL
ΔCDL≡ΔBFL
CD= BF
and DL= FL
Now, BF = DC = AB
⇒ 2AB = 2DC
⇒ AF = 2DC
(ii) ∵ DL=FL
⇒ DF = 2DL -
(i) Let us assume that A, Band C are the position of Priyanka, Sania and David respectively on the boundary of circular park with centre O.
Draw AD\(\bot\) BC
Since the centre of the circle coincides with the centroid of the equilateral \(\triangle\) ABC
\(\therefore\) Radius of circumscribed circle = \(\frac{2}{3}\) AD
\(\Rightarrow 20=\frac { 2 }{ 3 } AD\)
\(\Rightarrow AD=20\times \frac { 2 }{ 3 } \)
\(\Rightarrow AD=30m\)
Now, AD\(\bot\)BC, and let AB=BC=CA=x
\(\Rightarrow BD=CD=\frac { 1 }{ 2 } BC=\frac { x }{ 2 } \)
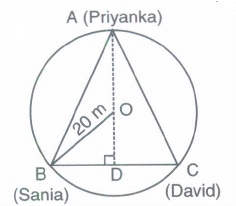
In rt. \(\triangle\)BDA, D=900
By Pythagoras Theorem, we have
AB2=BD2+AD2
\(\Rightarrow { x }^{ 2 }={ \left( \frac { x }{ 2 } \right) }^{ 2 }+{ (30) }^{ 2 }\)
\(\Rightarrow{ x }^{ 2 }-{ \frac { { x }^{ 2 } }{ 4 } }=90\)
\(\Rightarrow \frac { 3 }{ 4 } { x }^{ 2 }=90\)
\(\Rightarrow { x }^{ 2 }=900\times \frac { 4 }{ 3 } \)
\(\Rightarrow { x }^{ 2 }=1200\)
\(\therefore x=\sqrt { 1200 } =20\sqrt { 3 } \)
Hence, the distance between each of them is \(20\sqrt { 3 } .\)
(ii) Properties of the circle, equilateral triangle and Pythagoras theorem.
(iii) Live and let live. -
Let r and R be the radii of the smaller and larger spheres respectively, we have
\(r=\frac { 5 }{ 2 } cm\)
Volume of the smaller sphere \(=\frac { 4 }{ 3 } \pi { r }^{ 3 }=\frac { 4 }{ 3 } \pi { \left( \frac { 5 }{ 2 } \right) }^{ 3 }\)
\(=\frac { 4 }{ 3 } \times \pi \times \frac { 125 }{ 8 } { cm }^{ 3 }\)
Density of metal\(=\frac { mass }{ Valume } \)
\(=\frac { 740 }{ \frac { 4 }{ 3 } \pi \times \frac { 125 }{ 8 } } g\quad { cm }^{ 3 }\) ...........(i)
Volume of larger sphere = \(\frac { 4 }{ 3 } \pi { R }^{ 3 }\)
Density of metal=\(\frac { mass }{ Volume } =\frac { 5920 }{ \frac { 4 }{ 3 } \pi { R }^{ 3 } } \) ......(ii)
From (i) and (ii), we have
\(\frac { 740 }{ \frac { 4 }{ 3 } \pi \times \frac { 125 }{ 8 } } =\frac { 5920 }{ \frac { 4 }{ 3 } \pi { R }^{ 3 } } \)
\(\Rightarrow \quad { R }^{ 3 }=\frac { 5920\times 125 }{ 740\times 8 } \)
= 125
\(\Rightarrow\) R = 5 cm. -
Marks Frequency Class Marks 37-41 0 39 41-45 4 43 45-49 10 47 49-53 15 51 53-57 18 55 57-61 20 59 61-65 12 53 65-69 13 67 69-73 0 71 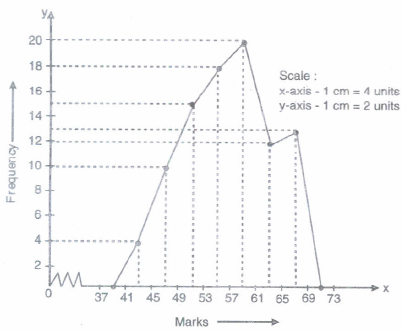
Section - A
Section - B
Section - C
Section - D
Section - E

























