9th Standard CBSE Mathematics Public Exam Sample Question 2020
By QB365 on 29 Feb, 2020
9th Standard CBSE Mathematics Public Exam Sample Question 2020
linlaxinfotech
Important Question Part-II
9th Standard CBSE
-
Reg.No. :
Mathematics
-
Which of the following is a rational number?
(a)\(1+\sqrt { 3 } \)
(b)\(\pi \)
(c)\(2\sqrt { 3 } \)
(d)0
-
If the polynomial p(x) is divided by (x+3), then the remainder will be:
(a)p(-1)
(b)p(2)
(c)p(-3)
(d)p(3)
-
If the points A(2,0), B(- 6,0) and C(3,a-3) lie on the x-axis, then the value of a is:
(a)0
(b)2
(c)3
(d)-6
-
The sum of the ages of Apala and Meenu is 48.Write a linear equation in two variables to represent the statement.
(a)x+y=48
(b)x-y-10=0
(c)2x+y=48
(d)x+2y=48
-
Pythagoras was a student of
(a)Thales
(b)Euclid
(c)both (a) and (b)
(d)Archimedes
-
Two angles measure \((30-a)^{ 0 }\) and \((125+2a)^{ 0 }\) If each one is the supplement of the other then the value of a is
(a)\(45^{ 0 }\)
(b)\(35^{ 0 }\)
(c)\(25^{ 0 }\)
(d)\(65^{ 0 }\)
-
If ΔABC is right angled at B, then:
(a)AB = AC
(b)AC < AB
(c)AB=BC
(d)AC > Ab
-
Find the measure of \(\angle \)AGF.
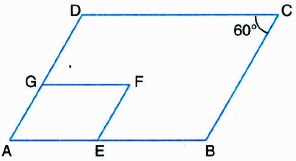 (a)
(a)60°
(b)120°
(c)30°
(d)90°
-
Which of the following figures donot lie between the same parallels?
(a) (b)
(b) (c)
(c) (d)
(d)
-
In the figure, O is the centre of the circle. Quadrilateral PQTS is a cyclic quadrilateral. If \(\angle POT=130°\) , then the measure of \(\angle x\) is:
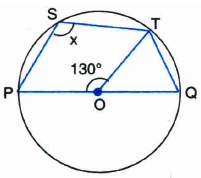 (a)
(a)50°
(b)65°
(c)115°
(d)130°
-
Heron's formula is
(a)\(\Delta =\sqrt { s(s+a)(s+b)(s+c) } \)
(b)\(\Delta =\sqrt { s(s-a)(s-b)(s-c) } \)
(c)\(\Delta =\sqrt { s(s-a)(s-b)(s-c) } \), s=a+b+c
(d)\(\Delta =\sqrt { s(s-a)(s-b)(s-c) } \), 2s=a+b+c
-
A brick measures 25 cm \(\times\) 12 cm \(\times\) 10 cm. Its surface area is
(a)670 cm2
(b)1340 cm2
(c)3000 cm2
(d)1500 cm2
-
In the following frequency distribution, the lower limit of the sixth class is
Marks Numbeo of Students 0-5 3 5-10 5 10-15 8 15-20 12 20-25 7 25-30 3 (a)20
(b)25
(c)30
(d)0.
-
A coin is tossed 200 times.The head appears 79 times.The probability of a tail is:
(a)\(\frac { 79 }{2004 } \)
(b)\(\frac { 121 }{ 200 } \)
(c)1
(d)0
-
If \(a+8\sqrt { 5 } b=\frac { 8+\sqrt { 5 } }{ 8-\sqrt { 5 } } +\frac { 8-\sqrt { 5 } }{ 8+\sqrt { 5 } } \) , find a and b.
(a) -
Find the remainder when the polynomial f(x) = 4x3-12x2+14x-3 is divided by (2x-2).
(a) -
In which quadrant do the given point lie? (-3,5)
(a) -
Find the value of 'm' if x = 2, y = 1 is a solution of the equation 2x + 3y = m and represent it graphically
(a) -
State any two Euclid's axioms.
(a) -
in figure, the sides AB and AC of ABC are produced to pints E and D respectively .If bisectors BO and CO of \(\angle \) CBE and f \(\angle \) BCD respectively meet at point O.then prove that
\(\angle BOC=90^{ 0 }=\frac { 1 }{ 2 } \angle BAC\)
.png)
(b) The sides AB and AC of ABC are produced to pints P and Q respectively If bisectors P and Q respectively If bisectors BO and CO of \(\angle CBP\) and \(\angle \) BCQ respectively meet at point O, prove that
\(\angle BOC=\frac { 1 }{ 2 } (y+z)\)
.png) (a)
(a) -
In given figure AX = BY and \(AX\parallel BY\) .Prove that \(\triangle APX\cong \triangle BPY\)
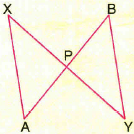 (a)
(a) -
Show that the diagonals of a rhombus are perpendicular to each other.
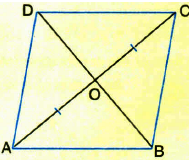 (a)
(a) -
In the figure, the vertex A of \(\Delta \) ABC is joined to a point D on the side BC. The mid-point of AD is E. Prove that ar(\(\Delta \) BEC) =\(\frac { 1 }{ 2 } ar(\Delta ABC)\)
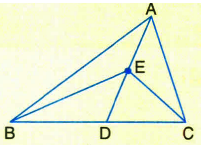 (a)
(a) -
In the given figure, O is the centre of the circle and chord AC and BD intersect at P such that \(\angle\)APB = 120° and \(\angle\)PBC = 15°, find the value of \(\angle\)ADB.
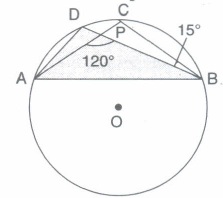 (a)
(a) -
Construct a triangle of sides 3 cm, 3.5 cm and 5 cm. Bisect the smallest angle of the triangle.
(a) -
In the given figure AB CD is a rhombus with AC =16 cm and AB = 10 cm. What is the area of the rhombus ABCD?
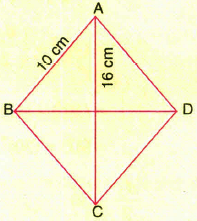 (a)
(a) -
The edge of a cube is 10.5 mm. Find its total surface area in cm2.
(a) -
Calculate mean of prime numbers lying between 6 and 20.
(a) -
A die is tossed 100 times and the data are recorded as below:
Outcomes 1 2 3 4 5 6 Frequency 20 15 20 15 20 10 The die is tossed again. Find the probability of getting:
(i) an odd number
(ii) a prime number(a) -
If \(x=3+2\sqrt { 2 } \) then find the value of \({ \left( x-\frac { 1 }{ x } \right) }^{ 3 }\)
(a) -
If 3a-2b+5c=5 and 6ab+10bc-15ac=14, find the value of \(27a^3+125c^3+90abc-8b^3\)
(a) -
Plot the points (x,y) given in the following table on the plane, choosing suitable units of distance on the axes.
x -2 -1 0 1 3 y 8 7 -1.25 3 -1 (a) -
Express the following linear equation in the form ax+by+c=0 and indicate the values of a, b and c in each case:
x=3y(a) -
Consider two 'postulates' given below:
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid's postulates? Explain.(a) -
In the given figure, if \(\angle BCD=25^0,\angle BAQ=110^o\ and\ \angle ACR=125^o\), then find the values of x, y, z.
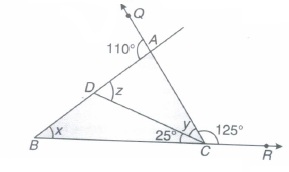 (a)
(a) -
In the given figure, ABC is an isosceles \(\triangle\) in which altitudes BF and CE are drawn to equal sides AC and AB respectively. Show that these altitudes are equal.
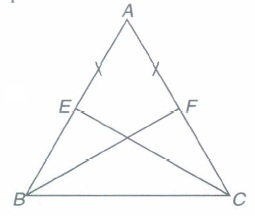 (a)
(a) -
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that\(ar(\Delta APB)\times ar(\Delta CPD)=ar(\Delta APD)\times ar(\Delta BPC)\)
(a) -
If two circles intersect at two points, prove that their centres lie on the perpendicular bisector of the common chord.
(a) -
Construct a triangle ABC in which BC = 8 cm, \(\angle B=45°\) and AB - AC = 2.5 cm.
(a) -
A cylindrical tube opened at both ends is made of iron sheet which is 2 cm thick. If the outer diameter is 16 cm and its length is 100 cm, find how many cubic centimeters of iron has been used in making a tube? (Use \(\pi =\frac { 22 }{ 7 } \))
(a) -
A cricketer has a mean score of 58 runs in nine innings. Find out how many are to be scored in the tenth innings to raise his mean score to 61.
(a) -
Given below is the frequency distribution of salary in Rs of 80 workers in a factory.
Salary No.of workers 1000-2000 8 2000-3000 14 3000-4000 20 4000-5000 24 5000-6000 14 Find the probability that the salary of a worker selected at random is:
(i) Less than 4000
(ii) More than or equal to 3000
(iii) More than or equal to 2000 but less than 5000(a) -
Locate \(\sqrt { 4.5 } \) on the number line.By measurement, BD=2.2 units
(a) -
Prove that \((a+b)^3+(b+c)^3+(c+a)^3-3(a+b)(b+c)(c+a)\) = \(2(a^3+b^3+c^3-3abc)\)
(a) -
The perpendicular distance of a point from the x-axis is 2 units and the perpendicular distance from the y-axis is 3 units.Write the coordinates of the point if it lies in the:
(i) I quadrant
(ii) II quadrant
(iii) III quadrant
(iv) IV quadrant(a) -
Express the following statement as a linear equation in two variables by taking present ages (in years) of father and son as x and y, respectively.Age of father 5 years ago was two years ago was teo years more than 7 times the age of his son at that time.
(a) -
In the given figure AB = BC and BX = BY. Show that AX = CY. State Euclid's Axiom used.
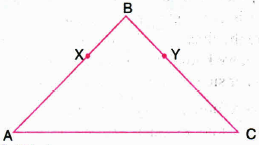 (a)
(a) -
Prove that if one triangle is equal to the sum of the other two angles the triangle is right angled.
(a) -
In given figure, AC == BC, \(\angle\)DCA = \(\angle\)ECB and \(\angle\)DBC = \(\angle\)EAC Prove that \(\angle\)DBC =\(\angle\)EAC and hence DC = EC and BD = AE.
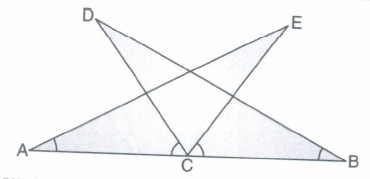 (a)
(a) -
In a quadrilateral ABCD, the line segments bisecting \(\angle \)C and \(\angle \) D meet at E. Prove that \(\angle \)A+\(\angle \)B=2\(\angle \)CED
(a) -
ABCD is a quadrilateral with BD as one of its diagonals and AB = CD=2.5 cm, \(\angle ABD=\angle CDB\) = 90\(°\) and DB = 4 cm. Show that quad. ABCD is a parallelogram and find its area.
(a) -
PQRS is a trapezium with PQ || SR and PS = QR. Prove that the trapezium is cyclic.
(a) -
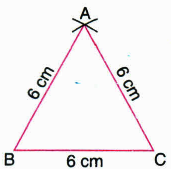
Construct an equilateral triangle with one side 6 cm.
(a) -
A regular hexagon has a side 8 cm. Determine its perimeter and area.
(a) -
A cylinder 3 m high, is open at the top. The circumference of its base is 22 cm. Find its total surface area. \(\left( Take\pi =\frac { 22 }{ 7 } \right) \)
(a) -
Find the mode of the observations 17,23,25,18,17,23,19,23,17,26,23. If 4 is subtracted from each observation, What will be the mode of the new observations?
(a) -
In cricket match, a batsmen hits a boundary 12 times out of 48 balls he plays. Find the probability that he does not hit a boundary in the next ball.
(a) -
Find the value of \(\frac { 4 }{ { \left( 216 \right) }^{ -\frac { 2 }{ 3 } } } +\frac { 1 }{ { \left( 216 \right) }^{ -\frac { 3 }{ 4 } } } +\frac { 2 }{ { \left( 216 \right) }^{ -\frac { 1 }{ 5 } } } \)
(a) -
In the figure below, ABC is a triangle in which AB = AC. X and Yare points on AB and AC such that AX = AY. Prove that \(\triangle ABY\cong \triangle ACX\) .
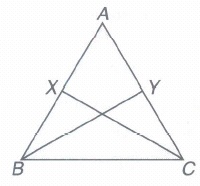 (a)
(a) -
l, m and n are three parallel lines intersected by transversals p and q such that l, m and n cut off equal intercepts AB and BC on p (see Fig.). Show that l, m and n cut off equal intercepts DE and EF on q also.
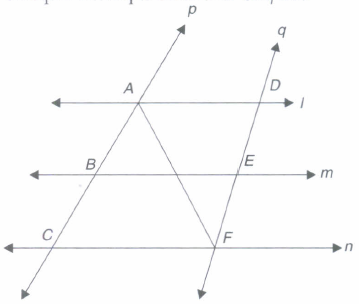 (a)
(a) -
Mr. Mehta, owner of a biscuit manufacturing company, wants to stick butter on a circular biscuit, in the form of two equal chords. He wishes the length of each chord should be more than the radius and less than the diameter of the biscuit. Assuming
that the thickness of the biscuits is negligible.
(i) Prove that the butter-chords subtend equal angles at the centre of the biscuit.
(ii) What is the measure-range of the angle subtended by either butter-chord at the centre?
(iii) Which mathematical concept is used in the above problem?
(iv) Which value is depicted by Mr. Mehta as an owner of a manufacturing company?(a) -
Two solid spheres made of the same metal have masses 5920 g of and 740 g respectively. Determine the radius of the larger sphere, if the diameter of the smaller sphere is 5 cm.
(a) -
Represent the following data by means of a frequency polygon.
Marks Frequency 41-45 4 45-49 10 49-53 15 53-57 18 57-61 20 61-65 12 65-69 13 (a)
Section - A
Section - B
Section - C
Section - D
Section - E
*****************************************
Important Question Part-II Answer Keys
-
(d)
0
-
(a)
p(-1)
-
(c)
3
-
(a)
x+y=48
-
(a)
Thales
-
(c)
\(25^{ 0 }\)
-
(d)
AC > Ab
-
(a)
60°
-
(a)

-
(c)
115°
-
(d)
\(\Delta =\sqrt { s(s-a)(s-b)(s-c) } \), 2s=a+b+c
-
(b)
1340 cm2
-
(b)
25
-
(b)
\(\frac { 121 }{ 200 } \)
-
\(a=\frac { 138 }{ 59 } ,b=0\)
-
2x-1 = 0
\(\Rightarrow \ x=\frac { 1 }{ 2 } \)
By remainder theorem, if f(x) is divided by 2x-1, the remainder is \(f\left( \frac { 1 }{ 2 } \right) \)
\(\therefore \quad f\left( \frac { 1 }{ 2 } \right) =4{ \left( \frac { 1 }{ 2 } \right) }^{ 3 }-12{ \left( \frac { 1 }{ 2 } \right) }^{ 2 }+14\left( \frac { 1 }{ 2 } \right) -3\)
\(=4\times \frac { 1 }{ 8 } -12\times \frac { 1 }{ 4 } +14\times \frac { 1 }{ 2 } -3\)
\(=\frac { 1 }{ 2 } -3+7-3\)
\(=\frac { 1 }{ 2 } +1\)
\(=\frac { 3 }{ 2 } \)
Hence required remainder is \(\frac { 3 }{ 2 } \). -
II
-
m=7
-
Euclid's axioms
(i) Things which are equal to the same thing are equal to one another.
(ii) If equals are added to equals, the wholes are equal. -
-
-
-
-
In \(\Delta\)PCB,
\(\angle\)PCB + \(\angle\)PBC = \(\angle\)APB (exterior angle of a \(\Delta\) is equal to the sum of two opposite angles)
\(\angle\)PCB + 15° = 120°
\(\therefore\) \(\angle\)PCB = 105°
or, \(\angle\)ACB = 105°
\(\Rightarrow\)\(\angle\)ADB = \(\angle\)ACB = 105° [Angle in same sagment] -
-
96 cm2
-
6.615 cm2
-
Prime numbers lying between 6 and 20 are 7,11,13,17,19
Mean = \(\frac{7+11+13+17+19}{5}=\frac{67}{5}\)
= 13.4 -
(i) Total number of cases=100
Number of cases favourable to an odd number (1,3,5) = 20 + 20 + 20 = 60
P(odd number)\(=\frac{60}{100}=\frac{3}{5}\)
(ii) Number of cases favourable to the event a prime number (2,3,5) = 15 + 20 + 20 = 55
P(Prime number) = \(\frac{55}{100}=\frac{11}{20}\) -
\(128\sqrt { 2 } \)
-
20
-
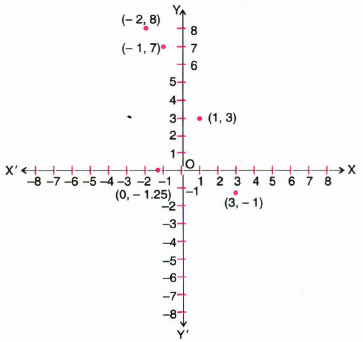
-
x=3y
x-3y+0=0
Comparing with ax+by+c=0, we get
a=1, b=-3, c=0. -
Yes! These postulates contain two undefined terms: Point and Line. Yes! These postulates are consistent because they deal with two different situations
(i) says that given two points A and B, there is a point C lying on the line in between them,
(ii) says that given A and B, we can take C not lying on the line through A and B. These 'postulates' do not follow from Euclid's postulates, however, they follow from Axiom 'Given two distinct lines, there is a unique line that passes through them. -
y=180o-(25o+125o)(Linear pair)
\(\Rightarrow\) y=30o
y+z=110o (Exterior angle)
z=110o-30o=80o
x+25o=z (Exterior angle)
x=80o-25o=55o -
Proof: In \(\triangle\)ABF and \(\triangle\)ACE,
AB =AC
\(\angle\)A =\(\angle\)A
AF = AE
\(\therefore\) \(\triangle\)ABF = \(\triangle\)ACE (by SAS cong.)
\(\therefore\) By c.p.c.t BF = CE.
Alternative Method:
AB = AC\(\Rightarrow \frac { AB }{ 2 } =\frac { AC }{ 2 } \)
\(\Rightarrow \) AE = AF,
sice E and F are the mid-points of AB and AC
In \(\triangle\)ABF and \(\triangle\)ACE,
AB = AC (Given)
\(\angle\)A = \(\angle\)A (Common)
AF = AE (Proved)
\(\therefore \ \triangle ABF\cong \triangle ACE\) (By SAS cong.)
\(\therefore\) BF = CE. (By c.p.c.t) -
Given: Diagonals AC and BD of a quadrilateral ABCD intersect each other at P.
To Prove: \(ar(\Delta APB)\times ar(\Delta CPD)=ar(\Delta APD)\times ar(\Delta BPC)\)
Construction: From A and C, draw perpendiculars AE and CF respectively to BD.
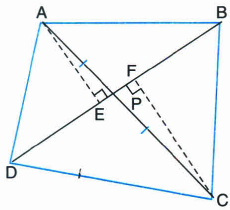
\(ar(\Delta APB)\times ar(\Delta CPD)\)=\(\frac { (PB)(AE) }{ 2 } \times \left( \frac { DP\times CF }{ 2 } \right) \)
|Area of \(\Delta\)=\(\frac { Base\times Corresponding\ altitude }{ 2 } \)
\(=\frac { 1 }{ 4 } (PB)(AE)(DP)(CF)\quad \quad ....(1)\)
\(\\ ar(\Delta APD)\times ar(\Delta BPC)\)
\(\\ =\frac { (DP)(AE) }{ 2 } \times \frac { (PB)(CF) }{ 2 }\)
\( \\ =\frac { 1 }{ 4 } (PB)(AE)(DP)(CF)\quad \quad ....(2)\)
From (1) and (2),
\(ar(\Delta APD)\times ar(\Delta BPC)\) -
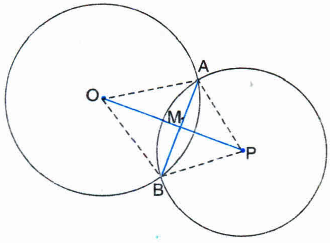
Given: Two circles with centres O and P intersecting at A and B.
Prove: OP is the perpendicular bisector of AB.
Construction: Join OA, OB, PA and PB. Let OP intersect AB at M.
Proof: In \(\Delta \) OAP and \(\Delta \) OBP,
OA = OB | Radii of a circle
PA = PB I Radii of a circle
OP = OP I Common
∴ \(\Delta \ OAP\cong \Delta \ OBP\) I SSS Rule
∴ \(\angle AOP=\angle BOP\) I CPCT
⇒\(\angle AOM=\angle BOM\) ...(1)
In \(\Delta \) AOM and \(\Delta \) BOM,
OA = OB I Radii of a circle
\(\angle AOM=\angle BOM\) | From (1)
OM = OM I Common
∴\(\Delta AOM\cong \Delta BOM\) I SAS Rule
∴ AM = BM ...(2)
I CPCT
and \(\angle AMO=\angle BMO\) ... (3)
I CPCT
But \(\angle AMO+\angle BMO=180°\) I Linear Pair Axiom
∴ \(\angle AMO+\angle BMO=90°\) ...(4)
∴ OM, i.e., OP is the perpendicular bisector of AB. I From (2) and (4) -
-
8800 cm3
-
88
-
\((i)\frac { 21 }{ 40 }\)
\((ii)\frac { 29 }{ 40 }\)
\((iii)\frac { 29 }{ 40 } \) -
Mark the distance 4.5 units from a fixed point A on a given line to obtain a point B such that AB=4.5 units.From B, mark a distance of 1 unit and mark the new point as C.Find the mid-point of AC and mark that point as O.Draw a semi-circle with centre O and radius OC.Draw a semi-circle with Centre O and radius OC.Draw a line perpendicular to AC passing through B and intersecting the semi-circle at D.Then BD=\(\sqrt { 4.5 } \). By measurement,
BD = 2.2 units
\(\sqrt { 4.5 } \)= 2.2
Now, let us treat the line BC as the number line, with B as zero, C as 1 and so on.Draw an arc with centre B and radius BD, which intersects the number line in E. -
L.H.S=\((a+b)^3+(b+c)^3+(c+a)^3-3(a+b)(b+c)(c+a)\)
\(=\left\{ (a+b)+(b+c)+(c+a) \right\} [(a+b)^2+(b+c)^2+(c+a)^2-(a+b)(b+c-(b_c)(c+a)-(c+a)(a+b)]\)
\(=2(a+b+c)[a^2+2ab+b^2+b^2+2bc+c^2+c^2+2ca+c^2-ab-ac-b^2-bc-bc-ba-c^2-ca-ca-cb-a^2-ab]\)
Using Identity I
\(=2(a+b+c)(a^2+b^2+c^2-ab-bc-ca)\)
\(=2(a^3+b^3+c^3-3abc)\)Using Identity VIII -
(i) (3,2)
(ii) (-3,2)
(iii) (-3,-2)
(iv)(3,-2) -
Let the present ages of father and son be x years and y year respectively.
Then, Age of father 5 years ago =(x-5)years
Age of his son 5 years ago(y-5) years
According to the question,
x-5=7(y-5)+2
x-y=7y-35+2
x-7y+28=0
which is the required linear equation in two variables. -
We have
AB = BC
\(\Rightarrow \) AB - BX = BC - BX
|If equals are subtracted from equals, the remainders are equal (Euclid's Axiom (iii))
AB - BX = BC - BY \(|\)\( \because\) BX = BY
AB - BX coincides with AX;
BC - BY coincides with CY
[Things which coincide with one another are equal to one another (Euclid's Axiom (iv))] -
Let in \(\triangle \)ABC \(\angle A=\angle B+\angle C\)
We know that \(\angle A=\angle B+\angle C=180^{ 0 }\)
The sum of the three angles of a triangle is \(180^{ 0 }\)\(\Rightarrow \angle A+\angle A=180^{ 0 }\)
\(\Rightarrow 2\angle A=180^{ 0 }\)
\(\Rightarrow \angle A=\frac { 180^{ 0 } }{ 2 } =90^{ 0 }\)
Hence Traingle ABC is right angled traingle. -
We have, \(\angle\)DCA = \(\angle\)ECB
\(\angle\)DCA + \(\angle\)DCE = \(\angle\)DCE + \(\angle\)ECB
(Adding \(\angle\)DCE on both the sides)
\(\Rightarrow\)\(\angle\)ACE =\(\angle\)BCD ...(i)
Now, in \(\triangle\)s BDC and \(\triangle\)AEC,
\(\angle\)BCD = \(\angle\)ACE [From (i)]
BC = AC (Given)
and \(\angle\)DBC = \(\angle\)EAC (Given)
So, by ASA criterion of congruence, we have
\(\angle\)DBC = \(\angle\)EAC
\(\therefore\) BD = AE and DC == EC
(\(\because\) Corresponding parts of congruent triangles are equal) -
Given: In a quadrilateral ABCD, the line segments bisecting \(\angle \)C and \(\angle \)D meet at E.
To Prove: \(\angle \)A+\(\angle \)B = 2 \(\angle \)CED
I Angle sum property of a quadrilateral
In \(\Delta \) CED,
\(\angle \)CED +\(\angle \)EDC+\(\angle \)ECD = \(180°\) | Angle sum property of a triangle
⇒ \(\angle \) CED+\(1\over2\)\(\angle \)D+ \(1\over2\)\(\angle \)C=\(180°\)
⇒ 2\(\angle \)CED +\(\angle \) D+\(\angle \)C =\(360°\) ...(2)
From (1) .and (2),
2\(\angle \)CED+\(\angle \)D+C=A+B+C+D
⇒ 2 \(\angle \)CED =\(\angle \)A+\(\angle \)B
⇒ \(\angle \)A+\(\angle \)B=2\(\angle \)CED -
DB is the transversal because DC||AB
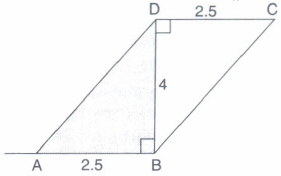
because \(\angle CDB=\angle ABD=90°\)(form a pair of alternate angles)
DC || AB and DC = AB
\(\therefore\) ABCD is a ||gm
ar(ABCD) = b\(\times\)h
= 2.5 \(\times\)4 = 10 cm2. -
Construction: Draw RM II SP meeting PQ M.
Proof: PQ||SR (Given)
PS||MR (Construction)
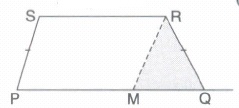
\(\therefore\)PMRS is a parallelogram
\(\therefore\) \(\angle\)S = \(\angle\)PMR
In \(\triangle\)RMQ, RM = RQ (as RM = SP, opp. sides of a parallelogram and PS = QR)
\(\therefore\) \(\angle\)RMQ=\(\angle\)Q
But \(\angle\)RMQ = 180° - \(\angle\)PMR (linear pair)
= 180°- \(\angle\)S. (proved)
\(\therefore\) \(\angle\)Q = 180°- \(\angle\)S
Hence \(\angle\)Q + \(\angle\)S = 180°
Since one pair of opposite angles is supplementary, PQRS is cyclic. Proved. -
Steps of Construction
1. Draw BC = 6 cm.
2. With B as centre and 6 cm as radius, draw an arc on one side of BC.
3. With C as centre and 6 cm as radius, draw another arc on the same side of BC to intersect the former arc at A.
4. Join AB and AC. Then, \(\Delta \) ABC is the required equilateral triangle.
-
\(\therefore \) Side = 8 cm
\(\therefore \) Perimeter = 6\(\times \)8 = 48 cm
Area of equilateral triangle OAB = \(\frac { \sqrt { 3 } }{ 4 } \) (side)2
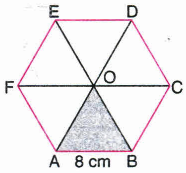
= \(\frac { \sqrt { 3 } }{ 4 } \)(8)2 = 16 \(\sqrt { 3 } \) cm2
\(\therefore \) Area of the regular hexagon = 6 Area of equilateral triangle OAB
= 6\(\times \)16\(\sqrt { 3 } \) = 96\(\sqrt { 3 } \) cm2. -
Let the base radius of the cylinder be r cm. Then,
\(2\pi r=22\)
\(\\ \Rightarrow \ 2\times \frac { 22 }{ 7 } \times r=22\)
\(\\ \Rightarrow r=\frac { 7 }{ 2 } \)
\( h=3m\)
\(\therefore \) Total surface area
\(=2\pi rh+\pi { r }^{ 2 }\)
\(\\ =2\times \frac { 22 }{ 7 } \times \frac { 7 }{ 2 } \times 3+\frac { 22 }{ 7 } \times \frac { 7 }{ 2 } \times \frac { 7 }{ 2 } \)
\(\\ =66+38.5\)
\(\\ =104.5{ m }^{ 2 }\) -
Arranging the data in ascending order, we have,
17,17,17,18,19,23,23,23,23,25,26
Here, 23 occurs most frequency (4 times)
\(\therefore\) Mode = 23
IF = f 4 is subtracted from each observation, then the new observations are
13,13,13,14,15,19,19,19,19,21,22
Here, 19 occurs most frequency (4 times)
\(\therefore\) Mode = 19 -
Let E be the event the batsman hits a boundary.
Then \(\overline E\) is the event the batsman does not hit a boundary.
P(E) = \(\frac{12}{48}=\frac{1}{4}\)
\(\Rightarrow P(\overline E)=1-P(E)\)
\(=1-\frac{1}{4}=\frac{3}{4}\) -
\(\frac { 4 }{ { \left( 216 \right) }^{ -\frac { 2 }{ 3 } } } +\frac { 1 }{ { \left( 216 \right) }^{ -\frac { 3 }{ 4 } } } +\frac { 2 }{ { \left( 216 \right) }^{ -\frac { 1 }{ 5 } } } \)
\(=\frac { 4 }{ { \left( { 6 }^{ 3 } \right) }^{ -\frac { 2 }{ 3 } } } +\frac { 1 }{ { \left( { 4 }^{ 4 } \right) }^{ -\frac { 3 }{ 4 } } } +\frac { 2 }{ { \left( { 3 }^{ 5 } \right) }^{ -\frac { 1 }{ 5 } } } \)
\(=\frac { 4 }{ { 6 }^{ -2 } } +\frac { 1 }{ { 4 }^{ -3 } } +\frac { 2 }{ { 3 }^{ -1 } } \)
\(=\frac { 4 }{ { 36 }^{ -1 } } +\frac { 4 }{ { 64 }^{ -1 } } +\frac { 2 }{ { 3 }^{ -1 } } \)
= 4 x 36 + 1 x 64 + 2 x 3
= 214 -
In \(\triangle\)ABY and \(\triangle\)ACX,
AB = AC (Given)
AY = AX (Given)
\(\angle\)A =\(\angle\)A (Common)
\(\therefore\) By SAS, \(\triangle ABY\cong \triangle ACX\) -
We are given that AB = BC and have to prove that
DE = EF.
Let us join A to E intersecting m at G.
Let trapezium ACFD is divided into two triangles, namely ΔACF and ΔAFD.
In ΔACF, it is given that B is the mid-point of AC(AB = BC) and BG II CF (Since m || n)
So, G is the mid-point of AF (By the converse of midpoint theorem)
Now in ΔAFD, we can apply the sam argument as G is the mid-point of AF, GE IIAD so E is the mid-point of DF
i.e., DE = EF
In otherwords l, m and n cut off equal intercepts on q also. -
(i) Let the butter-chords of the biscuit be AB and CD; and the centre of the biscuit be O.
Join each of A, B, C, D to O.
In \(\triangle\)OAB and In \(\triangle\)OAB and \(\triangle\)OCD,
AB = CD (given)
OA = OC (each equal to radius)
OB =OD
(each equal to radius)
\(\therefore \triangle OAB\cong \triangle OCD\) [S.S.S.]
\(\Rightarrow\) \(\angle\)AOB = \(\angle\)COD (c.p.c.t)
Therefore, the butter-chords subtend equal angles at the centre of the biscuit
\(\Rightarrow\) \(\angle\)AOB = \(\angle\)COD (c.p.c.t)
Therefore, the butter-chords subtend equal angles at the centre of the biscuit.
(ii) We are given the length of either chord is greater than the radius and less than diameter of the circle.
Let length of either chord = l, radius = r, and angle subtended by either butter-chord = 0
Two cases arise:
Case I. If I = r
In this case, the chord and the corresponding radius
form an equilateral triangle with side r
\(\therefore\) \(\theta\)=60°
Case II. If l = 2r
In this case, the butter-chord passes through the centre.
\(\therefore\) \(\theta\) = 180°
Consequently, we arrive at the following inequality :
60° < 8 < 180°
(Asr < 1< 2r)
Thus, the required range is excluding both.
(iii) (a) Congruency of triangles.
(b) c.p.c.t. (Corresponding parts of congruent triangles are equal.)
(c) Equilateral triangle and its angles
(iv) Industrialist, Thoughtfulness, Self-confidence, Rationality. -
Let r and R be the radii of the smaller and larger spheres respectively, we have
\(r=\frac { 5 }{ 2 } cm\)
Volume of the smaller sphere \(=\frac { 4 }{ 3 } \pi { r }^{ 3 }=\frac { 4 }{ 3 } \pi { \left( \frac { 5 }{ 2 } \right) }^{ 3 }\)
\(=\frac { 4 }{ 3 } \times \pi \times \frac { 125 }{ 8 } { cm }^{ 3 }\)
Density of metal\(=\frac { mass }{ Valume } \)
\(=\frac { 740 }{ \frac { 4 }{ 3 } \pi \times \frac { 125 }{ 8 } } g\quad { cm }^{ 3 }\) ...........(i)
Volume of larger sphere = \(\frac { 4 }{ 3 } \pi { R }^{ 3 }\)
Density of metal=\(\frac { mass }{ Volume } =\frac { 5920 }{ \frac { 4 }{ 3 } \pi { R }^{ 3 } } \) ......(ii)
From (i) and (ii), we have
\(\frac { 740 }{ \frac { 4 }{ 3 } \pi \times \frac { 125 }{ 8 } } =\frac { 5920 }{ \frac { 4 }{ 3 } \pi { R }^{ 3 } } \)
\(\Rightarrow \quad { R }^{ 3 }=\frac { 5920\times 125 }{ 740\times 8 } \)
= 125
\(\Rightarrow\) R = 5 cm. -
Marks Frequency Class Marks 37-41 0 39 41-45 4 43 45-49 10 47 49-53 15 51 53-57 18 55 57-61 20 59 61-65 12 53 65-69 13 67 69-73 0 71 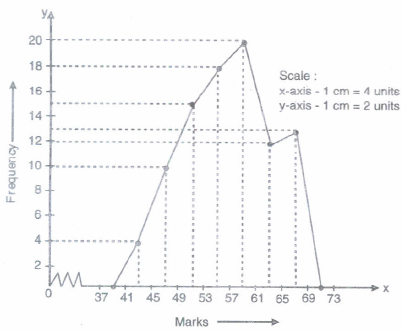
Section - A
Section - B
Section - C
Section - D
Section - E

























