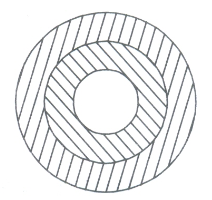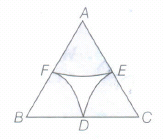Area of the circle=1256cm²
⇒ A=πr²
A.T.Q 1256=πr²
\({1256\over3.14}=r^2\)
\(⇒\sqrt{1256\over 3.14}=r\)
​​​​​
⇒ 20cm = radius
⇒ 40cm = diameter
Here, Diagonals of rhombus = diameter of the circle
∴ Area of rhombus = \({1\over 2}d_1\times d_2\)
\(={1\over 2}\times40\times40=800cm^2\) 

Area of wheel=1.54m²
A=πr²
1.54=πr²
\(⇒\ {1.54\over \pi}=r^2\)
\(⇒\ {154\times7\over 22\times100}=r^2\)
\(⇒\ {49\over 100}=r^2\)
\(⇒{7\over 10}=r\)
⇒Radius of wheel=\({7\over 10}m\)
∴ Circumference of wheel=2πr
\(=2\times{22\over 7}\times{7\over10}={44\over 10}=4.4m\)
Distance covered in one revolution=4.4m
No. of revolution=\({total\ diatance\over distance\ covered\ in\ one\ revolution}\)
\(={176\over 4.4}=40\)

Let,diameter of inner most circle = x
Diameter of middle circle = 2x
Diameter of outer most circle = 3x
∴ Area of inner most circle = π(x)²
Area of middle circle =π(4x² - x²)
=π(3x²)
Area of outer most circle =π(3x)²-π(2x)²
=π(9x² - 4x²)
=π X 5x²
Ratio of the areas of three regions.
πx²: π(3x²):π(5x²)=1:3:5

33 cm

Given, triangle ABC is an equilateral triangle.
\(\therefore \quad \angle A=\angle B=\angle C={ 60 }^{ 0 }\quad and\quad radius,\quad r=\frac { 10 }{ 2 } cm=5cm\)
Area of sector AFEA\(=\frac { \theta }{ { 360 }^{ 0 } } \times \pi { r }^{ 2 }\)
\(=\frac { { 60 }^{ 0 } }{ { 360 }^{ 0 } } \times \pi { \times (5) }^{ 2 }\)
\(=\frac { 25 }{ 6 } \pi \quad { cm }^{ 2 }\)
Since, area of all three sectors are equal.
Total area of shaded region
=3 x Area of sector AFEA\(=3\left( \frac { 25 }{ 6 } \pi \right) \)
\(=3\times \frac { 25 }{ 6 } \times 3.14=39.25\quad { cm }^{ 2 }\)
Hence, the area of shaded region is 39.25 cm²