CBSE 10th Standard Maths Subject Areas Related to Circles Ncert Exemplar 4 Marks Questions 2021
By QB365 on 26 May, 2021
QB365 Provides the updated NCERT Examplar Questions for Class 10 Maths, and also provide the detail solution for each and every ncert examplar questions , QB365 will give all kind of study materials will help to get more marks
QB365 - Question Bank Software
CBSE 10th Standard Maths Subject Areas Related to Circles Ncert Exemplar 4 Marks Questions 2021
10th Standard CBSE
-
Reg.No. :
Maths
-
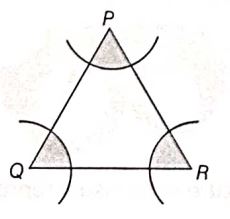
In the given figure, arcs have been drawn with radius 14 cm each and with centres P, Q and R. Find the area of the shaded region.
 (a)
(a) -
In the given figure, arcs have been drawn of radius 21 cm each with vertices A, B, C and D of quadrilateral ABCD as centres. Find the area of the shaded region.
(a) -
Four circular cardboard pieces of radius 7 cm are placed on a paper in such a way that each piece touches other two pieces, Find the area of the portion enclosed between these pieces.
(a) -
In the figure given alongside, a circle is inscribed in a square of side 4 ern and another circle is circumscribing the square. Prove that the area of the circumscribed circle is two times the area of the inscribed circle.
(a) -
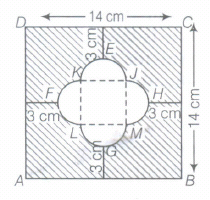
Find the area of the shaded region given in figure.
 (a)
(a)
4 Marks
*****************************************
CBSE 10th Standard Maths Subject Areas Related to Circles Ncert Exemplar 4 Marks Questions 2021 Answer Keys
-
Area of sector with central \(\angle\)P
\(=\frac{\angle P}{360^{\circ}} \times \pi \times(14)^2\)
Area of sector with central \(\angle\)Q
\(=\frac{\angle Q}{360^{\circ}} \times \pi \times(14)^2\)
and area of sector with central \(\angle\)R
\(=\frac{\angle R}{360^{\circ}} \times \pi \times(14)^2\)
Now, area of shaded region
\(=(14)^2 \times \pi \frac{(\angle P+\angle Q+\angle R)}{360^{\circ}}\)
\(=196 \times \pi \times \frac{180^{\circ}}{360^{\circ}}\) [by angle sum property of triangle]
308 cm2 -
1386 cm2
-
42 cm2
-
Let r1=radius of the inscribed circle=\(\frac {4}{2}\)=2 cm
and r2=radius of the circumscribed circle
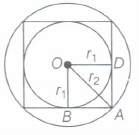
Now, in triangle OBA,
(OA)2=(OB)2+(BA)2
[by Pythagoras theorem].
\(\Rightarrow \quad { r }^{ 2 }={ r }_{ 1 }^{ 2 }+{ r }_{ 1 }^{ 2 }\)
\(\Rightarrow { r }_{ 2 }=\sqrt { 2{ r }_{ 1 }^{ 2 } } \)
\(\Rightarrow { r }_{ 2 }=\sqrt { 2\times { 2 }^{ 2 } } =2\sqrt { 2 } cm\)
Now, area of inscribed circle
\(=\pi { r }_{ 1 }^{ 2 }=\pi { (2) }^{ 2 }=4\pi \quad { cm }^{ 2 }\) ..(i)
and area of circumscribed circle=\(\pi { r }_{ 2 }^{ 2 }=\pi { (2\sqrt { 2 } ) }^{ 2 }=8\pi \quad { cm }^{ 2 }\)
Area of circumscribed circle=\(2(4\pi )\)
=2 x (Area of inscribed circle) [from Eq. (i)] -
There are four equally semi-circles and JKLM formed a square
\(\therefore\) FH=14-(3+3)=8 cm
Let the side of square JKLM be x can
Then, FH=\(\frac { x }{ 2 } +x+\frac { x }{ 2 } \)
\(\Rightarrow\) 8=2x \(\Rightarrow\) x=4
So, the side of square should be 4 cm and radius of semi-circle of both ends are 2 cm each.
\(\therefore\) Area of square JKLm=(4)2=16 cm2
Area of semi-circle JHM=\(\frac { \pi { r }^{ 2 } }{ 2 } \)
\(=\frac { \pi \times (2)^{ 2 } }{ 2 } =2\pi \quad { cm }^{ 2 }\)
\(\therefore\) Area of four semi-circles=\(4\times 2\pi \)
Now, area of square ABCD=(14)2=196 cm2
\(\therefore\) Area of shaded region=Area of square ABCD-(Area of four semi-circles + Area of square JKLM)
\(=196-(8\pi +16)=196-16-8\pi \)
\(=(180-8\pi ){ cm }^{ 2 }\)
Hence, the required of the shaded region is \((180-8\pi ){ cm }^{ 2 }\)
4 Marks

























