CBSE 10th Standard Maths Subject Case Study Questions 2021
By QB365 on 21 May, 2021
QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 10th Standard Maths Subject Case Study Questions 2021
10th Standard CBSE
-
Reg.No. :
Maths
-
Transport department of a city wants to buy some Electric buses for the city. For which they wants to analyse the distance travelled by existing public transport buses in a day.

The following data shows the distance travelled by 60 existing public transport buses in a day.Daily distance travelled (in km) 200-209 210-219 220-229 230-239 240-249 Number of buses 4 14 26 10 6 Based on the above information, answer the following questions.
(i) The upper limit of a class and lower limit of its succeeding class is differ by(a) 9 (b) 1 (c) 10 (d) none of these (ii) The median class is
(a) 229.5-239.5 (b) 230-239 (c) 220-229 (d) 219.5-229.5 (iii) The cumulative frequency of the class preceding the median class is
(a) 14 (b) 18 (c) 26 (d) 10 (iv) The median of the distance travelled is
(a) 222 km (b) 225 km (c) 223 km (d) none of these (v) If the mode of the distance travelled is 223.78 km, then mean of the distance travelled by the bus is
(a) 225 km (b) 220 km (c) 230.29 km (d) 224.29 km (a) -
An electric scooter manufacturing company wants to declare the mileage of their electric scooters. For this, they recorded the mileage (km/ charge) of 50 scooters of the same model. Details of which are given in the following table.
Mileage (km/charge) 100-120 120-140 140-160 160-180 Number of scooters 7 12 18 13 
Based on the above information, answer the following questions.
(i) The average mileage is(a) 140 krn/charge (b) 150 krn/ charge (c) 130 krn/charge (d) 144.8 krn/charge (ii) The modal value of the given data is
(a) 150 (b) 150.91 (c) 145.6 (d) 140.9 (ill) The median value of the given data is
(a) 140 (b) 146.67 (c) 130 (d) 136.6 (iv) Assumed mean method is useful in determining the
(a) Mean (b) Median (c) Mode (d) All of these (v) The manufacturer can claim that the mileage for his scooter is
(a) 144 krn/charge (b) 155 krn/charge (c) 165 krn/charge (d) 175krn/charge (a) -
Household income in India was drastically impacted due to the COVID-19 loekdown. Most of the companies decided to bring down the salaries of the employees by 50%.
The following table shows the salaries (in percent) received by 25 employees during loekdown.Salaries received (in percent) 50-60 60-70 70-80 80-90 Number of employees 9 6 8 2 
Based on the above information, answer the following questions.
(i) Total number of persons whose salary is reduced by more than 30%, is(a) 10 (b) 20 (c) 25 (d) 15 (ii) Total number of persons whose salary is reduced by atmost 40%, is
(a) 15 (b) 10 (c) 16 (d) 8 (iii) The modal class is
(a) 50-60 (b) 60-70 (c) 70-80 (d) 80-90 (iv) The median class of the given data is
(a) 50-60 (b) 60-70 (c) 70-80 (d) 80-90 (v) The empirical relationship between mean, median and mode is
(a) 3 Median = Mode + 2 Mean (b) 3 Median = Mode - 2 Mean (c) Median = 3 Mode - 2 Mean (d) Median = 3 Mode + 2 Mean (a) -
A petrol pump owner wants to analyse the daily need of diesel at the pump. For this he collected the data of vehicles visited in 1 hr. The following frequency distribution table shows the classification of the number of vehicles and quantity of diesel filled in them.
Diesel Filled (in Litres) 3-5 5-7 7-9 9-11 11-13 Number of vehicles 5 10 10 7 8 
Based on the above data, answer the following questions.
(i) Which of the following is correct?(a) If xi and fi are sufficiently small, then direct method is appropriate choice for calculating mean. (b) If xi and fi are sufficiently large, then direct method is appropriate choice for calculating mean. (c) If xi and fi are sufficiently small, then assumed mean method is appropriate choice for calculating mean. (d) None of the above. (ii) Average diesel required for a vehicle is
(a) 8.15 litres (b) 6 litres (c) 7 litres (d) 5.5 litres (iii) If approximately 2000 vehicles comes daily at the petrol pump, then how much litres of diesel the pump should have?
(a) 16200 litres (b) 16300 litres (c) 10600 litres (d) 15000 litres (iv) The sum of upper and lower limit of median class is
(a) 22 (b) 10 (c) 16 (d) none of these (v) If the median of given data is 8litres, then mode will be equal to
(a) 7.5 litres (b) 7.7 litres (c) 5.7 litres (d) 8 litres (a) -
Two friends Richa and Sohan have some savings in their piggy bank. They decided to count the total coins they both had. After counting they find that they have fifty \(\begin{equation} ₹ \end{equation} \) 1 coins, forty eight \(\begin{equation} ₹ \end{equation} \) 2 coins, thirty six \(\begin{equation} ₹ \end{equation} \) 5 coins, twenty eight \(\begin{equation} ₹ \end{equation} \)10 coins and eight \(\begin{equation} ₹ \end{equation} \) 20 coins. Now, they said to Nisha, their another friends, to choose a coin randomly.
Find the probability that the coin chosen is

(i) \(\begin{equation} ₹ \end{equation} \)5 coin(a) \(\begin{equation} \frac{17}{55} \end{equation}\) (b) \(\begin{equation} \frac{36}{85} \end{equation}\) (c) \(\begin{equation} \frac{18}{85} \end{equation}\) (d) \(\begin{equation} \frac{1}{15} \end{equation}\) (ii) \(\begin{equation} ₹ \end{equation} \) 20 coin
(a) \(\begin{equation} \frac{13}{85} \end{equation}\) (b) \(\begin{equation} \frac{4}{85} \end{equation}\) (c) \(\begin{equation} \frac{3}{85} \end{equation}\) (d) \(\begin{equation} \frac{4}{15} \end{equation}\) (iii) not a \(\begin{equation} ₹ \end{equation} \) 10 coin
(a) \(\begin{equation} \frac{15}{31} \end{equation}\) (b) \(\begin{equation} \frac{36}{85} \end{equation}\) (c) \(\begin{equation} \frac{1}{5} \end{equation}\) (d) \(\begin{equation} \frac{71}{85} \end{equation}\) (iv) of denomination of atleast \(\begin{equation} ₹ \end{equation} \)10.
(a) \(\begin{equation} \frac{18}{85} \end{equation}\) (b) \(\begin{equation} \frac{36}{85} \end{equation}\) (c) \(\begin{equation} \frac{1}{17} \end{equation}\) (d) \(\begin{equation} \frac{16}{85} \end{equation}\) (v) of denomination of atmost \(\begin{equation} ₹ \end{equation} \) 5.
(a) \(\begin{equation} \frac{67}{85} \end{equation}\) (b) \(\begin{equation} \frac{36}{85} \end{equation}\) (c) \(\begin{equation} \frac{4}{85} \end{equation}\) (d) \(\begin{equation} \frac{18}{85} \end{equation}\) (a) -
Rohit wants to distribute chocolates in his class on his birthday. The chocolates are of three types: Milk chocolate, White chocolate and Dark chocolate. If the total number of students in the class is 54 and everyone gets a chocolate, then answer the following questions.

(i) If the probability of distributing milk chocolates is 1/3, then the number of milk chocolates Rohit has, is(a) 18 (b) 20 (c) 22 (d) 30 (ii) If the probability of distributing dark chocolates is 4/9, then the number of dark chocolates Rohit has, is
(a) 18 (b) 25 (c) 24 (d) 36 (iii) The probability of distributing white chocolates is
(a) \(\begin{equation} \frac{11}{27} \end{equation}\) (b)\(\begin{equation} \frac{8}{21} \end{equation}\) (c) \(\begin{equation} \frac{1}{9} \end{equation}\) (d) \(\begin{equation} \frac{2}{9} \end{equation}\)
(iv) The probability of distributing both milk and white chocolates is(a) \(\begin{equation} \frac{3}{17} \end{equation}\) (b) \(\begin{equation} \frac{5}{9} \end{equation}\) (c) \(\begin{equation} \frac{1}{3} \end{equation}\) (d) \(\begin{equation} \frac{1}{27} \end{equation}\) (v) The probability of distributing all the chocolates is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{3}{4} \end{equation}\) (a) -
Prateek goes to a toy shop to purchase a building block kit for his son. He found that the kit contains 120 blocks, of which 40 are red, 25 are blue, 30 are green and the rest are yellow. His son picks up a block at random. Find the probability that the block is

(i) of red colour(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{1}{3} \end{equation}\) (ii) not of yellow colour
(a) \(\begin{equation} \frac{1}{6} \end{equation}\) (b) \(\begin{equation} \frac{1}{4} \end{equation}\) (c) \(\begin{equation} \frac{19}{24} \end{equation}\) (d) \(\begin{equation} \frac{19}{25} \end{equation}\) (iii) of green colour
(a) \(\begin{equation} \frac{1}{8} \end{equation}\) (b) \(\begin{equation} \frac{1}{10} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{12} \end{equation}\) (iv) of yellow colour
(a) \(\begin{equation} \frac{15}{118} \end{equation}\) (b) \(\begin{equation} \frac{5}{24} \end{equation}\) (c) \(\begin{equation} \frac{17}{24} \end{equation}\) (d) \(\begin{equation} \frac{19}{50} \end{equation}\) (v) not of blue colour
(a) \(\begin{equation} \frac{1}{8} \end{equation}\) (b) \(\begin{equation} \frac{19}{24} \end{equation}\) (c) \(\begin{equation} \frac{19}{31} \end{equation}\) (d) \(\begin{equation} \frac{16}{55} \end{equation}\) (a) -
Sunil goes to market for buying an aquarium for his house. He asked to the shopkeeper to put some fish in the aquarium. The shopkeeper takes out 13 guppy fish, 18 flowerhorn fish, 12 koi fish and 11 angel fish from the big tank he had and put them in the aquarium that Sunil had bought. Now, he selects a fish at random.

On the basis of above information, answer the following questions.
(i) If total number of male fish in the aquarium is 36, then the probability of selecting a female fish is(a) \(\begin{equation} \frac{1}{2} \end{equation}\) (b) \(\begin{equation} \frac{1}{3} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{5} \end{equation}\) (ii) The probability of selecting a flowerhorn fish is
(a) \(\begin{equation} \frac{1}{2} \end{equation}\) (b) \(\begin{equation} \frac{1}{3} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{5} \end{equation}\) (iii) The probability of not selecting a koi fish is
(a) \(\begin{equation} \frac{2}{9} \end{equation}\) (b) \(\begin{equation} \frac{1}{3} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{7}{9} \end{equation}\) (iv) The probability of selecting neither angle fish nor flowerhorn fish is
(a) \(\begin{equation} \frac{16}{27} \end{equation}\) (b) \(\begin{equation} \frac{25}{54} \end{equation}\) (c) \(\begin{equation} \frac{8}{27} \end{equation}\) (d) \(\begin{equation} \frac{25}{27} \end{equation}\) (v) The probability of selecting a guppy fish is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{13}{54} \end{equation}\) (d) None of these (a) -
Two friends were playing a game with two dice. Anju has a blue dice and Nitish has a grey dice. They decided to throw both the dice simultaneously and note down all the possible outcomes appearing on the top of both the dice.

On the basis of above information, answer the following questions.
(i) The total number of possible outcomes they noted, is(a) 24 (b) 36 (c) 18 (d) 6 (ii) The probability of getting the sum of numbers on two dice is 16, is
(a) 1 (b) \(\begin{equation} \frac{5}{36} \end{equation}\) (c) 0 (d) \(\begin{equation} \frac{18}{35} \end{equation}\) (iii) The probability that both the numbers are prime numbers, is
(a) 0 (b) \(\begin{equation} \frac{1}{2} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (iv) The probability that product of two numbers is odd, is|
(a) 1 (b) \(\begin{equation} \frac{1}{2} \end{equation}\) (c) \(\begin{equation} \frac{1}{4} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (v) The probability that difference between numbers is zero, is
(a) \(\begin{equation} \frac{1}{2} \end{equation}\) (b) \(\begin{equation} \frac{1}{4} \end{equation}\) (c) \(\begin{equation} \frac{1}{6} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (a) -
Four friends are playing with cards. One of them hides all the 2's, 5's and Jacks from the deck of 52 cards and then shuffles the remaining cards. Now, he tells to one of his friend to pick a card at random from the remaining cards.

On the basis of above information, answer the following questions.
(i) The probability of getting '6 of spade' is(a) 0 (b) \(\begin{equation} \frac{1}{20} \end{equation}\) (c) \(\begin{equation} \frac{1}{40} \end{equation}\) (d) 1 (ii) The probability of getting a black diamond is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{1}{4} \end{equation}\) (iii) The probability of getting a face card is
(a) \(\begin{equation} \frac{1}{3} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{1}{7} \end{equation}\) (d) \(\begin{equation} \frac{1}{9} \end{equation}\) (iv) The probability of getting a club is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{1}{4} \end{equation}\) (v) The probability of getting a red card is
(a) 0 (b) 1 (c) \(\begin{equation} \frac{1}{2} \end{equation}\) (d) \(\begin{equation} \frac{1}{4} \end{equation}\)
(a) -
In a toy shop, there is a spinning wheel for their customers. The spinning wheel has different types of prizes as shown in figure. A customer can only spin the wheel after buying something from the shop.
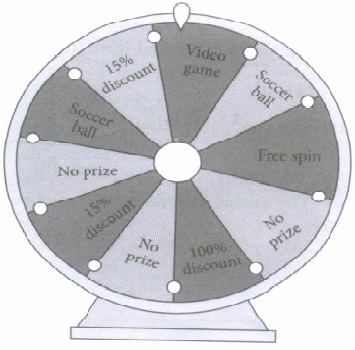
On the basis of above information, answer the following questions.
(i) If Mr Sharma spins the wheel, then the probability that he gets 100% discount is(a) 0 (b) \(\begin{equation} \frac{1}{10} \end{equation}\) (c) \(\begin{equation} \frac{1}{5} \end{equation}\) (d) \(\begin{equation} \frac{1}{4} \end{equation}\) (ii) If Anita spins the wheel, then the probability of getting no prize is
(a) \(\begin{equation} \frac{1}{10} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{3}{10} \end{equation}\) (d) \(\begin{equation} \frac{2}{5} \end{equation}\)
(iii) Anshu spins the wheel, the probability that the wheel stops at soccer ball is(a) \(\begin{equation} \frac{1}{10} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{3}{10} \end{equation}\) (d) \(\begin{equation} \frac{2}{5} \end{equation}\) (iv) The probability that one customer wins 15% discount is
(a) \(\begin{equation} \frac{1}{10} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{3}{10} \end{equation}\) (d) \(\begin{equation} \frac{2}{5} \end{equation}\) (v) The probability of getting a free spin is
(a) \(\begin{equation} \frac{1}{10} \end{equation}\) (b) \(\begin{equation} \frac{1}{5} \end{equation}\) (c) \(\begin{equation} \frac{3}{10} \end{equation}\) (d) \(\begin{equation} \frac{2}{5} \end{equation}\) (a) -
Mr Verma is a production manager in a factory that makes footballs. On one day, he noticed that at every 100
pieces produced in the factory, 15 are defective. If the total number of footballs produced in one day in the
factory is 22000, then answer the following questions.

(i) A football is selected at random, then the probability of selecting a defective football is(a) \(\begin{equation} \frac{1}{20} \end{equation}\) (b) \(\begin{equation} \frac{1}{10} \end{equation}\) (c) \(\begin{equation} \frac{3}{20} \end{equation}\) (d) \(\begin{equation} \frac{1}{5} \end{equation}\) (ii) A football is selected at random, the probability of selecting a non-defective football is
(a) \(\begin{equation} \frac{1}{20} \end{equation}\) (b) \(\begin{equation} \frac{13}{20} \end{equation}\) (c) \(\begin{equation} \frac{3}{4} \end{equation}\) (d) \(\begin{equation} \frac{17}{20} \end{equation}\) (iii) The total number of defective footballs produced in one day is
(a) 4200 (b) 3300 (c) 9200 (d) 11000 (iv) The total number of non-defective footballs produced in one day is
(a) 18700 (b) 17800 (c) 12800 (d) 11000 (v) If the probability of selecting a defective football is , then the number of non-defective footballs produced in one day, if everyday same number of footballs produced in the factory, is
(a) 13640 (b) 9200 (c) 7040 (d) 14960 (a) -
Two families- Gupta's and Singhal's are lived in a colony. Gupta family has two children while Singhal family has 3 children.

On the basis of the above information, answer the following questions.
(i) Find the probability that Mr Singhal has exactly 2 girls and 1 boy.(a) \(\begin{equation} \frac{1}{2} \end{equation}\) (b) \(\begin{equation} \frac{1}{4} \end{equation}\) (c) \(\begin{equation} \frac{1}{6} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (ii) The probability that Gupta's has atleast 1 boy is
(a) \(\begin{equation} \frac{1}{3} \end{equation}\) (b) \(\begin{equation} \frac{2}{3} \end{equation}\) (c) 1 (d) \(\begin{equation} \frac{4}{5} \end{equation}\) (iii) The probability that Gupta's has atmost 1 girl is
(a) \(\begin{equation} \frac{1}{3} \end{equation}\) (b) \(\begin{equation} \frac{2}{3} \end{equation}\) (c) 1 (d) \(\begin{equation} \frac{2}{5} \end{equation}\) (iv) The probability that Singhal's has no boy is
(a) \(\begin{equation} \frac{1}{2} \end{equation}\) (b) \(\begin{equation} \frac{1}{4} \end{equation}\) (c)\(\begin{equation} \frac{1}{6} \end{equation}\) (d) \(\begin{equation} \frac{1}{8} \end{equation}\) (v) The sum of probabilities that both families have exactly two girls is
(a) \(\begin{equation} \frac{1}{12} \end{equation}\) (b) \(\begin{equation} \frac{1}{4} \end{equation}\) (c) \(\begin{equation} \frac{7}{12} \end{equation}\) (d) 0 (a) -
Vishal goes to a store to purchase juice cartons for his shop. The store has 80 cartons of orange juice, 90 cartons of apple juice, 38 cartons of mango juice and 42 cartons of guava juice. If Vishal chooses a carton at random, then answer the following questions.

(i) The probability that the selected carton is of apple juice is(a) \(\begin{equation} \frac{.1}{25} \end{equation}\) (b) \(\begin{equation} \frac{8}{25} \end{equation}\) (c) \(\begin{equation} \frac{13}{25} \end{equation}\) (d) \(\begin{equation} \frac{9}{25} \end{equation}\) (ii) The probability that the selected carton is not of orange juice is
(a) \(\begin{equation} \frac{14}{25} \end{equation}\) (b) \(\begin{equation} \frac{11}{25} \end{equation}\) (c) \(\begin{equation} \frac{17}{25} \end{equation}\) (d) \(\begin{equation} \frac{4}{25} \end{equation}\) (iii) The probability of selecting a carton of guava juice is
(a) \(\begin{equation} \frac{51}{125} \end{equation}\) (b) \(\begin{equation} \frac{16}{125} \end{equation}\) (c) 0 (d) \(\begin{equation} \frac{21}{125} \end{equation}\) (iv) Vishal buys 4 cartons of apple juice, 3 cartons of orange juice and 3 cartons of guava juice. A customer comes to Vishal's shop and picks a tetrapack of juice at random. The probability that the customer picks a guava juice, if each carton has 10 tetrapacks of juice, is
(a) \(\begin{equation} \frac{1}{10} \end{equation}\) (b) \(\begin{equation} \frac{2}{10} \end{equation}\) (c) \(\begin{equation} \frac{3}{10} \end{equation}\) (d) \(\begin{equation} \frac{2}{5} \end{equation}\) (v) If the storekeeper bought 14 more cartons of apple juice, then the probability of selecting a tetrapack of apple juice from the store is
(a) \(\begin{equation} \frac{25}{127} \end{equation}\) (b) \(\begin{equation} \frac{50}{127} \end{equation}\) (c) \(\begin{equation} \frac{75}{127} \end{equation}\) (d) \(\begin{equation} \frac{100}{127} \end{equation}\) (a) -
In the month of May, the weather forecast department gives the prediction of weather for the month of June, The given table shows the probabilities of forecast of different days:
Days Sunny Cloudy Partially cloudy Rainy Probability \(\begin{equation} \frac{1}{2} \end{equation}\) x \(\begin{equation} \frac{1}{5} \end{equation}\) y 
If the forecast is 100% correct for June, then answer the following questions,
(i) The number of sunny days in June, is(a) 5 (b) 10 (c) 15 (d) 20 (ii) If the number of cloudy days in June is 5, then x =
(a) \(\begin{equation} \frac{1}{4} \end{equation}\) (b) \(\begin{equation} \frac{1}{6} \end{equation}\) (c) \(\begin{equation} \frac{1}{8} \end{equation}\) (d) \(\begin{equation} \frac{1}{10} \end{equation}\) (iii) The probability that the day is not rainy is
(a) \(\begin{equation} \frac{13}{15} \end{equation}\) (b) \(\begin{equation} \frac{11}{15} \end{equation}\) (c) \(\begin{equation} \frac{1}{15} \end{equation}\) (d) None of these (iv) If the sum of x < and y is \(\begin{equation} \frac{3}{10} \end{equation}\), then the number of rainy days in June is
(a) 1 (b) 2 (c) 3 (d) 4 (v) Find the number of partially cloudy days
(a) 2 (b) 4 (c) 6 (d) 8 (a)
Case Study Questions
*****************************************
CBSE 10th Standard Maths Subject Case Study Questions 2021 Answer Keys
-
(i) (b): The upper limit of a class and the lower class of its succeeding class differ by 1.
(ii) (d) : Here, class intervals are in inclusive form. So, we first convert them in exclusive form. The frequency distribution table in exclusive form is as follows:Class interval Frequency (fi) Cumulative frequency (c.f) 199.5-209.5 4 4 209.5-219.5 14 18 219.5-229.5 26 44 229.5-239.5 10 54 239.5-249.5 6 60
\(\text { Here, } \Sigma f_{i} \text { i.e., } N=60 \)
\(\Rightarrow \frac{N}{2}=30\)Now, the class interval whose cumulative frequency is
just greater than 30 is 219.5 - 229.5.
\(\therefore\) Median class is 219.5 - 229.5.
(iii) (b): Clearly, the cumulative frequency of the class preceding the median class is 18
(iv) (d): Median \(=l+\left[\frac{\frac{N}{2}-c . f .}{f}\right] \times h\)
\(=219.5+\left(\frac{30-18}{26}\right) \times 10 \)
\(=219.5+\frac{12 \times 10}{26}=219.5+4.62=224.12\)
\(\therefore\) Median of the distance travelled is 224.12 km
(v) (d): We know, Mode = 3 Median - 2 Mean
\(\therefore \quad \text { Mean }=\frac{1}{2}(3 \text { Median }-\text { Mode }) \)
\(=\frac{1}{2}(672.36-223.78)=224.29 \mathrm{~km}\) -
Given frequency distribution table can be drawn as:
Class interval Class mark Frequency (fi) xi fi c.f 100-120 110 7 770 7 120-140 130 12 1560 19 140-160 150 18 2700 37 160-180 170 13 2210 50 Total 50 7240 (i) (d): Clearly, average mileage
\(=\frac{7240}{50}=144.8 \mathrm{~km} / \text { charge }\)
(ii) (b) : Since, highest frequency is IS, therefore,
modal class is 140-160.
Here, l = 140,f1 = 18,f0 = 12,f2 = 13, h = 20
\(\therefore \quad \text { Mode }=140+\frac{18-12}{36-12-13} \times 20=140+\frac{6}{11} \times 20 \)
\(=140+\frac{120}{11}=140+10.91=150.91\)
(iii) (b) : Here \(\frac{N}{2}=\frac{50}{2}=25\) and the corresponding class whose cumulative frequency is just greater than
25 is 140-160.
Here, l = 140, c.f = 19, h = 20 and f= 18
\(\therefore \quad \text { Median }=l+\left(\frac{\frac{N}{2}-c . f .}{f}\right) \times h\)
\(=140+\frac{25-19}{18} \times 20=140+\frac{60}{9}=146.67\)
(iv) (a) : Assumed mean method is useful in determining the mean.
(v) (a): Since, Mean = 144.S, Mode = 150.91 and Median = 146.67 and minimum of which is 144 approx, therefore manufacturer can claim the mileage for his scooter 144 km/charge. -
(i) (d): Required number of persons = 9 + 6 = 15
(ii) (c): Required number of persons = 6 + 8 + 2 = 16
(iii) (a) : 50-60 is the modal class as the maximum frequency is 9.
(iv) (b) : The cumulative frequency distribution table for the given data can be drawn as :Salaries received (in percent) Number of employees (fi) Cumulative frequency c.f 50-60 9 9 60-70 6 9 + 6 = 15 70-80 8 15 + 8 = 23 80-90 2 23 + 2 = 25 Total \(\sum f_{i}=25\) \(\text { Here, } \frac{N}{2}=\frac{25}{2}=12.5\)
The cumulative frequency just greater than 12.5 lies in the interval 60-70.
Hence, the median class is 60-70.
(v) (a): We know, Mode = 3 Median - 2 Mean
\(\therefore\) 3 Median = Mode + 2 Mean. -
(i) (a): If fi and xi are very small, then direct method is appropriate method for calculating mean.
(ii) (a) : The frequency distribution table from the given data can be drawn as :Class Class mark (xi) Frequency fi fi xi 3-5 4 5 20 5-7 6 10 60 7-9 8 10 80 9-11 10 7 70 11-13 12 8 96 Total 40 326 \(\therefore \quad \text { Mean }=\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}=\frac{326}{40}=8.15 \text { litres }\)
(iii) (b) : If 2000 vehicles comes daily and average quantity of diesel required for a vehicle is 8.15 litres, then total quantity of diesel required = 2000 x 8.15
= 16300 litres
(iv) (c) : Here \(N=40 \text { and } \frac{N}{2}=20\) c.f for the distribution are 5, 15,25,32,40
Now, c.f just greater than 20 is 25 which is corresponding to the class interval 7-9.
So median class is 7-9.
\(\therefore\) Required sum of upper limit and lower limit
= 7 + 9 = 16
(v) (b): We know, Mode = 3 Median -2 Mean
= 3(8) - 2(8.15) = 24 - 16.3 = 7.7 -
Total number of coins = 50 + 48 + 36 + 28 + 8 = 170
(i) (c): Number of \(\begin{equation} ₹ \end{equation} \) 5 coins = 36
Required probability = \(\begin{equation} \frac{36}{70}=\frac{18}{85} \end{equation}\)
(ii) (b): Number of \(\begin{equation} ₹ \end{equation} \)20 coins = 8
Required probability = \(\begin{equation} \frac{8}{170}=\frac{4}{85} \end{equation}\)
(iii) (d): Number of \(\begin{equation} ₹ \end{equation} \)10 coins = 28
Probability (coin is of \(\begin{equation} ₹ \end{equation} \)10) = \(\begin{equation} \frac{28}{170} \end{equation}\)
Required probability = 1 - P(coin is of 10)
\(\begin{equation} =1-\frac{28}{170}=\frac{142}{170}=\frac{71}{85} \end{equation}\)
(iv) (a) : Total number of coins of \(\begin{equation} ₹ \end{equation} \)10 and \(\begin{equation} ₹ \end{equation} \) 20
= 28 + 8 = 36
Required probability = \(\begin{equation} \frac{36}{170}=\frac{18}{85} \end{equation}\)
(v) (a): Total number of coins of \(\begin{equation} ₹ \end{equation} \)1, \(\begin{equation} ₹ \end{equation} \)2 and \(\begin{equation} ₹ \end{equation} \) 5
= 50 + 48 + 36 = 134
Required probability = \(\begin{equation} \frac{134}{170}=\frac{67}{85} \end{equation}\) -
Since, every student get one chocolate. So, number of chocolates Rohit has is equal to the number of students in the class.
(i) (a): Let number of milk chocolates Rohit has = x
Probability of distributing milk chocolates = \(\begin{equation} \frac{1}{3} \end{equation}\)
\(\begin{equation} \Rightarrow \frac{x}{54}=\frac{1}{3} \Rightarrow x=\frac{54}{3}=18 \end{equation}\)
(ii) (c): Let number of dark chocolates Rohit has = y
Probability of distributing dark chocolates = \(\begin{equation} \frac{4}{9} \end{equation}\)
\(\begin{equation} \Rightarrow \frac{y}{54}=\frac{4}{9} \Rightarrow y=\frac{4 \times 54}{9}=24 \end{equation}\)
(iii) (d) : Number of white chocolates Rohit has = 54 -(18 + 24) = 12
Required probability = \(\begin{equation} \frac{12}{54}=\frac{2}{9} \end{equation}\)
(iv) (b) : Total number of milk and white chocolates = 18 + 12 = 30
Required probability = \(\begin{equation} \frac{30}{54}=\frac{5}{9} \end{equation}\)
(v) (b): Since all students gets one chocolate. So, total number of chocolates distributed = 54
\(\begin{equation} \text { Required probability }=\frac{54}{54}=1 \end{equation}\) -
Total number of blocks in the kit = 120
Number of red blocks = 40
Number of blue blocks = 25
Number of green blocks = 30
Number of yellow blocks = 120 - (40 + 25 + 30)
= 120 - 95 = 25
(i) (d): P(block is red) \(\begin{equation} =\frac{40}{120}=\frac{1}{3} \end{equation}\)
(ii) (c): P(block is not yellow) = 1 - P(block is yellow)
\(\begin{equation} =1-\frac{25}{120}=1-\frac{5}{24}=\frac{19}{24} \end{equation}\)
(iii) (c) : P(block is green) = \(\begin{equation} \frac{30}{120}=\frac{1}{4} \end{equation}\)
(iv) (b) : P(block is yellow) = \(\begin{equation} \frac{5}{24} \end{equation}\)
(v) (b): P(block is not blue) = 1 - P(block is blue)
\(\begin{equation} =1-\frac{25}{120}=1-\frac{5}{24}=\frac{19}{24} \end{equation}\) -
Total number of fish in the aquarium = 13 + 18 + 12 + 11 = 54
(i) (b): Number of male fish in the aquarium = 36
Number of female fish in the aquarium = 54 - 36 = 18
So, required probability = \(\begin{equation} \frac{18}{54}=\frac{1}{3} \end{equation}\)
(ii) (b): Required probability = \(\begin{equation} \frac{18}{54}=\frac{1}{3} \end{equation}\)
(iii) (d) : P(selecting a koi fish) = \(\begin{equation} \frac{12}{54}=\frac{2}{9} \end{equation}\)
P(not selecting a koi fish) = 1 - P(selecting a koi fish) \(\begin{equation} =1-\frac{2}{9}=\frac{7}{9} \end{equation}\)
(iv) (b) : Total number of guppy fish and koi fish = 13 + 12 = 25
P(selecting neither angel fish nor flowerhorn fish =25/54.
(v) (c): P(selecting a guppy fish) = 13/54. -
(i) (b):Total number of possible outcomes on throwing two dice simultaneously = 6 x 6 = 36
(ii) (c): As we know, that maximum sum of numbers on two dice = 6 + 6 = 12
It is an impossible event.
So, required probability = 0
(iii) (c) : Let A be the event that both the numbers on dice are prime.
A = {(2, 2), (2, 3), (2, 5), (3,2), (3, 3), (3, 5), (5, 2), (5,3), (5, 5)}
\(\Rightarrow\)n(A) = 9
\(\begin{equation} P(A)=\frac{9}{36}=\frac{1}{4} \end{equation}\)
(iv) (c) : Let B the event that product of two numbers is odd.
B = {(1, 1), (1, 3), (1, 5), (3,1), (3, 3), (3, 5), (5,1), (5,3), (5, 5)}
\(\Rightarrow\)n(B) = 9
\(\begin{equation} P(B)=\frac{9}{36}=\frac{1}{4} \end{equation}\)
(v) (c) : Let C be the event that difference of two numbers is zero.
C = {(1, 1), (2,2), (3, 3), (4,4), (5, 5), (6, 6)}
\(\Rightarrow\)n(C) = 6
\(\begin{equation} P(C)=\frac{6}{36}=\frac{1}{6} \end{equation}\) -
Total number of cards left = 52 - (4 + 4 + 4) = 52 - 12 = 40
There are four 2's, four 5's and four Jacks in a deck
(i) (c): P(getting 6 of spade) = \(\begin{equation} \frac{1}{40} \end{equation}\)
(ii) (a): As there is no black diamond in the deck of cards.
P(black diamond) = 0
(iii) (b) : Total number of face cards in a deck = 12
But all Jacks are removed
Number offace cards left = 12 - 4 = 8
So, P(getting a face card) = \(\begin{equation} \frac{8}{40}=\frac{1}{5} \end{equation}\)
(iv) (d) : Number of cards of club left = 13 - 3 = 10
3 cards are removed of each kind
P(getting a club) = \(\begin{equation} \frac{10}{40}=\frac{1}{4} \end{equation}\)
(v) (c): Number of red cards left = 26 - 6 = 20
P(getting a red card) = \(\begin{equation} \frac{20}{40}=\frac{1}{2} \end{equation}\) -
Total number of possible outcomes = 10
(i) (b): P(getting 100% discount) = \(\begin{equation} \frac{1}{10} \end{equation}\)
(ii) (c): P(getting no prize) = \(\begin{equation} \frac{3}{10} \end{equation}\)
(iii) (b) : P(getting a soccer ball) = \(\begin{equation} \frac{2}{10}=\frac{1}{5} \end{equation}\)
(iv) (b) : P(getting 15% discount) = \(\begin{equation} \frac{2}{10}=\frac{1}{5} \end{equation}\)
(v) (a): P(getting a free spin) = \(\begin{equation} \frac{1}{10} \end{equation}\) -
Total number of footballs produced in one day = 220000
(i) (c): P(selecting a defective football) = \(\begin{equation} \frac{15}{100}=\frac{3}{20} \end{equation}\)
(ii) (d): P(selecting a non-defective football) = 1- P(selecting a defective football) = \(\begin{equation} 1-\frac{3}{20}=\frac{17}{20} \end{equation}\)
(iii) (b) : Total number of defective footballs produced in 1 day = \(\begin{equation} \frac{3}{20} \times 22000=3300 \end{equation}\)
(iv) (a) : Total number of non-defective footballs produced in 1 day = 22000 - 3300 = 18700
(v) (d): P(selecting defective football) \(\begin{equation} =\frac{8}{25} \end{equation}\)
P (selecting non-defective football) = \(\begin{equation} 1-\frac{8}{25}=\frac{17}{25} \end{equation}\)
Number of non-defective footballs produced \(\begin{equation} =\frac{17}{25} \times 22000=14960 \end{equation}\) -
Let Band G denotes boy and girl respectively.
Then,
Possible outcomes for Gupta's family having two kids is {BB, BG, GG}
Similarly, possible outcomes for Singhal's family having 3 kids is {BBB, BBG, BGG, GGG}
(i) (b): Required probability = \(\begin{equation} \frac{1}{4} \end{equation}\)
(ii) (b): Required probability = \(\begin{equation} \frac{2}{3} \end{equation}\)
(iii) (b): Required probability = \(\begin{equation} \frac{2}{3} \end{equation}\)
(iv) (b) : Required probability = \(\begin{equation} \frac{1}{4} \end{equation}\)
(v) (c): Required probability = \(\begin{equation} \frac{1}{3}+\frac{1}{4}=\frac{7}{12} \end{equation}\) -
Total number of cartons in the store = 80 + 90 + 38 + 42 = 250
(i) (d) :P(choosing an apple juice carton) = \(\begin{equation} \frac{90}{250}=\frac{9}{25} \end{equation}\)
(ii) (c) : P( choosing an orange juice carton ) = \(\begin{equation} \frac{80}{250}=\frac{8}{25} \end{equation}\)
P(choosing not an orange juice carton) = \(\begin{equation} =1-\frac{8}{25}=\frac{17}{25} \end{equation}\)
(Iii) (d):P(choosing a guava juice carton) = \(\begin{equation} \frac{42}{250}=\frac{21}{125} \end{equation}\)
(iv) (c) : Total number of cartons Vishal bought =4+3+3=10
Number of tetrapacks in 1 carton = 10
Total number of tetrapacks Vishal has = 100
So, P( customer picks a guava juice tetrapack) \(\begin{equation} =\frac{3 \times 10}{100}=\frac{3}{10} \end{equation}\)
(v) (b): Number of cartons left with storekeeper = 250 - 10 = 240
Number of cartons he bought = 14
Total number of cartons are with storekeeper now = 240 + 14 = 254
So, P(selecting a tetrapack of apple juice from store) \(\begin{equation} =\frac{(90-4+14) \times 10}{254 \times 10}=\frac{100}{254}=\frac{50}{127} \end{equation}\) -
Total number of days in June = 30
(i) (c): Number of sunny days = PCsunny day) x 30 = \(\begin{equation} \frac{1}{2} \times 30=15 \end{equation}\)
(ii) (b): Number of cloudy days in June = 5
\(\begin{equation} x=\frac{5}{30}=\frac{1}{6} \end{equation}\)
(iii) (a): Required probability = \(\begin{equation} \frac{1}{2}+\frac{1}{6}+\frac{1}{5}=\frac{13}{15} \end{equation}\)
(iv) (d) : We have, \(\begin{equation} x+y=\frac{3}{10} \Rightarrow y=\frac{3}{10}-\frac{1}{6}=\frac{2}{15} \end{equation}\)
So, number of rainy days = \(\begin{equation} \frac{2}{15} \times 30=4 \end{equation}\)
(v) (c): Number of partially cloudy days = P(partially cloudy days) x 30 \(\begin{equation} =\frac{1}{5} \times 30=6 \end{equation}\)
Case Study Questions

























