CBSE 10th Standard Maths Subject Circles HOT Questions 2 Mark Questions With Solution 2021
By QB365 on 29 May, 2021
QB365 Provides the HOT Question Papers for Class 10 Maths, and also provide the detail solution for each and every HOT Questions. HOT Questions will help to get more idea about question pattern in every exams and also will help to get more marks in Exams
QB365 - Question Bank Software
CBSE 10th Standard Maths Subject Circles HOT Questions 2 Mark Questions With Solution 2021
10th Standard CBSE
-
Reg.No. :
Maths
-
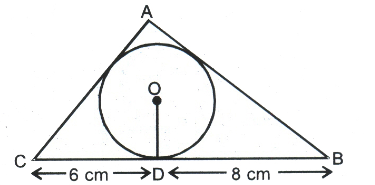
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig). Find the sides AB and AC.
 (a)
(a) -
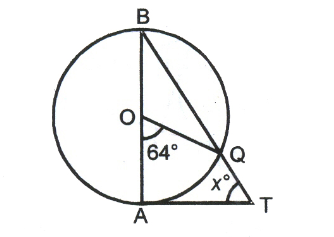
In the given figure, AB is a diameter of the circle, with centre O and AT is a tangent. Calculate the numerical value of x.
 (a)
(a) -
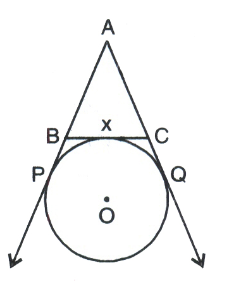
In given figure, find the perimeter of \(\angle ABC\), if AP = 10 cm.
 (a)
(a) -
Two circles intersect each other at two points A and B. From point A, tangents AP and AQ are drawn to two circles which intersect the circles at the pointsP and Q respectively. Prove that AB is the bisector of \(\angle PBQ\).
(a) -
Let A be a point of intersection of two intersecting circles with centres O and O'. The tangents at A to the two circles meet the circles at B and C respectively. Point P is located so that AOPO; is a parallelogram. Prove that P is the circumcentre of \(\triangle ABC\).
(a)
*****************************************
CBSE 10th Standard Maths Subject Circles HOT Questions 2 Mark Questions With Solution 2021 Answer Keys
-
Given, CD = 6 cm, BD = 8 cm and radius = 4 cm
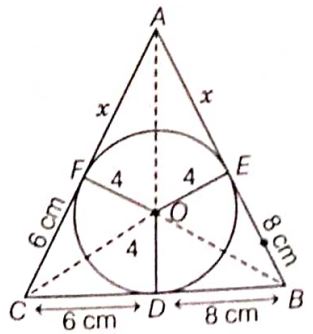
Join OC, OA and OB.
Let the circle touches the other sides AB and AC at points E and F, respectively.
We know that tangents drawn from an external point to the circle are equal in length.
\(\therefore\) CD = CF = 6 cm [\(\because\) C is an external point]
BD = BE = 8 cm [\(\because\) B is an external point]
and AF = AE = x cm (say [\(\because\) A is an external point]
Area of \(\Delta\)OCB, \(A_1=\frac{1}{2} \times \text { Base } \times \text { Height }\)
\(\begin{aligned} & =\frac{1}{2} \times C B \times O D \\ \end{aligned}\)
\(\begin{aligned} & =\frac{1}{2} \times 14 \times 4=28 \mathrm{~cm}^2 \\ \end{aligned}\)
\(\begin{aligned} & \quad[\because C B=C D+B D=6+8=14] \end{aligned}\)
Area of \(\Delta\)OCA,
\(\begin{aligned} A_2 & =\frac{1}{2} \times A C \times O F \end{aligned}\)
\(\begin{aligned} =\frac{1}{2}(6+x) \times 4=(12+2 x) \mathrm{cm}^2 \end{aligned}\)
and area of \(\Delta\)OBA,
\(A_3=\frac{1}{2} \times A B \times O E=\frac{1}{2}(8+x) \times 4=(16+2 x) \mathrm{cm}^2\)
Thus, area of \(\Delta\)ABC
= A1 + A2 + A3 = [28 + (12 + 2x) + (16+ 2x)]
= (56 + 4x) cm2 ...(i)
Now, semi-perimeter of \(\Delta\)ABC=\(\frac{1}{2}\)(AB + BC + CA)
\(\Rightarrow \quad s=\frac{1}{2}(x+8+14+6+x)\)
\(\Rightarrow\) s = (14 + x) cm
Using Heron's formula,
area of \(\Delta\)ABC = \(\begin{aligned} & =\sqrt{s(s-a)(s-b)(s-c)} \end{aligned}\)
\(\begin{aligned} =\sqrt{(14+x)(14+x-14)(14+x-x-6)(14+x-x-8)} \end{aligned}\)
\(\begin{aligned} & =\sqrt{(14+x) \times x \times 8 \times 6} \end{aligned}\)
\(\begin{aligned} =\sqrt{(14+x) 48 x} \end{aligned}\) ...(ii)
From Eqs. (i) and (ii), we get
\(\sqrt{(14+x) 48 x}=56+4 x=4(14+x)\)
On squaring both sides, we get
(14 + x) 48 x = 42 (14 + x)2
\(\Rightarrow\) 3x = 14 + x
\(\Rightarrow\) 2x = 14
\(\Rightarrow\) x = 7
\(\therefore\) Length of AC = 6 + x = 6 + 7 = 13 cm
and length of AB = 8 + x = 8 + 7 = 15 cm -
\(x={ 58 }^{ \circ }\)
-
20 cm
-
Let O and O' be the centres of two circles, tangents AP and AQ intersect these circles in A and the circle with centre O in P and the circle with centre O' in Q. Join PBQ and AB.
-S.png)
Now, AP is a tangent to the circle with centre O' and AB is the chord.
ஃ BAP = AQB .......(i)
[ s in the corresponding alternate segment]
Again, AQ is a tangent to the circle with centre O and AB is the chord.
ஃ \(\angle \)BAQ = \(\angle \)BPA .....(ii)
Now, by angle sum property, we have
\(\angle \)BPA + \(\angle \)BAP + \(\angle \)ABP = 180°
\(\angle \)AQB + \(\angle \)BAQ + \(\angle \)QBA = 180°
FRom (iii) and (iv), we have
\(\angle \)BPA + \(\angle \)BPA + \(\angle \)ABP = \(\angle \)AQB + \(\angle \)BAQ + \(\angle \)QBA
⇒ \(\angle \)ABP = \(\angle \)QBA [using (i) & (ii)]
hence, AB is the bisector of \(\angle \)PBQ. -
Since AB and AC are two tangents from Point A to the two circle.
ஃ OA ⊥ AC and O'A ⊥ AB
[∵ radius through the point of contact is perpendicular to the tangents]
Let OP intersects AB at M, therefore OM ⊥ AB
ஃ AM = BM
[∵ ⊥ from the centre of a circle to a chord bisects the chord]
ஃ OM and hence OP is the perpendicular bisector of AB.
Similarly PO' is perpendicular of AC.
Now, in \(\Delta \)ABC
OP is the perpendicular bisector of side AB.
ஃ PA = PB
[∵ any point on the perpendicular bisector is equidistant from the fixed point]
Similarly, PA = PC
Hence, PA = PB = PC
ஃ P is equidistant from the three vertices of \(\Delta \)ABC.
Hence, P is the circumcentre of \(\Delta \)ABC.
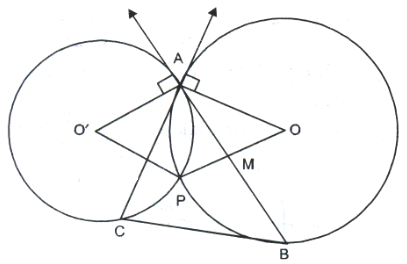
As, AOPO' is a parallelogram.
ஃ AO || O'P [opposite sides of a || gm]
ஃ OP ⊥ AB
[ ∵ AO' || OP and O'A ⊥ AB, ஃ OP ⊥ AB]

























