CBSE 10th Standard Maths Subject Circles Ncert Exemplar 3 Marks Questions 2021
By QB365 on 26 May, 2021
QB365 Provides the updated NCERT Examplar Questions for Class 10 Maths, and also provide the detail solution for each and every ncert examplar questions , QB365 will give all kind of study materials will help to get more marks
QB365 - Question Bank Software
CBSE 10th Standard Maths Subject Circles Ncert Exemplar 3 Marks Questions 2021
10th Standard CBSE
-
Reg.No. :
Maths
-
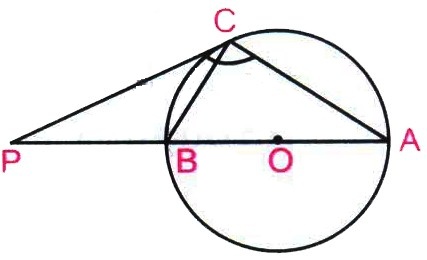
The tangent at a point C of a circle and a diameter AB when extended intersect at P.If \(\angle PCA=110^0\), find \(\angle CBA\) [see figure] Join C with centre O
 (a)
(a) -
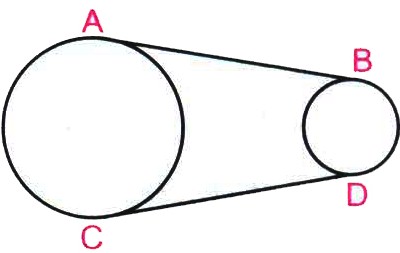
In figure, AB and CD are common tangents to two circles of unequal radii.Prove that AB=CD.
 (a)
(a) -
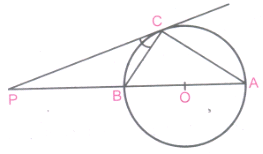
From an external point P, two tangents, PA and PB are drawn to a circle with centre O.At one point E on the circle tangent is drawn which intersect PA and PB at C and D, respectively.If PA = 10cm, find the perimeter of the triangle PCD.
(a) -
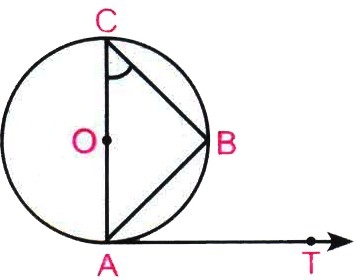
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure.Prove that \(\angle BAT=\angle ACB\)
 (a)
(a) -
AB is a diameter of a circle and AC is its chord such that \(\angle BAC=30°\). If the tangent at C intersects AB extended at D, then prove that BC = BD.
(a)
3 Marks
*****************************************
CBSE 10th Standard Maths Subject Circles Ncert Exemplar 3 Marks Questions 2021 Answer Keys
-
\(\angle \)PCA = 110°
\(\angle \)CBA = ?
\(\angle \)ACB = 90°e [Angle in a semicircle is right agle]
\(\angle \)PCB = 110° - 90° = 20°
\(\angle \)PCB = \(\angle \)CAB = 20° [Alternate segment theorm]
In \(\triangle\)ABC
\(\angle \)ABC + \(\angle \)CAB + \(\angle \)BCA = 180° [∵ Sum of angles of a is 180°]
⇒ \(\angle \)ABC = 180° - 110° = 70° -
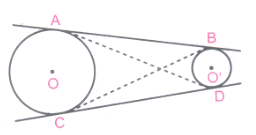
Construction: Join AD and BC
Proof: The tangent drawn from an internal point to a circle are equal in length.
If A is external point for circle hving centre O.
AB = AD .....(i)
If C is external point then
BC = CD .....(ii)
Now, B is external point for circle having centre O
AB = BC .....(iii)
So, from (i), (ii) and (iii), we get
AB = BC = CD
So, AB = CD Hence proved. -
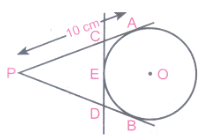
PA= 10 cm.
PA = PB [If P is external point] .....(i)
[ ∵ From an external point tangents drawn to a circle are equal in length]
If C is external point, then CA = CE
If D is external point, then
DB = DE ......(ii)
Perimeter of triangle \(\triangle\)PCD
= PC + CD + PD
= PC + CE + ED + PD
= pc + CA + DB + PD
= PA + PB
-PA + PA = 2 PA
= 2 x 10 = 20 cm.[From (ii)] -
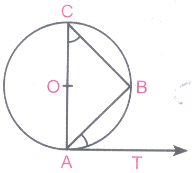
In \(\triangle\)ABC
AC is diameter, B = 90° ......(i)
[In a semicircle there is always a right angle]
So, ACB + CAB = 90°
[∵ sum of angles of a\(\triangle\) is 180°]
OA ⊥ AT [Radius and tangent are ⊥ to each other at the point of contact]
\(\angle \)OAT = 90°
\(\angle \)OAB + \(\angle \)BAT = 90° ......(ii)
From (i) and (ii),
\(\angle \)ACB = \(\angle \)BAT Hence proved. -
\(50\sqrt { 3 } cm^{ 2 }\)
3 Marks

























