CBSE 10th Standard Maths Subject Coordinate Geometry Case Study Questions 2021
By QB365 on 22 May, 2021
QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
CBSE 10th Standard Maths Subject Coordinate Geometry Case Study Questions 2021
10th Standard CBSE
-
Reg.No. :
Maths
-
Alia and Shagun are friends living on the same street in Patel Nagar. Shaguns house is at the intersection of one street with another street on which there is a library. They both study in the same school and that is not far from Shagun's house. Suppose the school is situated at the point 0, i.e., the origin, Alia's house is at A. Shaguns house is at B and library is at C. Based on the above information, answer the following questions.
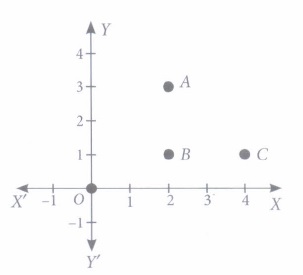
(i) How far is Alia's house from Shaguns house?(a) 3 units (b) 4 units (c) 5 units (d) 2 units (ii) How far is the library from Shaguns house?
(a) 3 units (b) 2 units (c) 5 units (d) 4 units (iii) How far is the library from Alia's house?
(a) 2 units (b) 3 units (c) 4 units (d) (d) None of these (iv) Which of the following is true?
(a) ABC forms a scalene triangle (b) ABC forms an isosceles triangle (c) ABC forms an equilateral triangle (d) None of these (v) How far is the school from Alia's house than Shaguns house?
(a) \(\sqrt(13)\) units (b) \(\sqrt(5)\) units (c) (\(\sqrt(13)\) + \(\sqrt(5)\) )units (d) (\(\sqrt(13)\) - \(\sqrt(5)\) ) units (a) -
A person is riding his bike on a straight road towards East from his college to city A and then to city B. At some point in between city A and city B, he suddenly realises that there is not enough petrol for the journey. Also, there is no petrol pump on the road between these two cities.
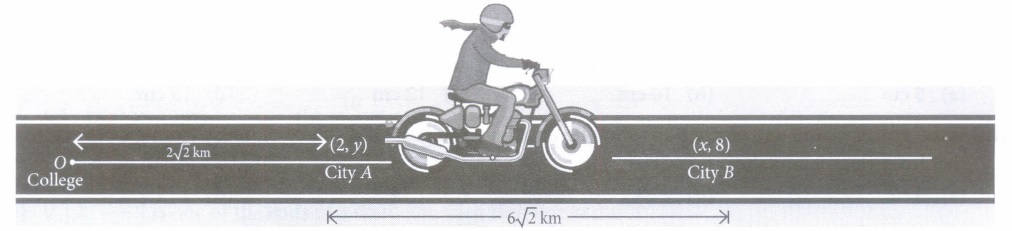
Based on the above information, answer the following questions.
(i) The value of y is equal to(a) 2 (b) 3 (c) 4 (d) 5 (ii) The value of x is equal to
(a) 4 (b) 5 (c) 8 (d) 7 (iii) If M is any point exactly in between city A and city B, then coordinates of M are
(a) 3,3 (b) 4,4 (c) 5,5 (d) 6,6 (iv) The ratio in which A divides the line segment joining the points O and M is
(a) 1:2 (b) 2.1 (c) 3.2 (d) 2.3 (v) If the person analyse the petrol at the point M(the mid point of AB), then what should be his decision?
(a) Should he travel back to college (b) Should try his luck to move towards city B (c) Should be travel back to city A (d) None of these (a) -
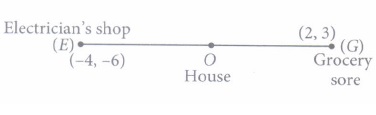
Satellite image of a colony is shown below. In this view, a particular house is pointed out by a flag, which is situated at the point of intersection of x and y-axes. If we go 2 em east and 3 em north from the house, then we reach to a Grocery store. If we go 4 em west and 6 em south from the house, then we reach to a Electrician's shop. If we go 6 em east and 8 em south from the house, then we reach to a food cart. If we go 6 em west and 8 em north from the house, then we reach to a bus stand.
Based on the above information, answer the following questions.
(i) The distance between grocery store and food cart is(a) 12 cm (b) 15 cm (c) 18 cm (d) none of these (ii) The distance of the bus stand from the house is
(a) 5 cm (b) 10 cm (c) 12 cm (d) 15 cm (iii) If the grocery store and electrician's shop lie on a line, the ratio of distance of house from grocery store to that from electrician's shop, is
(a) 3.2 (b) 2.3 (c) 1.2 (d) 2.1 (iv) The ratio of distances of house from bus stand to food cart is
(a) 1.2 (b) 2.1 (c) 1.1 (d) none of these (v) The coordinates of positions of bus stand, grocery store, food cart and electrician's shop form a
(a) rectangle (b) parallelogram (c) square (d) none of these (a) -
A round clock is traced on a graph paper as shown below. The boundary intersect the coordinate axis at a distance of 4/3 units from origin.
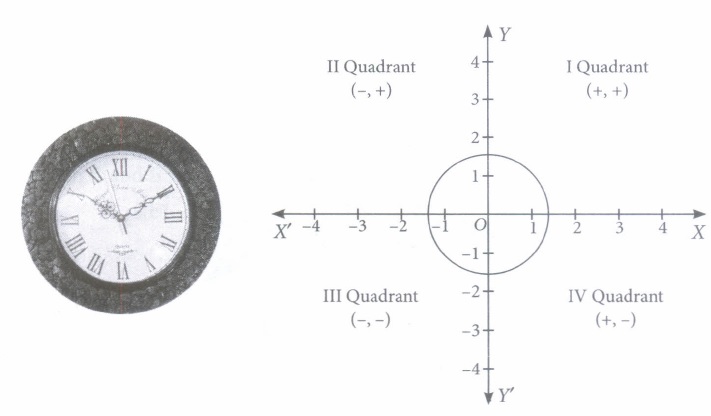
Based on the above information, answer the following questions .
(i) Circle intersect the positive y-axis at\(A\left(\frac{2}{3}, 0\right),\) \((b) \left(0, \frac{2}{3}\right)\) \((c) \left(0, \frac{4}{3}\right)\) \((d) \left(\frac{4}{3}, 0\right)\) (ii) The centre of circle is the
(a) mid-point of points of intersection with x-axis (b) mid-point of points of intersection with y-axis (c) both (a) and (b) (d) none of these (iii) The radius of the circle is
\((a) \frac{4}{3} units\) \((b) \frac{3}{2} units\) \((c) \frac{2}{3} units\) \((d) \frac{3}{4} units\) (iv) The area of the circle is
\((a) 16 \pi^{2} sq. units\) \((b) \frac{16}{9} \pi sq. units\) \((c) \frac{4}{9} \pi^{2} sq. units\) \((d) 4 \pi sq. units\) (v) If \(\left(1, \frac{\sqrt{7}}{3}\right)\) is one of the ends of a diameter, then its other end is
\((a) \left(-1, \frac{\sqrt{7}}{3}\right)\) \((b) \left(1,-\frac{\sqrt{7}}{3}\right)\) \((c) \left(1, \frac{\sqrt{7}}{3}\right)\) \((d) \left(-1,-\frac{\sqrt{7}}{3}\right)\) (a) -
To raise social awareness about hazards of smoking, a school decided to start 'No smoking' campaign. 10 students are asked to prepare campaign banners in the shape of a triangle. The vertices of one of the triangle are P( -3,4), Q(3, 4) and R(-2, -1).

Based on the above information, answer the following questions.
(i) The coordinates of centroid of \(\Delta\)PQR are\((a) \left(\frac{2}{3}, \frac{7}{3}\right)^{n}\) \((b) \left(\frac{1}{3}, \frac{1}{3}\right)\) \((c) \left(\frac{-2}{3}, \frac{7}{3}\right)\) \((d) \left(\frac{7}{3}, \frac{2}{3}\right)\) (ii) If S be the mid-point of line joining P and Q, then coordinates of S are
(a) (4,0) (b) (2,0) (c) (0,2) (d) (0,4) (iii) If T be the mid-point of line joining Rand Q, then coordinates of T are
\((a) \left(\frac{1}{2}, \frac{1}{2}\right)\) \((b) \left(\frac{3}{2}, \frac{1}{2}\right)\) \((c) \left(\frac{1}{2}, \frac{3}{2}\right)\) (d) none of these (iv) If Ube the mid-point of line joining Rand P, then coordinates of U are
\((a) \left(-\frac{5}{2}, \frac{3}{2}\right)\) \((b) \left(\frac{3}{2},-\frac{5}{2}\right)\) \((c) \left(\frac{3}{2}, \frac{5}{2}\right)\) \((d) \left(\frac{5}{2}, \frac{3}{2}\right)\) (v) The coordinates of centroid of \(\Delta\)STU are
\((a) \left(\frac{2}{3}, \frac{7}{3}\right)\) \((b) \left(\frac{1}{3}, \frac{1}{3}\right)\) \((c) \left(-\frac{2}{3}, \frac{7}{3}\right)\) \((d) \left(\frac{7}{3}, \frac{2}{3}\right)\) (a)
Case Study Questions
*****************************************
CBSE 10th Standard Maths Subject Coordinate Geometry Case Study Questions 2021 Answer Keys
-
(i) (d): Since the coordinates of A and Bare (2, 3) and (2, 1) respectively.
\(\therefore\) Required distance = AB
\(=\sqrt{(2-2)^{2}+(1-3)^{2}}=\sqrt{2^{2}}=2 \text { units }\)
(ii) (b): Since, library is situated at C(4, 1)
\(\therefore\)Required distance = BC
\(=\sqrt{(4-2)^{2}+(1-1)^{2}}=\sqrt{2^{2}+0^{2}}=2 \text { units }\)
(iii) (d): Required distance = AC
\(=\sqrt{(4-2)^{2}+(1-3)^{2}}=\sqrt{2^{2}+2^{2}}=2 \sqrt{2} \text { units }\)
(iv) (b): Since AB = BC \(\neq\) AC, therefore \(\Delta\)ABC is an isosceles triangle.
(v) (d): Distance between O and A
\(=\sqrt{2^{2}+3^{2}}=\sqrt{4+9}=\sqrt{13} \text { units }\)
and distance between O and B =
\(\sqrt{2^{2}+1^{2}}=\sqrt{4+1}=\sqrt{5} \text { units }\)
Thus, required distance = \((\sqrt{13}-\sqrt{5}) \text { units }\) -
(i) (a): We have, OA = 2\(\sqrt{2}\) km
\(\Rightarrow \sqrt{2^{2}+y^{2}}=2 \sqrt{2} \)
\(\Rightarrow 4+y^{2}=8 \Rightarrow y^{2}=4 \)
\(\Rightarrow y=2 \quad(\because y=-2 \text { is not possible })\)
(ii) (c): We have OB = 8\(\sqrt{2}\)
\(\Rightarrow \sqrt{x^{2}+8^{2}}=8 \sqrt{2} \)
\(\Rightarrow x^{2}+64=128 \Rightarrow x^{2}=64 \)
\(\Rightarrow x=8 \quad(\because x=-8 \text { is not possible })\)
(iii) (c) : Coordinates of A and Bare (2, 2) and (8, 8) respectively, therefore coordinates of point M are
\(\left(\frac{2+8}{2}, \frac{2+8}{2}\right)\)i.e .,(5.5)
(iv) (d): Let A divides OM in the ratio k: 1.Then
\(2=\frac{5 k+0}{k+1} \Rightarrow 2 \mathrm{k}+2=5 k \Rightarrow 3 k=2 \Rightarrow k=\frac{2}{3}\)
\(\therefore\) Required ratio = 2 : 3
(v) (b): Since M is the mid-point of A and B therefore AM = MB. Hence, he should try his luck moving towards B. -
Consider the house is at origin (0, 0), then coordinates of grocery store, electrician's shop, food cart and bus stand are respectively (2, 3), (-4, -6), (6, - 8) and (-6, 8)
(i) (d): Since, grocery store is at (2, 3) and food cart is at (6, -8)
\(\therefore\) Required distance \(=\sqrt{(6-2)^{2}+(-8-3)^{2}}\)
\(=\sqrt{4^{2}+11^{2}}=\sqrt{16+121}=\sqrt{137} \mathrm{~cm}\)
(ii) (b): Required distance
\(=\sqrt{(-6)^{2}+8^{2}}=\sqrt{36+64}=\sqrt{100}=10 \mathrm{~cm}\)
(iii) (c) : Let 0divides EG in the ratio k : I,then
\(\begin{array}{l} 0=\frac{2 k-4}{k+1} \\ \Rightarrow \quad 2 k=4 \\ \Rightarrow k=2 \end{array}\)
Thus, 0 divides EG in the ratio 2 : 1
Hence, required ratio = OG :OE i.e., 1 : 2
(iv) (c): Since, (0, 0) is the mid-point of (-6,8) and (6, -8), therefore both bus stand and food cart are at equal distances from the house. Hence, required ratio is 1 : 1.
(v) (d): Mid-point of grocery store and electrician's shop is \(\left(\frac{2-4}{2}, \frac{3-6}{2}\right), \text { i.e., }\left(-1, \frac{-3}{2}\right)\) Thus, the diagonals does not bisect each other [\(\because\) Mid-point are not same]
Hence, they form a quadrilateral. -
(i) (c): Required coordinates are \(\left(0, \frac{4}{3}\right)\)
(ii) (c)
(iii) (a): Radius = Distance between (0,0) and \(\left(\frac{4}{3}, 0\right)\)
\(=\sqrt{\left(\frac{4}{3}\right)^{2}+0^{2}}=\frac{4}{3} \text { units }\)
(iv) (b): Area of circle = \(\pi\)(radius)2
\(=\pi\left(\frac{4}{3}\right)^{2}=\frac{16}{9} \pi \text { sq. units }\)
(v) (d): Let the coordinates of the other end be (x,y).
Then (0,0) will bethe mid-point of \(\left(1, \frac{\sqrt{7}}{3}\right)\) and (x, y).
\(\therefore\left(\frac{1+x}{2}, \frac{\frac{\sqrt{7}}{3}+y}{2}\right)=(0,0) \)
\(\Rightarrow \frac{1+x}{2}=0 \text { and } \frac{\frac{\sqrt{7}}{3}+y}{2}=0 \)
\(\Rightarrow x=-1 \text { and } y=-\frac{\sqrt{7}}{3}\)
Thus, the coordinates of other end be \(\left(-1, \frac{-\sqrt{7}}{3}\right)\) -
(i) (c): We have, P( -3,4), Q(3, 4) and R( -2, -1).
\(\therefore\) Coordinates of centroid of \(\Delta\)PQR
\(=\left(\frac{-3+3-2}{3}, \frac{4+4-1}{3}\right)=\left(\frac{-2}{3}, \frac{7}{3}\right)\)
(ii) (d): Coordinates of S= \(\left(\frac{-3+3}{2}, \frac{4+4}{2}\right)=(0,4)\)
(iii) (c): Coordinates of T= \(\left(\frac{-2+3}{2}, \frac{-1+4}{2}\right)=\left(\frac{1}{2}, \frac{3}{2}\right)\)
(iv) (a): Coordinates of U = \(\left(\frac{-2-3}{2}, \frac{-1+4}{2}\right)=\left(\frac{-5}{2}, \frac{3}{2}\right)\)
(v) (c): The centroid of triangle formed by joining the mid-points of sides of given triangle is same as that of the given trangle.
So, centroid of \(\Delta S T U=\left(\frac{-2}{3}, \frac{7}{3}\right)\)
Case Study Questions

























