CBSE 10th Standard Maths Subject HOT Questions 3 Mark Questions With Solution 2021
By QB365 on 29 May, 2021
QB365 Provides the HOT Question Papers for Class 10 Maths, and also provide the detail solution for each and every HOT Questions. HOT Questions will help to get more idea about question pattern in every exams and also will help to get more marks in Exams
QB365 - Question Bank Software
CBSE 10th Standard Maths Subject HOT Questions 3 Mark Questions With Solution 2021
10th Standard CBSE
-
Reg.No. :
Maths
-
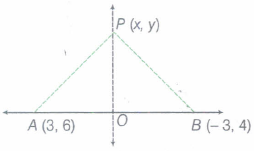
Find the equation of the perpendicular bisector of AB, where A and B are the points (3, 6) and (-3, 4). respectively. Also, find its point of intersection with
(i) X-axis
(ii) Y-axis.(a) -
Find the coordinates of the circumcenter of the triangle whose vertices are (8,6), (8,- 2) and (2, - 2).Also, find its circumradius.
(a) -
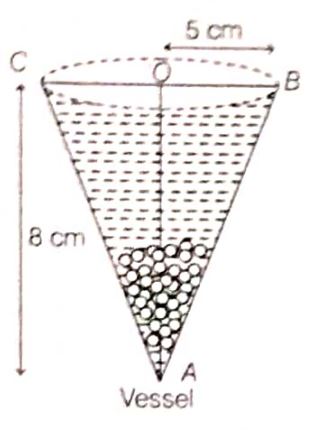
A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one- fourth of the water flows out. Find the number of lead shots dropped in the vessel.
 (a)
(a) -
How many metres of cloth 1.1 m wide will be required to make a conical tent, whose vertical height is 12 m and base radius is 16 m ? Find also the cost of the cloth used at the rate of Rs. 14 per metre.
(a)
*****************************************
CBSE 10th Standard Maths Subject HOT Questions 3 Mark Questions With Solution 2021 Answer Keys
-
Let P (x, y) be any point on the perpendicular bisector of AB.
Then, PA =PB
\(\Rightarrow \ \sqrt { { \left( x-3 \right) }^{ 2 }+{ \left( y-6 \right) }^{ 2 } } =\sqrt { { \left( x+3 \right) }^{ 2 }+{ \left( y-4 \right) }^{ 2 } } \) [\(\because \) distance=\(\sqrt { { \left( { x }_{ 2 }-{ x }_{ 1 } \right) }^{ 2 }-{ \left( { y }_{ 2 }-{ y }_{ 1 } \right) }^{ 2 } } \)]
On squaring both sides, we get \({ \left( x-3 \right) }^{ 2 }+{ \left( y-6 \right) }^{ 2 }={ \left( x+3 \right) }^{ 2 }+{ \left( y-4 \right) }^{ 2 }\)
\(\Rightarrow \) x2-6x+9+y2-12y+36 = x2+6x+9+y2 -8y+16
\(\Rightarrow \)12x+4y-20=0
\(\Rightarrow\) 3x+y-5 = 0 [dividing by 4] ......(i)
Hence, the equation of the perpendicular bisector of AB is 3x + Y - 5 = O.
(i) We know that y-coordinate of every point on X-axis is zero.
On putting y = 0 in Eq. (i), we get
3x - 5 = 0 \(\Rightarrow\) \(x=\frac { 5 }{ 3 } \)
Thus, the perpendicular bisector of AB cuts X-axis at \(\left( \frac { 5 }{ 3 } ,0 \right) \)
(ii) The coordinates of any point on Y-axis are of the form (0, y).
On putting x = 0 in Eq. (i), we get
y-5=0 \(\Rightarrow \) y = 5
Thus, the perpendicular bisector of AB intersects Y-axis at (0, 5). -
We know that the circumcentre of a triangle is equidistant from the vertices of a triangle.Let A (8,6), B (8, - 2) and C (2, - 2) be the vertices of the given triangle
and P(x, Y) be the circumcentre of this triangle.
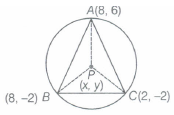
Then, PA = PB = PC [radii of circle]
\(\Rightarrow \) PA2 = PB2 =PC2
Now, PA2 = PB2
\(\Rightarrow \) (x-8)2+(y-6)2 = (x-8)2+(y+2)2 [\(\because \) distance=\(\sqrt { { \left( { x }_{ 2 }-{ x }_{ 1 } \right) }^{ 2 }-{ \left( { y }_{ 2 }-{ y }_{ 1 } \right) }^{ 2 } } \)]
\(\Rightarrow \) x2-16x+64+y2-12y+36 = x2-16x+64+y2+4y+4
\(\Rightarrow \)-12y-4y=4-36 \(\Rightarrow \) 16y=32
\(\therefore \) y=2 and PB2 =PC2
\(\Rightarrow \)(x-8)2+(y+2)2 = (x-2)2+(y+2)2
\(\Rightarrow \)x2-16x+64+y2+4y+4 = x2-4x+4+y2+4y+4
\(\Rightarrow \) -16x+4x=8-68
\(\Rightarrow \)12x=60
\(\therefore \) x=5
So, the coordinates of the circumcenter Pare (5, 2).
Also, circum radius, PA = PB = PC
=\(\sqrt { { \left( 5-8 \right) }^{ 2 }+{ \left( 2-6 \right) }^{ 2 } } =\sqrt { { \left( -3 \right) }^{ 2 }+{ \left( -4 \right) }^{ 2 } } \)
=\(\sqrt { 9+16 } =\sqrt { 25 } =5\) units
Hence, circumradius of the circle is 5 units. -
Here, a cone and spherical lead shots are given. Since, lead shots are dropped into the vessel, so the water which flows out from the vessel is equal to the volume of lead shots.
Given, height of the vessel, h = 8 cm and radius of the vessel, r = 5 cm.
\(\therefore\) Volume of water filled in a vessel = Volume of cone
\(\begin{aligned} & =\frac{1}{3} \times \pi \times r^2 \times h \\ \end{aligned}\)
\(\begin{aligned} & =\frac{1}{3} \times \frac{22}{7} \times 5 \times 5 \times 8 \\ \end{aligned}\)
\(\begin{aligned} & =\frac{4400}{21} \mathrm{~cm}^3 \end{aligned}\)
Also, radius of a spherical lead shot = 0.5 cm
\(\therefore\) Volume of one spherical lead shot \(=\frac{4}{3} \times \pi \times r^3\)
\(=\frac{4}{3} \times \frac{22}{7} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{11}{21} \mathrm{~cm}^3\)
Let n be the number of lead shots dropped in the vessel, then according to the question,
n \(\times\) Volume of one spherical lead shot
= \(\frac{1}{4}\)\(\times\)Volume of water filled in a vessel
\(\begin{aligned} \Rightarrow & & n \times \frac{11}{21} & =\frac{4400}{21} \times \frac{1}{4} \\ \end{aligned}\)
\(\begin{aligned} \Rightarrow & & n \times 11 & =1100 \\ \end{aligned}\)
\(\begin{aligned} \Rightarrow & & n & =100 \end{aligned}\)
Hence, required number of lead shots is 100. -
914.29 m, Rs. 12800.06

























