CBSE 10th Standard Maths Subject HOT Questions 4 Mark Questions With Solution 2021
By QB365 on 29 May, 2021
QB365 Provides the HOT Question Papers for Class 10 Maths, and also provide the detail solution for each and every HOT Questions. HOT Questions will help to get more idea about question pattern in every exams and also will help to get more marks in Exams
QB365 - Question Bank Software
CBSE 10th Standard Maths Subject HOT Questions 4 Mark Questions With Solution 2021
10th Standard CBSE
-
Reg.No. :
Maths
-
A pole 5m high is fixed on the top of a tower. The angle of elevation of the top of the pole observed from a point A on the ground is 600 and the angle of depression of the point A from the top of the tower is 45o . Find the height of the tower.
(a) -
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see the fig). Find the length TP.
(a) -
In a musical chair game, the person playing the music has been advised to stop playing the music at any time within 2 minutes after she starts playing. What is the probability that the music will stop within the first half-minute after starting?
(a)
*****************************************
CBSE 10th Standard Maths Subject HOT Questions 4 Mark Questions With Solution 2021 Answer Keys
-
6.83m
-
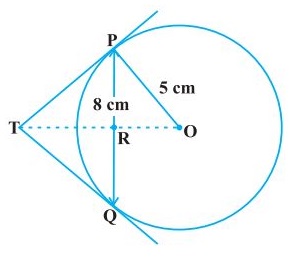
Join OT. Let it intersect PQ at the point R. Then \(\Delta\) TPQ is isosceles and TO is the angle bisector of \(\angle\) PTQ. So, OT \(\perp\) PQ and therefore, OT bisects PQ which gives PR = RQ = 4 cm.
Also, \(\mathrm{OR}=\sqrt{\mathrm{OP}^{2}-\mathrm{PR}^{2}}=\sqrt{5^{2}-4^{2}} \mathrm{~cm}=3 \mathrm{~cm}\)
Now, \(\angle \mathrm{TPR}+\angle \mathrm{RPO}=90^{\circ}=\angle \mathrm{TPR}+\angle \mathrm{PTR}\)
So, \(\angle \mathrm{RPO}=\angle \mathrm{PTR}\)
Therefore, right triangle TRP is similar to the right triangle PRO by AA similarity
This gives \(\frac{\mathrm{TP}}{\mathrm{PO}}=\frac{\mathrm{RP}}{\mathrm{RO}}, \text { i.e., } \frac{\mathrm{TP}}{5}=\frac{4}{3} \text { or } \mathrm{TP}=\frac{20}{3} \mathrm{~cm}\)
Note : TP can also be found by using the Pythagoras Theorem, as follows:
Let TP = x and TR = y. Then
x2 = y2 + 16 (Taking right \(\Delta PRT\) ) (1)
x2 + 52 = (y + 3)2(Taking right \(\Delta \mathrm{OPT}\) ) (2)
Subtracting (1) from (2), we get
\(25=6 y-7 \quad \text { or } \quad y=\frac{32}{6}=\frac{16}{3}\)
Therefore, \(x^{2}=\left(\frac{16}{3}\right)^{2}+16=\frac{16}{9}(16+9)=\frac{16 \times 25}{9}\) [From (1)]
or \(x=\frac{20}{3}\) -
Here the possible outcomes are all the numbers between 0 and 2. This is the portion of the number line from 0 to 2.

Let E be the event that ‘the music is stopped within the first half-minute’.
The outcomes favourable to E are points on the number line from 0 to \(\frac{1}{2}\).
The distance from 0 to 2 is 2, while the distance from 0 to \(\frac{1}{2}\) is \(\frac{1}{2}\).
Since all the outcomes are equally likely, we can argue that, of the total distance of 2, the distance favourable to the event E is \(\frac{1}{2}\).
So, \(\mathrm{P}(\mathrm{E})=\frac{\text { Distance favourable to the event } \mathrm{E}}{\text { Total distance in which outcomes can lie }}=\frac{\frac{1}{2}}{2}=\frac{1}{4}\)

























